Une Symphonie Mathématique au Cœur de l’Électromagnétisme

31 mars 2024 Math, Physique

La Quête d’Unification

L’histoire de l’électromagnétisme est une saga fascinante de découverte et d’innovation, illustrant la quête incessante de l’humanité pour comprendre les forces fondamentales de la nature. Cette quête a culminé avec les travaux de James Clerk Maxwell au XIXe siècle, unifiant les théories de l’électricité, du magnétisme et de la lumière dans un cadre mathématique cohérent.

Les prémices historiques de l’électromagnétisme

L’aventure de l’électromagnétisme débute bien avant Maxwell, avec des expériences rudimentaires sur l’électricité statique et le magnétisme. Des figures comme Coulomb, Ampère, et Faraday ont jeté les bases de ce qui allait devenir l’électromagnétisme, à travers leurs découvertes des lois régissant les charges électriques et les champs magnétiques.

James Clerk Maxwell : Biographie d’un visionnaire

James Clerk Maxwell, né en 1831 en Écosse, était un physicien et mathématicien prodige. Son intérêt pour les sciences s’est manifesté dès son plus jeune âge, le conduisant à approfondir les travaux de ses prédécesseurs. Sa contribution la plus remarquable fut la formulation des équations qui portent aujourd’hui son nom, établissant un pont entre les observations expérimentales de Faraday et un formalisme mathématique rigoureux.

Les travaux précurseurs dans le domaine de l’électricité et du magnétisme ont posé des questions cruciales, mais c’est Maxwell qui a apporté les réponses. En s’appuyant sur les concepts de champ électrique et magnétique introduits par Faraday, il a été le premier à proposer une théorie unifiée des phénomènes électromagnétiques, révolutionnant notre compréhension de la nature.

La beauté de l’approche de Maxwell réside dans son utilisation de la mathématique comme outil pour exprimer et prédire les interactions entre l’électricité et le magnétisme. En formulant ses célèbres équations, Maxwell n’a pas seulement unifié des domaines auparavant distincts de la physique, mais il a également jeté les bases pour le développement futur de technologies qui ont transformé le monde, telles que la radio, la télévision, et bien au-delà.

En résumé, la quête d’unification de l’électromagnétisme, menée par des générations de scientifiques, trouve son apogée dans les travaux de Maxwell. Ces travaux ne sont pas seulement un triomphe de l’intellect humain; ils sont aussi une démonstration puissante de la capacité des mathématiques à révéler les lois cachées de l’univers.

Fondements Mathématiques des Équations de Maxwell

Les équations de Maxwell ne sont pas simplement le fruit d’une intuition physique ; elles reposent sur un socle mathématique solide, tirant parti de concepts avancés pour modéliser les phénomènes électromagnétiques. Ce chapitre explore les lois fondamentales de l’électromagnétisme et l’introduction des nombres complexes, qui jouent un rôle clé dans la manipulation des équations de Maxwell.

De Faraday à Maxwell : Les lois de l’électromagnétisme

Pour comprendre les équations de Maxwell, il est essentiel de commencer par les lois physiques qui les sous-tendent. Ces lois incluent :

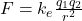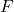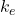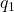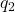  • La loi de Coulomb, qui décrit la force électrostatique agissant entre deux charges ponctuelles : F = k_e \frac{q_1 q_2}{r^2}, où F est la force entre les charges, k_e est la constante électrostatique, q_1 et q_2 sont les valeurs des charges, et r est la distance qui les sépare.
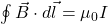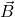  • La loi d’Ampère, qui relie le champ magnétique circulant autour d’un courant électrique à l’intensité de ce courant : \oint \vec{B} \cdot d\vec{l} = \mu_0 I, où \vec{B} est le champ magnétique, 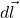d\vec{l} est un élément différentiel du chemin d’intégration, 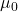\mu_0 est la perméabilité du vide, et 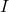I est le courant électrique.
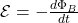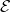  • La loi de Faraday de l’induction électromagnétique, qui établit qu’un changement dans le flux magnétique à travers une surface induit une tension électrique dans un circuit : \mathcal{E} = -\frac{d\Phi_B}{dt}, où \mathcal{E} est la force électromotrice induite et 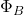\Phi_B est le flux magnétique.

Ces lois, ainsi que d’autres observations et expériences, ont fourni à Maxwell le cadre nécessaire pour développer ses équations.

Introduction aux nombres complexes et à leur rôle en physique

Les nombres complexes, sous la forme a + bi, où a et b sont des nombres réels et i est l’unité imaginaire satisfaisant i^2 = -1, sont cruciaux pour résoudre de nombreux problèmes d’électromagnétisme. Leur capacité à représenter simultanément amplitude et phase rend les équations impliquant des ondes électromagnétiques beaucoup plus maniables.

Maxwell a utilisé ces outils mathématiques, en particulier le calcul différentiel et intégral, pour formaliser ses idées. Les nombres complexes, en tant que partie intégrante de cette boîte à outils, permettent de simplifier les équations de propagation des ondes et de résoudre des problèmes d’électromagnétisme dynamique avec une élégance et une efficacité remarquables.

En résumé, les fondements mathématiques des équations de Maxwell englobent une maîtrise de la physique classique et des outils mathématiques avancés, dont les nombres complexes. Ces outils ne se contentent pas de fournir des solutions ; ils offrent une nouvelle perspective sur la nature de l’électromagnétisme, révélant la structure sous-jacente des phénomènes physiques.

Les Équations de Maxwell Dévoilées

Au cœur de la théorie de l’électromagnétisme de Maxwell se trouvent quatre équations élégantes qui ont transformé notre compréhension des phénomènes électriques et magnétiques. Ces équations décrivent comment les champs électriques et magnétiques se propagent, interagissent, et sont influencés par les charges et les courants. Ce chapitre examine la formulation et l’interprétation physique de ces équations révolutionnaires.

Formulation initiale et interprétations physiques

Les équations de Maxwell peuvent être exprimées dans le vide (absence de charges et de courants) ou en présence de matière (charges et courants présents). Voici leurs formes dans le vide, utilisant le système d’unités SI :

  1. Loi de Gauss pour l’électricité : La divergence d’un champ électrique est proportionnelle à la densité de charge locale.
    \nabla \cdot \vec{E} = \frac{\rho}{\varepsilon_0}
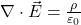
  2. Loi de Gauss pour le magnétisme : Les champs magnétiques n’ont ni source ni puits ; les lignes de champ forment des boucles fermées.
    \nabla \cdot \vec{B} = 0
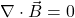
  3. Loi de Faraday de l’induction : Un champ magnétique variable dans le temps crée un champ électrique circulaire.
    \nabla \times \vec{E} = -\frac{\partial \vec{B}}{\partial t}
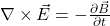
  4. Loi d’Ampère-Maxwell : Un champ électrique variable dans le temps génère un champ magnétique, en plus du champ magnétique produit par le courant électrique.
    \nabla \times \vec{B} = \mu_0\vec{J} + \mu_0\varepsilon_0\frac{\partial \vec{E}}{\partial t}

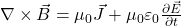
Analyse mathématique des équations : Différentielles et solutions

Les équations de Maxwell sont formulées en termes d’équations différentielles partielles (EDP), un domaine des mathématiques spécialisé dans les fonctions multivariées et leurs taux de variation. La beauté et la complexité des EDP résident dans leur capacité à modéliser des phénomènes variés dans le temps et l’espace, rendant les équations de Maxwell particulièrement puissantes pour décrire la dynamique des champs électriques et magnétiques.

La résolution des équations de Maxwell nécessite une compréhension approfondie du calcul vectoriel et des techniques mathématiques avancées, telles que les méthodes numériques pour les systèmes non linéaires. Les solutions des équations de Maxwell révèlent la nature ondulatoire de l’électromagnétisme et ont conduit à la prédiction et à la découverte de phénomènes tels que les ondes électromagnétiques, y compris la lumière visible.

Ces équations ont également mis en évidence le lien profond entre l’électricité et le magnétisme, montrant qu’ils ne sont pas des phénomènes distincts mais plutôt deux aspects d’une même force fondamentale. Cette unification a ouvert la voie à de nouvelles théories et technologies qui ont révolutionné la société moderne.

Applications et Conséquences des Équations de Maxwell

Les équations de Maxwell ne se contentent pas de décrire théoriquement les interactions électromagnétiques ; elles sont également au cœur de nombreuses technologies modernes et ont ouvert de nouveaux champs de recherche en physique. Ce chapitre se penche sur quelques-unes des applications les plus marquantes de ces équations et sur leur impact durable sur la science et la technologie.

De la lumière aux ondes électromagnétiques : Unification et découvertes

La prédiction la plus spectaculaire issue des équations de Maxwell est que la lumière est une forme d’onde électromagnétique. Cette révélation a non seulement unifié les champs de l’optique, de l’électricité, et du magnétisme sous un même cadre théorique, mais a aussi ouvert la voie à la découverte d’autres ondes électromagnétiques, telles que les rayons X, les ondes radio, et les micro-ondes.

La capacité de générer et de contrôler ces ondes a eu des implications révolutionnaires, allant de la communication sans fil (radio, télévision, téléphones portables) à la médecine (imagerie par rayons X, IRM) et à la navigation (radar).

Impact sur la technologie moderne : Communications, électrotechnique, et au-delà

Les équations de Maxwell sont fondamentales dans la conception et l’analyse des systèmes électriques et de communication. Elles permettent aux ingénieurs de concevoir des antennes, des guides d’ondes, des fibres optiques, et d’autres dispositifs clés qui forment l’épine dorsale de nos infrastructures de communication.

En électrotechnique, la compréhension des champs électromagnétiques a conduit au développement de moteurs électriques, de générateurs, et de transformateurs, qui sont essentiels à la production et à la distribution de l’énergie électrique.

Au-delà de l’Électromagnétisme : Les Équations de Maxwell et la Relativité

L’impact des équations de Maxwell dépasse le cadre de l’électromagnétisme. Elles ont joué un rôle crucial dans le développement de la théorie de la relativité restreinte par Albert Einstein. La constance de la vitesse de la lumière dans tous les référentiels d’inertie, un postulat central de la relativité, découle directement des équations de Maxwell. Cette théorie a profondément modifié notre compréhension de l’espace, du temps, et de la gravité.

Les équations de Maxwell ont également inspiré des recherches en mécanique quantique et dans la recherche de la théorie du tout, tentant d’unifier toutes les forces fondamentales de la nature.

Nombres Complexes en Électromagnétisme : Outil de Résolution et d’Analyse

L’introduction des nombres complexes dans l’étude de l’électromagnétisme représente un tournant dans la manière dont les scientifiques et les ingénieurs comprennent et manipulent les équations de Maxwell. Ce chapitre souligne l’importance de ces outils mathématiques dans la simplification des calculs impliquant des ondes électromagnétiques.

Manipulation des ondes via les nombres complexes

Les nombres complexes facilitent grandement l’analyse des phénomènes oscillatoires, comme les ondes électromagnétiques. En représentant une onde comme une fonction exponentielle complexe, e^{i\omega t} (où i est l’unité imaginaire et \omega est la fréquence angulaire), les physiciens peuvent utiliser les propriétés algébriques des nombres complexes pour simplifier la description des ondes se propageant dans l’espace et le temps.

Cette approche permet de décomposer facilement les signaux en leurs composantes de fréquence (analyse de Fourier), un concept clé dans la conception des systèmes de communication et dans l’analyse des propriétés de matériaux à différentes échelles.

Cas pratiques : Résolution des équations de Maxwell dans différents contextes

Dans la pratique, l’utilisation des nombres complexes se révèle indispensable pour résoudre les équations de Maxwell dans des situations variées, telles que :

  • Propagation d’ondes dans le vide ou dans des milieux matériaux : Les nombres complexes aident à exprimer les solutions des équations de Maxwell sous forme d’ondes se propageant avec une certaine amplitude et phase, facilitant ainsi l’étude de la réflexion, de la réfraction, et de l’absorption des ondes électromagnétiques par différents matériaux.
  • Circuits RLC en régime sinusoïdal : Dans l’analyse des circuits électriques oscillants, les nombres complexes permettent de traiter facilement les impédances des résistances, des inductances et des capacités, offrant une méthode élégante pour résoudre ces circuits.
  • Électrodynamique quantique : Bien au-delà de l’électromagnétisme classique, les nombres complexes jouent un rôle central dans la description des interactions entre la lumière et la matière à l’échelle quantique, montrant une fois de plus l’universalité de cet outil mathématique.

Au-delà de l’Électromagnétisme : Les Équations de Maxwell et la Relativité

L’influence des équations de Maxwell s’étend bien au-delà des frontières de l’électromagnétisme, jouant un rôle crucial dans le développement de la théorie de la relativité restreinte. Ce chapitre explore cette connexion profonde et examine comment les idées de Maxwell ont ouvert la voie à une nouvelle compréhension de l’univers.

Influence sur la théorie de la relativité d’Einstein

L’un des résultats les plus surprenants des équations de Maxwell est que la vitesse de la lumière dans le vide est constante et indépendante du mouvement de la source ou de l’observateur. Cette conclusion, en apparence innocente, a des implications profondes pour notre compréhension de l’espace et du temps.

Albert Einstein a saisi l’importance de cette constance dans ses équations de Maxwell pour formuler sa théorie de la relativité restreinte en 1905. Il postule que les lois de la physique sont les mêmes dans tous les référentiels inertiels et que la vitesse de la lumière dans le vide est la même pour tous les observateurs, quelle que soit leur vitesse relative.

Ces idées ont conduit à des concepts révolutionnaires, tels que la dilatation du temps et la contraction des longueurs, qui ont été vérifiés expérimentalement depuis. La relativité restreinte a également modifié notre compréhension de la masse et de l’énergie, établissant leur équivalence à travers la célèbre équation E=mc^2.

Implications philosophiques et physiques de l’interconnexion entre lumière, espace, et temps

Les travaux de Maxwell, en montrant que la lumière est une onde électromagnétique, et ceux d’Einstein, en explorant les conséquences de cette réalité à l’échelle cosmique, ont non seulement bouleversé la physique mais ont aussi eu un impact profond sur la philosophie et notre vision du monde.

Cette interconnexion entre lumière, espace et temps soulève des questions fondamentales sur la nature de l’univers, notre place en son sein, et la manière dont nous percevons la réalité. Elle a inspiré des générations de scientifiques et de penseurs à reconsidérer ce que nous tenons pour acquis et à explorer les limites de notre compréhension.

Conclusion : L’Héritage des Équations de Maxwell dans les Sciences Modernes

L’aventure à travers les équations de Maxwell nous a menés de leurs fondations mathématiques et physiques à leurs applications vastes et variées, démontrant leur rôle central non seulement en électromagnétisme mais aussi dans le développement de théories physiques fondamentales telles que la relativité. Ces équations constituent une des plus grandes réalisations de l’intellect humain, illustrant la puissance de la pensée abstraite pour décrypter les mystères de l’univers.

Récapitulatif de l’impact transdisciplinaire

Les équations de Maxwell ne sont pas seulement une pierre angulaire de l’électromagnétisme; elles sont aussi un exemple brillant de la manière dont les mathématiques peuvent être utilisées pour formuler des lois physiques universelles. Leur application a transformé de nombreux domaines, de la technologie des communications à la physique théorique, et continue d’inspirer des avancées dans des domaines aussi divers que la mécanique quantique, l’ingénierie électrique, et au-delà.

Les équations de Maxwell : Une inspiration continue pour les mathématiciens et physiciens

L’héritage des équations de Maxwell dépasse leur contribution scientifique directe. Elles représentent un modèle d’unification des forces naturelles qui inspire encore aujourd’hui la recherche d’une théorie du tout. De plus, l’élégance et la simplicité de ces équations rappellent que derrière les phénomènes physiques les plus complexes se cachent souvent des principes d’une beauté mathématique stupéfiante.

Le voyage de Maxwell, de la curiosité intellectuelle à la découverte révolutionnaire, est un témoignage de la quête humaine de connaissance. Ses équations nous rappellent que l’exploration scientifique, guidée par la rigueur mathématique et l’imagination créative, a le pouvoir de révéler les secrets les plus profonds de notre monde.

Check Also

Les « Obelisks » et les Axions : Entre Microbiome et Étoiles à Neutrons

Introduction : Une histoire de viroïdes et de mystères cosmiques Imaginez des éléments minuscules qui …

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *

© EYELO 2024, tout droit réservé