On a tous eu ce moment où l’on regarde notre montre et où l’on se dit, « Comment ça marche exactement, ce truc ? » C’est un peu comme ouvrir un livre de physique quantique pour la première fois : on voit des concepts complexes, des rouages, des ressorts, et on ne comprend pas comment tout ça peut tenir ensemble (et encore moins nous donner l’heure !). Mais derrière ce simple « tic-tac » se cache une mécanique sophistiquée, presque magique, qui parvient à mesurer le temps avec une précision incroyable.
Ce qui est fascinant, c’est qu’une montre mécanique repose sur les principes fondamentaux de la physique classique. C’est comme avoir une petite leçon de mécanique dans sa poche, sauf qu’au lieu de formules sur un tableau, on a des ressorts tendus et des engrenages qui se refilent l’énergie comme des étudiants en plein examen.
Dans cet article, on va plonger au cœur de la mécanique horlogère, pour découvrir comment un ressort nerveux, un échappement anarchiste, un balancier discipliné et des engrenages procrastinateurs collaborent pour transformer l’énergie stockée en un mouvement précis des aiguilles. Préparez-vous à être émerveillé(e) par la physique cachée derrière chaque « tic-tac » !
Le Ressort, cette boule de nerfs prête à tout casser
Pour commencer notre exploration de l’univers complexe d’une montre mécanique, plongeons dans la source première de toute cette mécanique sophistiquée : le ressort moteur. Ce composant essentiel est un peu comme l’étudiant avant un gros examen : tendu et plein d’énergie potentielle. La différence, c’est que le ressort, lui, libère son énergie de manière plus maîtrisée (enfin, la plupart du temps…)
Comprendre l’énergie stockée
Le ressort moteur d’une montre mécanique est essentiellement un ressort spiralé, qui lorsqu’il est tendu, stocke de l’énergie potentielle élastique. Mathématiquement, on peut modéliser un tel ressort comme un ressort de torsion, où l’énergie potentielle élastique est donnée par la relation suivante :
![]()
Dans cette formule :
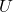 représente l’énergie potentielle élastique en joules (J).
représente l’énergie potentielle élastique en joules (J).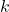 est la constante de torsion du ressort, exprimée en N.m/rad.
est la constante de torsion du ressort, exprimée en N.m/rad.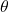 est l’angle de déformation (en radians) par rapport à la position d’équilibre.
est l’angle de déformation (en radians) par rapport à la position d’équilibre.
La valeur de ![]() dépend de la rigidité du ressort, de sa géométrie et de son matériau. Ce paramètre est crucial car il détermine la capacité du ressort à stocker de l’énergie élastique et donc à alimenter toute la montre.
dépend de la rigidité du ressort, de sa géométrie et de son matériau. Ce paramètre est crucial car il détermine la capacité du ressort à stocker de l’énergie élastique et donc à alimenter toute la montre.
Le couple exercé par le ressort
En plus de stocker de l’énergie, le ressort exerce un couple proportionnel à sa déformation angulaire, selon la relation suivante :
![]()
où :
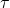 est le couple exercé par le ressort (en N.m).
est le couple exercé par le ressort (en N.m).
Ce couple est transféré à un barillet, qui convertit cette énergie élastique en une énergie cinétique de rotation. À ce stade, l’essentiel est de comprendre que plus le ressort est tendu, plus le couple est important, ce qui nous amène à une petite analogie amusante : c’est un peu comme le stress d’un étudiant qui monte à l’approche des examens — sauf que dans le cas du ressort, ce stress est efficacement canalisé.
Les limites de l’énergie stockée et la relation non-linéaire
On peut se demander si on peut simplement tendre le ressort à l’infini pour obtenir plus d’énergie. La réponse est bien sûr non, car au-delà d’un certain point, le ressort se déformerait de manière plastique et perdrait ses propriétés élastiques. C’est ce qu’on appelle la limite élastique du ressort.
Si on pousse les calculs un peu plus loin, la non-linéarité intervient lorsque la déformation dépasse certaines limites, rendant la relation ![]() inexacte. Une modélisation plus poussée pourrait inclure des termes non-linéaires pour décrire le comportement élastique au-delà de l’élasticité linéaire :
inexacte. Une modélisation plus poussée pourrait inclure des termes non-linéaires pour décrire le comportement élastique au-delà de l’élasticité linéaire :
![]()
où ![]() représente un facteur de non-linéarité. Bien que cette relation plus complexe soit rarement utilisée dans les montres de tous les jours, elle souligne la sophistication potentielle de la mécanique élastique.
représente un facteur de non-linéarité. Bien que cette relation plus complexe soit rarement utilisée dans les montres de tous les jours, elle souligne la sophistication potentielle de la mécanique élastique.
Conclusion du chapitre :
Voilà pour le ressort moteur, le point de départ de toute cette belle mécanique. Ce composant qui paraît simple joue pourtant un rôle critique en convertissant de l’énergie potentielle élastique en un couple prêt à être transféré aux autres composants. La tension monte, et notre aventure dans la mécanique horlogère ne fait que commencer.
Les Engrenages, ou l’art du partage de travail (et des petites rouages qui font le sale boulot)
Après avoir exploré le ressort moteur, passons maintenant à la machinerie complexe qui fait avancer tout le système : les engrenages. C’est ici que l’art du transfert de force prend vraiment tout son sens. Imaginez une chaîne de commandement où chaque rouage délègue soigneusement la tâche suivante, comme si chaque roue essayait d’éviter de faire tout le travail elle-même. Une vraie équipe de procrastinateurs bien organisée !
La relation entre les roues et les pignons
Un système de rouages est constitué de roues dentées et de pignons, chaque roue étant associée à un pignon, formant une liaison essentielle. Pour simplifier, on peut se concentrer sur une paire roue-pignon et définir la relation de transmission. Mathématiquement, le rapport des couples et des rayons s’écrit :
![]()
Ici :
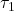 et
et 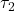 sont les couples respectifs exercés par les roues (en N.m).
sont les couples respectifs exercés par les roues (en N.m).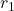 et
et 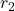 sont les rayons des roues correspondantes.
sont les rayons des roues correspondantes.
Ce rapport détermine comment la force est transmise entre les roues, permettant de contrôler le couple dans différentes parties du mécanisme. Si l’on souhaite augmenter le couple en aval, il suffit de faire tourner une roue plus petite reliée à une roue plus grande.
La vitesse angulaire et le ratio de transmission
En plus de transmettre la force, les engrenages permettent de modifier les vitesses angulaires. La relation entre les vitesses angulaires ![]() et
et ![]() des deux roues est donnée par :
des deux roues est donnée par :
![]()
Cela signifie qu’une roue plus grande fera tourner une roue plus petite plus rapidement, et inversement. Cette capacité de changer la vitesse de rotation est cruciale pour ajuster la vitesse de rotation des aiguilles de la montre.
Pour illustrer, si on choisit un ratio de 1:60, cela permet de convertir la rotation du ressort moteur (environ un tour par heure) en un mouvement plus lent et régulier pour les aiguilles.
Conservation de l’énergie dans le système de rouages
La conservation de l’énergie est une idée clé pour comprendre comment les roues interagissent entre elles. Lorsqu’on passe d’une roue à une autre, on conserve la puissance, définie comme le produit du couple et de la vitesse angulaire :
![]()
En supposant qu’il n’y ait pas de pertes (on va dire que nos rouages sont parfaits pour simplifier la discussion), la puissance transférée entre deux roues se conserve. Ainsi, pour une paire de roues interconnectées, on a :
![]()
Ce principe de conservation de la puissance nous aide à comprendre comment la force du ressort est répercutée tout au long du système de rouages sans perte significative de performance.
Les multiples niveaux de démultiplication
Dans une montre, le système de rouages est plus complexe qu’une simple paire de roues. Il comporte plusieurs niveaux d’engrenages qui permettent de gérer les variations de couple et de vitesse. Chaque étage d’engrenages doit être optimisé pour transférer l’énergie avec une efficacité maximale tout en minimisant les pertes dues aux frottements.
Par exemple, la transition de la roue des minutes à celle des heures implique généralement une démultiplication de 1:12, ce qui permet de ralentir progressivement le mouvement pour obtenir des aiguilles tournant à des vitesses différentes.
Les Engrenages : Les champions du relais (et de la procrastination organisée)
Les engrenages dans une montre sont un exemple parfait de collaboration mécanique bien huilée (littéralement). Chaque roue et chaque pignon contribuent à diviser la charge de travail tout en ajustant les vitesses et les couples, comme une équipe bien rodée qui se relaie pour faire avancer les choses. Cette section nous montre que même les machines doivent savoir déléguer !
Les Engrenages, ou l’art du partage de travail (et des petites rouages qui font le sale boulot)
Après avoir exploré le ressort moteur, passons maintenant à la machinerie complexe qui fait avancer tout le système : les engrenages. C’est ici que l’art du transfert de force prend vraiment tout son sens. Imaginez une chaîne de commandement où chaque rouage délègue soigneusement la tâche suivante, comme si chaque roue essayait d’éviter de faire tout le travail elle-même. Une vraie équipe de procrastinateurs bien organisée !
La relation entre les roues et les pignons
Un système de rouages est constitué de roues dentées et de pignons, chaque roue étant associée à un pignon, formant une liaison essentielle. Pour simplifier, on peut se concentrer sur une paire roue-pignon et définir la relation de transmission. Mathématiquement, le rapport des couples et des rayons s’écrit : ![]() Ici :
Ici :
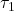 et
et 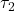 sont les couples respectifs exercés par les roues (en N.m).
sont les couples respectifs exercés par les roues (en N.m).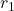 et
et 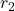 sont les rayons des roues correspondantes.
sont les rayons des roues correspondantes.
Ce rapport détermine comment la force est transmise entre les roues, permettant de contrôler le couple dans différentes parties du mécanisme. Si l’on souhaite augmenter le couple en aval, il suffit de faire tourner une roue plus petite reliée à une roue plus grande.
La vitesse angulaire et le ratio de transmission
En plus de transmettre la force, les engrenages permettent de modifier les vitesses angulaires. La relation entre les vitesses angulaires ![]() et
et ![]() des deux roues est donnée par :
des deux roues est donnée par : ![]() Cela signifie qu’une roue plus grande fera tourner une roue plus petite plus rapidement, et inversement. Cette capacité de changer la vitesse de rotation est cruciale pour ajuster la vitesse de rotation des aiguilles de la montre. Pour illustrer, si on choisit un ratio de 1:60, cela permet de convertir la rotation du ressort moteur (environ un tour par heure) en un mouvement plus lent et régulier pour les aiguilles.
Cela signifie qu’une roue plus grande fera tourner une roue plus petite plus rapidement, et inversement. Cette capacité de changer la vitesse de rotation est cruciale pour ajuster la vitesse de rotation des aiguilles de la montre. Pour illustrer, si on choisit un ratio de 1:60, cela permet de convertir la rotation du ressort moteur (environ un tour par heure) en un mouvement plus lent et régulier pour les aiguilles.
Conservation de l’énergie dans le système de rouages
La conservation de l’énergie est une idée clé pour comprendre comment les roues interagissent entre elles. Lorsqu’on passe d’une roue à une autre, on conserve la puissance, définie comme le produit du couple et de la vitesse angulaire : ![]() En supposant qu’il n’y ait pas de pertes (on va dire que nos rouages sont parfaits pour simplifier la discussion), la puissance transférée entre deux roues se conserve. Ainsi, pour une paire de roues interconnectées, on a :
En supposant qu’il n’y ait pas de pertes (on va dire que nos rouages sont parfaits pour simplifier la discussion), la puissance transférée entre deux roues se conserve. Ainsi, pour une paire de roues interconnectées, on a : ![]() Ce principe de conservation de la puissance nous aide à comprendre comment la force du ressort est répercutée tout au long du système de rouages sans perte significative de performance.
Ce principe de conservation de la puissance nous aide à comprendre comment la force du ressort est répercutée tout au long du système de rouages sans perte significative de performance.
Les multiples niveaux de démultiplication
Dans une montre, le système de rouages est plus complexe qu’une simple paire de roues. Il comporte plusieurs niveaux d’engrenages qui permettent de gérer les variations de couple et de vitesse. Chaque étage d’engrenages doit être optimisé pour transférer l’énergie avec une efficacité maximale tout en minimisant les pertes dues aux frottements. Par exemple, la transition de la roue des minutes à celle des heures implique généralement une démultiplication de 1:12, ce qui permet de ralentir progressivement le mouvement pour obtenir des aiguilles tournant à des vitesses différentes.
Les Engrenages : Les champions du relais (et de la procrastination organisée)
Les engrenages dans une montre sont un exemple parfait de collaboration mécanique bien huilée (littéralement). Chaque roue et chaque pignon contribuent à diviser la charge de travail tout en ajustant les vitesses et les couples, comme une équipe bien rodée qui se relaie pour faire avancer les choses. Cette section nous montre que même les machines doivent savoir déléguer !
L’échappement, cet anarchiste qui casse le mouvement
Maintenant que les engrenages font tout le boulot de manière ordonnée, il est temps d’aborder la partie rebelle de notre montre : l’échappement. Ce composant est un peu le punk de l’horlogerie, car au lieu de laisser tout tourner tranquillement, il décide de bloquer, libérer, puis bloquer à nouveau, en distribuant l’énergie au compte-goutte comme un maître de cérémonie autoritaire. Voyons comment ce système ingénieux régule la libération de l’énergie et permet à tout le reste de rester dans le bon tempo
La fonction de l’échappement
L’échappement a une double fonction : il régule la libération de l’énergie emmagasinée dans le ressort et fournit des impulsions régulières au balancier pour le maintenir en oscillation. L’échappement agit donc comme un convertisseur de mouvement continu (celui des rouages) en un mouvement oscillatoire, tout en contrôlant la vitesse de cette conversion. Pour imaginer cela, on peut penser à un gardien de porte qui autorise les personnes à entrer une par une (les personnes étant l’énergie).
Structure de l’échappement
L’échappement se compose principalement de la roue d’échappement et de l’ancre. La roue d’échappement a une forme particulière avec des dents spécialement conçues, tandis que l’ancre agit comme une barrière qui permet périodiquement à la roue de tourner par petits à-coups. Lorsque l’ancre libère une dent de la roue, cette dernière transfère un petit coup d’énergie au balancier, compensant les pertes dues aux frottements et maintenant ainsi l’oscillation.
Le transfert d’énergie et le couple d’impulsion
À chaque interaction entre la roue d’échappement et l’ancre, une petite quantité d’énergie est transférée au balancier. L’énergie transmise par impulsion est liée au couple appliqué par la roue d’échappement sur l’ancre. Si l’on considère que le couple exercé par la roue d’échappement est ![]() , l’énergie transférée à chaque impulsion est donnée par la relation suivante :
, l’énergie transférée à chaque impulsion est donnée par la relation suivante :![]()
où ![]() représente l’angle d’oscillation du balancier sur une impulsion. Ce transfert d’énergie régulier est essentiel pour maintenir l’oscillation du balancier et assurer la précision du système.
représente l’angle d’oscillation du balancier sur une impulsion. Ce transfert d’énergie régulier est essentiel pour maintenir l’oscillation du balancier et assurer la précision du système.
Modélisation de l’échappement comme oscillateur forcé
Pour bien comprendre ce qui se passe, on peut modéliser le balancier et l’échappement comme un système d’oscillateur forcé, où l’échappement fournit périodiquement une impulsion pour compenser les pertes d’énergie du balancier. Mathématiquement, l’équation du mouvement du balancier s’écrit comme un oscillateur harmonique forcé :![]()
où :
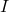 est le moment d’inertie du balancier.
est le moment d’inertie du balancier.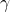 est le coefficient d’amortissement qui représente les pertes dues au frottement.
est le coefficient d’amortissement qui représente les pertes dues au frottement.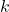 est la constante de torsion du ressort spiral, similaire à celle vue précédemment.
est la constante de torsion du ressort spiral, similaire à celle vue précédemment.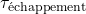 est le couple fourni par la roue d’échappement.
est le couple fourni par la roue d’échappement.
L’échappement agit donc comme une force extérieure périodique qui synchronise l’oscillation du balancier avec les impulsions qu’il reçoit.
La fréquence et la régularité du système
La régularité de l’échappement et du balancier est cruciale pour la précision de la montre. La fréquence naturelle de l’oscillateur est donnée par :![]()
et la période d’oscillation par :![]()
L’échappement est conçu pour délivrer des impulsions à une fréquence égale à celle du balancier, assurant ainsi un mouvement régulier des aiguilles. Toute dérive dans cette synchronisation entraînerait une perte de précision.
L’échappement : Le rebelle qui garde le contrôle (tout en cassant le rythme)
L’échappement est la pièce centrale qui perturbe volontairement le mouvement pour mieux le réguler. C’est une mécanique délicate, où chaque impulsion synchronise le système, un peu comme un batteur de jazz improvisant tout en maintenant le tempo. Ce mélange de chaos et de contrôle est ce qui fait de l’échappement une merveille de précision horlogère.
Le Balancier, l’athlète (pas si) paresseux qui assure la régularité
Nous avons vu comment l’échappement fournit des impulsions régulières au balancier, mais explorons maintenant de plus près ce fameux balancier. Si l’échappement est le batteur de jazz, le balancier est le métronome de la montre. Imaginez un athlète oscillant sans fin, essayant de maintenir son rythme parfait tout en compensant les petites imperfections du système. C’est ce balancier qui garantit la régularité du mouvement.
Le balancier-spiral comme oscillateur harmonique
Le balancier et son ressort spiral constituent un système oscillant qui peut être modélisé comme un oscillateur harmonique simple. La force de rappel fournie par le ressort spiral est proportionnelle à l’angle de déformation du balancier ![]() , ce qui nous mène à l’équation classique d’un oscillateur harmonique :
, ce qui nous mène à l’équation classique d’un oscillateur harmonique :![]()
où :
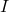 est le moment d’inertie du balancier, dépendant de sa masse et de sa forme.
est le moment d’inertie du balancier, dépendant de sa masse et de sa forme.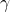 représente les pertes dues au frottement dans le pivot.
représente les pertes dues au frottement dans le pivot.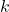 est la constante de torsion du ressort spiral.
est la constante de torsion du ressort spiral.
La fréquence naturelle du balancier
En l’absence de frottements significatifs (![]() ), la fréquence naturelle du balancier est donnée par :
), la fréquence naturelle du balancier est donnée par :![]()
Cette fréquence est cruciale, car elle détermine le rythme auquel les aiguilles avancent. La précision de la montre dépend de la capacité du balancier à maintenir cette fréquence malgré les perturbations externes et les variations de couple provenant de l’échappement.
Influence des facteurs environnementaux sur le balancier
Le balancier n’est malheureusement pas isolé du monde extérieur. Des facteurs tels que les variations de température, la gravité, et même les chocs affectent l’oscillation. Par exemple, une augmentation de la température provoque une dilatation du ressort spiral, diminuant ainsi la constante de torsion ![]() et, par conséquent, la fréquence
et, par conséquent, la fréquence ![]() . Pour corriger cela, les horlogers utilisent des matériaux à faible coefficient de dilatation thermique ou des spiraux compensateurs.
. Pour corriger cela, les horlogers utilisent des matériaux à faible coefficient de dilatation thermique ou des spiraux compensateurs.
L’isochronisme et le réglage fin
Une propriété clé que les horlogers cherchent à atteindre est l’isochronisme, c’est-à-dire l’indépendance de la période ![]() par rapport à l’amplitude de l’oscillation. En d’autres termes, quelle que soit la force appliquée au balancier, sa période doit rester constante. Pour approcher cet idéal, la géométrie du ressort spiral est optimisée et des ajustements sont faits au niveau du balancier pour minimiser les erreurs. L’isochronisme est mathématiquement défini par la relation suivante :
par rapport à l’amplitude de l’oscillation. En d’autres termes, quelle que soit la force appliquée au balancier, sa période doit rester constante. Pour approcher cet idéal, la géométrie du ressort spiral est optimisée et des ajustements sont faits au niveau du balancier pour minimiser les erreurs. L’isochronisme est mathématiquement défini par la relation suivante :![]()
ce qui signifie que les variations de l’amplitude ![]() n’ont qu’un effet négligeable sur la période
n’ont qu’un effet négligeable sur la période ![]() .
.
Le Balancier : Un métronome implacable (qui garde son calme même sous pression)
Le balancier est l’athlète silencieux qui assure la régularité de la montre. Bien que sensible aux perturbations, il est conçu pour les compenser et maintenir une oscillation aussi régulière qu’un métronome. À travers des siècles de perfectionnement, les horlogers ont fait du balancier une pièce aussi robuste que précise, le gardien imperturbable du temps.
Les Aiguilles, ou comment finir en beauté sans perdre la main
Après toutes ces étapes de transmission et de régulation de la force, il est temps d’aborder la partie visible de l’iceberg horloger : les aiguilles. Ces dernières sont comme les vedettes d’un spectacle parfaitement orchestré. Mais en coulisse, tout le travail se fait pour faire tourner ces aiguilles à des vitesses spécifiques et leur faire afficher l’heure avec une précision impitoyable.
Le rôle des aiguilles dans le système
Les aiguilles servent à indiquer l’heure grâce à leur mouvement autour du cadran. Mais attention, elles ne sont pas simplement posées sur un axe rotatif sans arrière-pensée ! Chaque aiguille doit être reliée à un système de rouages spécifique pour tourner à une vitesse définie par le rapport de démultiplication des engrenages. Par exemple, l’aiguille des minutes effectue un tour complet en 60 minutes, tandis que l’aiguille des heures réalise un tour en 12 heures.
Les rapports de transmission des aiguilles
Les aiguilles des minutes et des heures sont fixées sur des roues de tailles différentes. Mathématiquement, le rapport de transmission entre la roue des minutes et celle des heures est donné par :![]()
où :
 et
et  représentent les vitesses angulaires des roues des heures et des minutes respectivement.
représentent les vitesses angulaires des roues des heures et des minutes respectivement.
Conversion des rotations et réduction des erreurs
La transition entre les différentes roues et pignons est calculée de manière à minimiser les erreurs de synchronisation, tout en garantissant que chaque aiguille effectue son mouvement de manière fluide. Ce niveau de précision est atteint grâce à une conception minutieuse des engrenages et des axes, en tenant compte des tolérances mécaniques. L’ajustement minutieux des rapports de transmission permet également de réduire l’effet cumulé des petites erreurs.
L’énergie et l’inertie des aiguilles
Il est important de noter que les aiguilles, bien qu’elles soient relativement légères, possèdent une certaine inertie. Cette inertie peut provoquer des oscillations indésirables lorsque la montre subit des chocs ou des vibrations. La force de friction et la résistance à l’air jouent également un rôle dans le contrôle du mouvement des aiguilles. D’un point de vue énergétique, la puissance nécessaire pour faire tourner les aiguilles doit être suffisamment faible pour ne pas épuiser le système de rouages.
Les Aiguilles : Les stars qui volent la vedette (mais qui doivent tout à leur équipe)
Les aiguilles sont l’incarnation visible de tout le travail de précision accompli par les autres composants. Bien que leur tâche semble simple, elles sont les ambassadrices d’une mécanique complexe et délicate. Grâce à un calcul minutieux des rapports de transmission et à une gestion de l’inertie, les aiguilles parviennent à réaliser leur mission avec élégance et fiabilité.
La Dissipation d’Énergie, ou comment ne pas finir en PLS comme une mauvaise batterie de smartphone
Nous avons vu comment l’énergie est transmise et régulée à travers chaque étape du mécanisme d’une montre. Cependant, la dissipation d’énergie est l’ennemi silencieux de cette symphonie mécanique. Imaginez une montre comme un athlète qui doit gérer son énergie pour tenir la distance sans s’effondrer avant la ligne d’arrivée. Trop de pertes, et la montre ralentit ou s’arrête complètement. Plongeons dans les sources de dissipation d’énergie et les techniques utilisées pour les minimiser.
Les pertes par frottement dans les pivots
Chaque axe de rotation est supporté par des pivots, et chaque pivot subit des forces de frottement dues au contact avec les surfaces environnantes. Ce frottement, modélisé par la loi de Coulomb, est une source de perte d’énergie. La force de frottement ![]() est proportionnelle à la force normale
est proportionnelle à la force normale ![]() et au coefficient de frottement
et au coefficient de frottement ![]() :
:![]()
Pour minimiser ces pertes, des pierres précieuses comme le rubis sont utilisées dans les montres, réduisant ainsi le frottement et augmentant la durabilité des pivots.
La dissipation dans le ressort spiral
Le ressort spiral, en plus de fournir une force de rappel, subit également une certaine dissipation d’énergie par frottement interne. Les frottements moléculaires et les déformations internes du matériau contribuent à cette dissipation. Cette perte d’énergie peut être modélisée en ajoutant un terme d’amortissement dans l’équation du mouvement du balancier :![]()
où ![]() représente les pertes d’énergie internes au ressort spiral.
représente les pertes d’énergie internes au ressort spiral.
Les pertes dues aux chocs et vibrations externes
Les montres sont exposées à des perturbations externes telles que des chocs et des vibrations. Ces perturbations introduisent des mouvements supplémentaires dans les composants, augmentant la dissipation d’énergie par des frottements parasites et des déformations élastiques. Les horlogers utilisent des systèmes antichocs comme l’Incabloc pour amortir ces vibrations et réduire les pertes d’énergie.
La gestion des pertes thermiques
En plus des pertes par frottement mécanique, les montres subissent des variations thermiques qui affectent les propriétés des matériaux. Par exemple, une élévation de température peut provoquer une dilatation des composants métalliques, augmentant le frottement et les pertes énergétiques. Les montres haut de gamme utilisent des matériaux spéciaux, tels que les alliages invar, pour minimiser les effets des variations de température.
La Dissipation d’Énergie : L’art de rester efficace (et d’éviter la panne sèche)
La dissipation d’énergie est une réalité inévitable, mais elle peut être maîtrisée avec des choix intelligents de matériaux et de conception. En réduisant les pertes par frottement et en optimisant la résistance aux perturbations externes, les horlogers parviennent à maximiser l’efficacité énergétique et la précision des montres. Après tout, même un athlète bien entraîné doit savoir gérer son énergie pour rester performant jusqu’à la fin.
Conclusion : « Une montre, une machine à voyager dans le temps (ou presque) »
Après ce voyage à travers les rouages, ressorts, et échappements, il est clair que chaque composant d’une montre mécanique joue un rôle essentiel dans cette symphonie complexe. Du ressort moteur qui stocke l’énergie comme un étudiant sous pression, aux engrenages qui se la refilent en faisant mine de ne pas tout porter sur leurs épaules, jusqu’à l’échappement qui casse le rythme pour mieux le contrôler, chaque élément contribue à transformer une tension initiale en un ballet précis des aiguilles.
À travers notre analyse, nous avons découvert que ce qui semble être un simple « tic-tac » est en réalité un chef-d’œuvre de physique appliquée et d’ingénierie mécanique. Les lois fondamentales de la mécanique classique, l’élasticité, la régulation des oscillateurs et la gestion des pertes se rencontrent ici dans un espace réduit à la taille d’une poche.
Une montre mécanique est bien plus qu’un bijou fonctionnel ; c’est une petite leçon de physique embarquée, un rappel que même les objets les plus quotidiens peuvent receler une complexité mathématique et technique incroyable. C’est comme porter une version miniature d’un cours avancé de mécanique sur votre poignet, sans même avoir à réviser.
En fin de compte, comprendre le mécanisme de transfert de force dans une montre, c’est comme plonger dans une version microcosmique de l’univers : tout fonctionne grâce à l’énergie, aux interactions de forces, et à l’éternelle lutte contre la dissipation. Et si jamais vous vous perdez dans le temps, vous saurez au moins qu’il y a tout un orchestre mécanique jouant pour vous ramener à l’heure.
 Pourton.info
Pourton.info 



