Chapitre 1 : Introduction : Pourquoi les Bosons Ont-ils Toujours la Meilleure Part?
Les bosons, ces petites particules obéissant aux lois de la mécanique quantique, semblent toujours avoir la part belle dans l’univers quantique. Mais pourquoi donc ? Pour bien comprendre, il faut remonter à la découverte de ces charmants fêtards de la physique.
Les bosons tirent leur nom de Satyendra Nath Bose, un physicien indien qui, en 1924, envoya un article révolutionnaire à Albert Einstein. Cet article portait sur les statistiques de photons, ces particules de lumière. Einstein, impressionné, traduisit et publia l’article, posant ainsi les bases des statistiques de Bose-Einstein. À partir de là, le monde des particules n’allait plus jamais être le même.
Alors, qu’est-ce qui différencie les bosons des fermions, leurs cousins obéissant au principe d’exclusion de Pauli ? Les fermions, nommés d’après Enrico Fermi, ne peuvent pas partager le même état quantique. Imaginez une fête où chaque invité doit avoir son propre siège. Les bosons, en revanche, sont les rois de la fête. Ils peuvent se tasser dans le même état quantique sans problème, transformant la piste de danse quantique en une véritable rave party.

Les exemples les plus célèbres de bosons incluent les photons (particules de lumière), les gluons (qui collent les quarks ensemble dans les protons et les neutrons), et les particules alpha. Grâce à leur nature conviviale, les bosons sont responsables de certains des phénomènes les plus fascinants en physique, comme la condensation de Bose-Einstein, où un grand nombre de bosons se regroupent dans le même état quantique à des températures extrêmement basses.
Mais pour vraiment comprendre pourquoi les bosons sont les stars de la physique quantique, il faut plonger dans les mathématiques qui régissent leur comportement. Et c’est exactement ce que nous allons faire dans les chapitres suivants.
Restez avec nous, car nous allons découvrir comment les bosons transforment la physique en une fête permanente, avec des intégrales, des fonctions de partition et des distributions de probabilité qui vous donneront envie de danser (ou de résoudre des équations, c’est selon).
Chapitre 2 : Fonction de Partition : Le Saint Graal des Bosons

Pour comprendre comment les bosons se comportent dans un système, il est essentiel de plonger dans la fonction de partition. C’est un peu comme trouver la recette secrète de la potion magique qui décrit tout ce que nous devons savoir sur un système quantique. Alors, sortons nos grimoires de mathématiques et voyons de quoi il en retourne.
La fonction de partition pour un système de bosons est définie comme suit :
![]()
où :
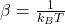 (l’inverse de la température multipliée par la constante de Boltzmann),
(l’inverse de la température multipliée par la constante de Boltzmann),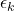 est l’énergie de l’état
est l’énergie de l’état 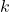 ,
,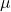 est le potentiel chimique.
est le potentiel chimique.
Cette fonction de partition, notée ![]() , est une sorte de super calculateur statistique. Elle nous permet de déterminer les propriétés thermodynamiques du système de bosons. En fait, toute la physique statistique du système peut être déduite à partir de cette fonction.
, est une sorte de super calculateur statistique. Elle nous permet de déterminer les propriétés thermodynamiques du système de bosons. En fait, toute la physique statistique du système peut être déduite à partir de cette fonction.
Alors, pourquoi est-ce le Saint Graal ? Parce que la fonction de partition encapsule toutes les informations nécessaires pour décrire un système en équilibre thermodynamique. C’est un peu comme si vous aviez toutes les recettes de cuisine dans un seul livre. Vous pouvez cuisiner n’importe quel plat en vous référant simplement aux pages appropriées.
Pour mieux comprendre, prenons un état d’énergie particulier ![]() . La fonction de partition pour cet état est :
. La fonction de partition pour cet état est :
![]()
Cette série géométrique converge pour ![]() , et nous pouvons la simplifier en :
, et nous pouvons la simplifier en :
![]()
En d’autres termes, la fonction de partition pour un état donné nous donne la probabilité que cet état soit occupé par un certain nombre de bosons. Mais attention, ne nous arrêtons pas là, car la vraie magie réside dans la combinaison de toutes ces fonctions de partition individuelles pour obtenir une description complète du système.
Lorsque nous combinons toutes les fonctions de partition individuelles, nous obtenons la fonction de partition totale pour le système :
![]()
Cette équation peut sembler intimidante, mais elle est en réalité une boîte à outils extrêmement puissante pour les physiciens. Avec ![]() en main, nous pouvons dériver d’autres propriétés thermodynamiques cruciales, telles que l’énergie libre, l’entropie et bien d’autres.
en main, nous pouvons dériver d’autres propriétés thermodynamiques cruciales, telles que l’énergie libre, l’entropie et bien d’autres.
Alors, prenez vos calculateurs et vos crayons, car la fête ne fait que commencer. Dans le prochain chapitre, nous découvrirons comment utiliser cette fonction de partition pour obtenir la distribution de Bose-Einstein, la clé pour comprendre le comportement des bosons.
Chapitre 3 : Distribution de Bose-Einstein : La Recette Secrète des Bosons

Maintenant que nous avons notre fonction de partition, il est temps de découvrir la distribution de Bose-Einstein, l’ingrédient secret qui décrit comment les bosons se répartissent entre les différents états d’énergie.
La distribution de Bose-Einstein donne le nombre moyen de bosons ![]() dans un état d’énergie
dans un état d’énergie ![]() :
:
![]()
Décomposons cette équation pour en comprendre la signification.
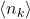 est le nombre moyen de particules dans l’état
est le nombre moyen de particules dans l’état 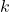 .
.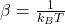 , où
, où 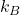 est la constante de Boltzmann et
est la constante de Boltzmann et 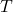 la température.
la température.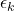 est l’énergie de l’état
est l’énergie de l’état 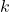 .
.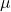 est le potentiel chimique, qui ajuste le nombre total de particules dans le système.
est le potentiel chimique, qui ajuste le nombre total de particules dans le système.
Pour dériver cette distribution, nous partons de la fonction de partition grand-canonique pour un seul état d’énergie ![]() :
:
![]()
Cette série géométrique se résout en :
![]()
Ensuite, nous utilisons cette fonction de partition pour trouver la probabilité ![]() que l’état
que l’état ![]() soit occupé par
soit occupé par ![]() bosons :
bosons :
![]()
Le nombre moyen de particules dans cet état est alors donné par :
![]()
En utilisant la formule de ![]() , nous obtenons :
, nous obtenons :
![]()
En substituant ![]() , nous trouvons :
, nous trouvons :
![]()
Cette dérivation nous ramène à la distribution de Bose-Einstein :
![]()
Et voilà ! Nous avons maintenant notre recette secrète pour déterminer comment les bosons se répartissent entre les différents états d’énergie.
Mais pourquoi cette distribution est-elle si spéciale ? Parce qu’elle explique pourquoi les bosons aiment se regrouper. À des températures très basses, un grand nombre de bosons peut occuper le même état d’énergie, donnant lieu à des phénomènes fascinants comme la condensation de Bose-Einstein. En d’autres termes, les bosons sont des créatures sociales qui adorent se rassembler, contrairement aux fermions qui préfèrent garder leurs distances.
Alors, préparez-vous, car dans le prochain chapitre, nous allons explorer la densité d’états et découvrir combien de bosons peuvent réellement danser sur la tête d’une épingle.
Chapitre 4 : Densité d’États : Combien de Bosons Dansent sur la Tête d’une Épingle?

Maintenant que nous avons notre distribution de Bose-Einstein, il est temps de voir comment cette distribution se combine avec la densité d’états pour nous donner une image complète du comportement des bosons dans un système. La densité d’états nous indique combien d’états d’énergie sont disponibles dans une certaine gamme d’énergie.
Pour un système de particules en trois dimensions, la densité d’états ![]() est donnée par :
est donnée par :
![]()
où :
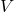 est le volume du système,
est le volume du système,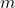 est la masse des particules,
est la masse des particules,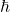 est la constante de Planck réduite,
est la constante de Planck réduite, est l’énergie.
est l’énergie.
La densité d’états nous dit combien d’états d’énergie sont disponibles par unité de volume et par unité d’énergie. Plus l’énergie est élevée, plus il y a d’états disponibles pour les bosons.
Intégration de la Densité d’États et de la Distribution de Bose-Einstein
Pour obtenir le nombre total de bosons dans le système, nous devons intégrer la distribution de Bose-Einstein sur toutes les énergies possibles, en tenant compte de la densité d’états. Le nombre total de particules ![]() est donné par :
est donné par :
![]()
En substituant ![]() , nous avons :
, nous avons :
![]()
Cette intégrale peut sembler intimidante, mais elle est essentielle pour comprendre le comportement global des bosons dans un système. Elle nous permet de déterminer combien de bosons sont présents à différentes énergies et comment ils se répartissent dans le système.
L’Énergie Totale du Système
De la même manière, nous pouvons calculer l’énergie totale ![]() du système en intégrant la densité d’états pondérée par l’énergie et la distribution de Bose-Einstein :
du système en intégrant la densité d’états pondérée par l’énergie et la distribution de Bose-Einstein :
![]()
En substituant ![]() , nous avons :
, nous avons :
![]()
Ces intégrales sont essentielles pour la thermodynamique des gaz de bosons. Elles nous permettent de calculer des propriétés thermodynamiques comme l’énergie interne, l’entropie, et la capacité thermique du système.
Condensation de Bose-Einstein
Un phénomène particulièrement fascinant qui émerge de ces intégrales est la condensation de Bose-Einstein. À des températures suffisamment basses, un nombre macroscopique de bosons peut occuper l’état fondamental, conduisant à une phase de la matière totalement nouvelle. Cette phase, prédite par Einstein en 1925, a été observée expérimentalement pour la première fois en 1995 avec des atomes de rubidium refroidis par laser.
En d’autres termes, quand la température baisse suffisamment, tous les bosons décident de faire la fête dans le même état quantique, créant un superfluide ou un supraconducteur avec des propriétés étonnantes.
Alors, préparez-vous pour le prochain chapitre où nous explorerons en détail le phénomène de la condensation de Bose-Einstein et découvrirons pourquoi les bosons adorent se regrouper quand il fait très froid.
Chapitre 5 : Condensation de Bose-Einstein : Quand les Bosons Font la Fête au Zéro Absolu

La condensation de Bose-Einstein (CBE) est l’un des phénomènes les plus fascinants en physique des particules. Imaginez un groupe de bosons décidant de faire la fête dans le même état quantique à des températures proches du zéro absolu. C’est exactement ce qui se passe lors de la condensation de Bose-Einstein.
Théorie de la Condensation de Bose-Einstein
Pour comprendre ce phénomène, nous devons d’abord considérer la fonction de partition et la distribution de Bose-Einstein que nous avons déjà explorées. À des températures très basses, le potentiel chimique ![]() approche de la plus basse énergie possible de l’état fondamental, ce qui entraîne une occupation macroscopique de cet état.
approche de la plus basse énergie possible de l’état fondamental, ce qui entraîne une occupation macroscopique de cet état.
Pour un gaz de bosons, la transition vers la CBE se produit lorsque la densité de particules dépasse une valeur critique à une température critique ![]() . La température critique est donnée par :
. La température critique est donnée par :
![]()
où :
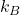 est la constante de Boltzmann,
est la constante de Boltzmann,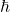 est la constante de Planck réduite,
est la constante de Planck réduite,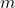 est la masse du boson,
est la masse du boson,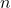 est la densité de particules,
est la densité de particules,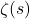 est la fonction zêta de Riemann.
est la fonction zêta de Riemann.
Distribution à Températures Inférieures à 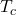
À des températures inférieures à ![]() , une fraction significative de bosons occupe l’état fondamental
, une fraction significative de bosons occupe l’état fondamental ![]() . Le nombre de particules dans l’état fondamental est donné par :
. Le nombre de particules dans l’état fondamental est donné par :
![]()
où ![]() est le nombre total de particules. Cette relation montre qu’à
est le nombre total de particules. Cette relation montre qu’à ![]() , toutes les particules se trouvent dans l’état fondamental.
, toutes les particules se trouvent dans l’état fondamental.
Applications et Expériences
La condensation de Bose-Einstein a été observée pour la première fois en 1995 par Eric Cornell et Carl Wieman, utilisant des atomes de rubidium refroidis par laser. Cette découverte leur a valu le prix Nobel de physique en 2001. Depuis, la CBE a été observée dans divers systèmes, ouvrant la voie à de nombreuses applications en physique et en technologie.
Superfluidité et Supraconductivité
La CBE est à la base de phénomènes tels que la superfluidité et la supraconductivité. Dans un superfluide, comme l’hélium-4 à des températures proches du zéro absolu, les atomes se déplacent sans viscosité, ce qui permet des écoulements sans friction. De même, la supraconductivité, observée dans certains matériaux à basse température, permet la conduction électrique sans résistance.
Lasers à Atomes et Interférométrie Quantique
Les condensats de Bose-Einstein sont également utilisés pour créer des lasers à atomes, où des faisceaux cohérents d’atomes peuvent être manipulés avec une précision extrême. Ces lasers ouvrent de nouvelles possibilités en interférométrie quantique, permettant des mesures ultra-précises de la gravité, du temps et des champs magnétiques.
On en déduit que …
La condensation de Bose-Einstein illustre magnifiquement comment la physique quantique peut donner naissance à des phénomènes macroscopiques extraordinaires. À des températures proches du zéro absolu, les bosons révèlent leur nature sociale, s’assemblant en une seule entité quantique avec des propriétés uniques et fascinantes.
Restez avec nous, car dans le prochain chapitre, nous explorerons comment intégrer toutes ces connaissances pour comprendre les propriétés thermodynamiques des gaz de bosons. Nous plongerons dans les intégrales thermodynamiques et découvrirons comment ces concepts mathématiques élégants décrivent le comportement des bosons à différentes échelles de température.
Chapitre 6 : Intégrales Thermodynamiques : Intégration ou Intoxication?

Les intégrales thermodynamiques sont les outils mathématiques essentiels pour comprendre le comportement global des gaz de bosons. Elles nous permettent de relier les propriétés microscopiques des particules à leurs propriétés macroscopiques, comme l’énergie, l’entropie et la capacité thermique. Alors, plongeons dans ces intégrales et voyons comment elles décrivent notre système de bosons.
Nombre Total de Particules
Nous avons déjà vu que le nombre total de particules ![]() est donné par l’intégrale :
est donné par l’intégrale :
![]()
En utilisant la densité d’états ![]() pour un système de particules non relativistes en 3 dimensions, nous avons :
pour un système de particules non relativistes en 3 dimensions, nous avons :
![]()
Ainsi, l’intégrale devient :
![]()
Cette intégrale peut être résolue en utilisant la substitution ![]() , ce qui donne :
, ce qui donne :
![]()
Pour des températures suffisamment élevées (où ![]() ), cette intégrale est bien connue et peut être exprimée en termes de la fonction zêta de Riemann
), cette intégrale est bien connue et peut être exprimée en termes de la fonction zêta de Riemann ![]() :
:
![]()
où ![]() est la fonction gamma d’Euler. Ainsi, nous avons :
est la fonction gamma d’Euler. Ainsi, nous avons :
![]()
Énergie Totale
De la même manière, l’énergie totale ![]() du système est donnée par :
du système est donnée par :
![]()
En utilisant la densité d’états, cela devient :
![]()
En effectuant la même substitution ![]() , nous obtenons :
, nous obtenons :
![]()
Pour des températures élevées, cette intégrale peut également être exprimée en termes de la fonction zêta de Riemann :
![]()
Capacité Thermique
La capacité thermique à volume constant ![]() est donnée par la dérivée de l’énergie par rapport à la température :
est donnée par la dérivée de l’énergie par rapport à la température :
![]()
En utilisant notre expression pour ![]() , nous avons :
, nous avons :
![]()
où ![]() est une constante dépendant des paramètres du système. Donc :
est une constante dépendant des paramètres du système. Donc :
![]()
Ces résultats montrent comment les intégrales thermodynamiques permettent de relier les propriétés microscopiques des particules (comme leur masse et leur densité) aux propriétés macroscopiques du système (comme l’énergie et la capacité thermique).
En résumé
Les intégrales thermodynamiques sont les clés qui nous permettent de comprendre le comportement des gaz de bosons à différentes températures. En combinant la densité d’états avec la distribution de Bose-Einstein, nous pouvons calculer des propriétés thermodynamiques essentielles qui décrivent comment les bosons interagissent et se comportent à l’échelle macroscopique.
Préparez-vous pour le prochain chapitre où nous explorerons les applications modernes des bosons et découvrirons comment ces particules fascinantes sont utilisées dans la technologie d’aujourd’hui.
Chapitre 7 : Applications Modernes : Bosons et Technologie, une Histoire d’Amour Moderne

Les bosons, grâce à leurs propriétés uniques, ont trouvé des applications fascinantes dans la technologie moderne. De la supraconductivité aux lasers à atomes, leur capacité à occuper le même état quantique ouvre des possibilités incroyables pour la science et l’ingénierie. Plongeons dans quelques-unes de ces applications.
Supraconductivité : Conduction Sans Résistance
L’un des exemples les plus célèbres d’application des bosons est la supraconductivité. Les électrons, qui sont des fermions, peuvent former des paires de Cooper à basse température. Ces paires de Cooper se comportent comme des bosons et peuvent entrer en état de condensation de Bose-Einstein, permettant la conduction électrique sans résistance.
En supraconductivité, les paires de Cooper se déplacent sans rencontrer d’obstacles, ce qui signifie qu’il n’y a pas de dissipation d’énergie sous forme de chaleur. Cela permet de transporter des courants électriques avec une efficacité parfaite, ouvrant la voie à des applications telles que les aimants supraconducteurs utilisés dans les IRM et les lignes de transmission électrique sans pertes.
Superfluidité : Liquides Sans Viscosité
Un autre phénomène fascinant est la superfluidité, observée dans des liquides comme l’hélium-4 à des températures proches du zéro absolu. L’hélium-4, étant un boson, peut entrer en état de superfluidité, où il s’écoule sans viscosité.
En superfluidité, les atomes de l’hélium-4 se comportent comme un seul superfluide cohérent. Cela permet des phénomènes étranges comme l’écoulement sans friction à travers des canaux minuscules et la montée le long des parois de récipients. Ces propriétés sont utilisées dans des domaines allant de la cryogénie à la recherche fondamentale en physique des fluides.
Lasers à Atomes : Faisceaux Coherents d’Atomes
Les condensats de Bose-Einstein ont également été utilisés pour créer des lasers à atomes, où des faisceaux cohérents d’atomes sont produits et manipulés avec une précision extrême. Contrairement aux lasers optiques traditionnels qui utilisent des photons, les lasers à atomes utilisent des particules matérielles, offrant des possibilités uniques pour l’interférométrie quantique.
Les lasers à atomes sont utilisés pour des mesures ultra-précises de la gravité, du temps et des champs magnétiques. Par exemple, des gyroscopes quantiques basés sur des lasers à atomes permettent de naviguer avec une précision sans précédent, et des horloges atomiques améliorées repoussent les limites de la mesure du temps.
Interférométrie Quantique : Mesures Ultra-Précises
L’interférométrie quantique utilise les propriétés ondulatoires des bosons pour réaliser des mesures extrêmement précises. En utilisant des condensats de Bose-Einstein dans des dispositifs interférométriques, les scientifiques peuvent mesurer des variations infinitésimales de champs gravitationnels et magnétiques.
Ces techniques sont utilisées dans des applications telles que la détection des ondes gravitationnelles, la cartographie des anomalies gravitationnelles terrestres et la recherche sur la matière noire. L’interférométrie quantique offre des perspectives passionnantes pour comprendre les phénomènes les plus fondamentaux de l’univers.
Ordinateurs Quantiques : Bits Quantiques Bosoniques
Les bosons jouent également un rôle potentiel dans le développement des ordinateurs quantiques. Les bits quantiques (qubits) basés sur des bosons peuvent offrir des avantages en termes de manipulation et de cohérence par rapport aux qubits fermioniques. Par exemple, des qubits photoniques utilisent les propriétés des photons pour réaliser des calculs quantiques avec une grande rapidité et efficacité.
Il en résulte que …
Les applications modernes des bosons montrent à quel point ces particules jouent un rôle crucial dans la technologie et la recherche scientifique. Leur capacité unique à occuper le même état quantique ouvre des possibilités incroyables, des supraconducteurs aux lasers à atomes, en passant par l’interférométrie quantique et les ordinateurs quantiques.
Restez avec nous pour le dernier chapitre où nous résumerons les points clés et réfléchirons à l’avenir des bosons dans la science et la technologie.
Chapitre 8 : Conclusion : Les Bosons, Ces Fêtards Quantiques Incontournables

Les bosons, avec leur nature sociale et leurs propriétés uniques, ont transformé notre compréhension de l’univers quantique et ouvert de nouvelles avenues en technologie et en recherche scientifique. Revenons sur les points clés que nous avons explorés dans cet article et réfléchissons à ce que l’avenir pourrait réserver aux bosons.
Récapitulatif des Points Clés
- Introduction aux Bosons : Nous avons découvert comment les bosons, à l’opposé des fermions, peuvent partager le même état quantique, permettant des phénomènes fascinants comme la condensation de Bose-Einstein.
- Fonction de Partition : La fonction de partition est notre outil clé pour comprendre le comportement des bosons. Elle encapsule toutes les informations nécessaires pour décrire un système en équilibre thermodynamique.
- Distribution de Bose-Einstein : Nous avons dérivé la distribution de Bose-Einstein, qui décrit comment les bosons se répartissent entre les différents états d’énergie, révélant leur tendance à se regrouper à basse température.
- Densité d’États : La densité d’états nous indique combien d’états d’énergie sont disponibles pour les bosons dans un système, nous permettant de calculer des propriétés macroscopiques comme le nombre total de particules et l’énergie totale.
- Condensation de Bose-Einstein : À des températures proches du zéro absolu, les bosons peuvent entrer en état de condensation de Bose-Einstein, conduisant à des phénomènes tels que la superfluidité et la supraconductivité.
- Intégrales Thermodynamiques : Les intégrales thermodynamiques sont essentielles pour relier les propriétés microscopiques des particules aux propriétés macroscopiques du système, telles que l’énergie et la capacité thermique.
- Applications Modernes : Les bosons ont trouvé des applications fascinantes dans des domaines comme la supraconductivité, la superfluidité, les lasers à atomes, l’interférométrie quantique, et les ordinateurs quantiques.
Réflexions sur l’Avenir
L’avenir des bosons dans la science et la technologie semble prometteur. Avec les avancées continues en physique quantique et en technologie de manipulation des particules, nous pouvons nous attendre à des découvertes encore plus passionnantes et à des applications révolutionnaires.
Supraconducteurs à Haute Température
La recherche sur les supraconducteurs à haute température pourrait un jour conduire à des matériaux capables de conduire l’électricité sans résistance à des températures bien supérieures à celles actuellement nécessaires. Cela pourrait révolutionner des secteurs entiers, de la production et la distribution d’énergie à l’électronique.
Applications Médicales
Les avancées dans les technologies quantiques basées sur les bosons, comme les IRM supraconducteurs, continueront à améliorer les capacités de diagnostic médical, offrant des images plus précises et des traitements plus efficaces.
Exploration de l’Univers
L’interférométrie quantique et les autres techniques basées sur les bosons permettront des explorations plus profondes de l’univers, nous aidant à comprendre des phénomènes comme la matière noire, l’énergie noire, et les ondes gravitationnelles avec une précision sans précédent.
Conclusion Finale
Les bosons, avec leur penchant pour la fête quantique, ont ouvert de nouvelles perspectives pour la science et la technologie. Leur capacité unique à se regrouper et à entrer en état de condensation de Bose-Einstein continue de fasciner les chercheurs et d’inspirer des innovations technologiques.
Alors, que vous soyez un physicien passionné, un ingénieur innovant ou simplement quelqu’un curieux de comprendre les mystères de l’univers, souvenez-vous que les bosons seront toujours là, dansant ensemble sur la scène quantique, prêts à nous dévoiler les secrets les plus profonds de la nature.
 Pourton.info
Pourton.info 



