Introduction aux Problèmes Mathématiques Avancés
Les mathématiques avancées constituent un domaine fascinant, rempli de défis intellectuels et de concepts profonds qui trouvent des applications dans divers domaines tels que la physique, l’ingénierie, l’économie, et bien d’autres. Cet article explore quelques-uns de ces concepts, en se concentrant sur des techniques spécifiques telles que les limites impliquant des séries de Taylor, la dérivation implicite, les séries de Maclaurin, et bien plus encore.
Dans ce premier chapitre, nous poserons le cadre pour comprendre l’importance de ces techniques et leurs applications pratiques. Nous examinerons comment ces concepts se manifestent dans des problèmes concrets et leur utilité pour résoudre des équations complexes, optimiser des fonctions et analyser des courbes.
Importance des Concepts Abordés
Les techniques mathématiques avancées abordées dans cet article ne sont pas seulement des exercices académiques, mais des outils puissants utilisés dans de nombreux domaines. Par exemple, la série de Taylor est essentielle pour approcher des fonctions complexes et est largement utilisée dans la physique pour modéliser des phénomènes naturels. De même, la dérivation implicite est une méthode clé pour trouver les taux de changement dans des systèmes où les variables sont interdépendantes.
Aperçu des Techniques
- Limites et Séries de Taylor : Nous verrons comment développer des séries de Taylor pour résoudre des limites complexes, une technique cruciale en analyse mathématique.
- Dérivation Implicite : Une méthode pour traiter les fonctions où les variables ne sont pas explicitement définies, ce qui est fréquent dans de nombreux problèmes pratiques.
- Optimisation de Courbes : Techniques pour trouver les points critiques et optimiser les fonctions, avec des applications en économie et en ingénierie.
- Intégrales et Séries de Maclaurin : Utilisation des séries de Maclaurin pour représenter des intégrales comme des sommes de séries infinies, une technique utile en analyse et en calcul.
- Fonctions Multivariables et Contraintes : Méthodes pour analyser des fonctions avec plusieurs variables et contraintes, y compris les multiplicateurs de Lagrange.
Applications Pratiques
Les mathématiques avancées trouvent des applications dans de nombreux domaines. Par exemple, en physique, les séries de Taylor et de Maclaurin sont utilisées pour modéliser des systèmes physiques et approcher des solutions d’équations différentielles. En économie, l’optimisation des fonctions permet de maximiser les profits ou de minimiser les coûts. L’ingénierie utilise également ces techniques pour analyser et concevoir des systèmes complexes.
Anecdotes Historiques
Pour rendre cette exploration plus vivante, nous intégrerons des anecdotes historiques illustrant l’évolution des concepts mathématiques. Par exemple, nous discuterons de l’impact des travaux de Joseph Fourier sur les séries de Fourier, qui ont révolutionné l’analyse des ondes et des vibrations, et des contributions de nombreux autres mathématiciens qui ont façonné les techniques que nous utilisons aujourd’hui.
Ce premier chapitre a pour but de vous préparer à plonger dans des problèmes mathématiques complexes avec une compréhension claire de leur importance et de leurs applications pratiques. Dans les chapitres suivants, nous explorerons en détail chaque technique, en fournissant des exemples concrets et des explications approfondies.
Analyse de Limites Impliquant des Séries de Taylor
Les limites jouent un rôle central en analyse mathématique, et lorsqu’il s’agit de limites complexes, les séries de Taylor se révèlent être un outil puissant. Dans ce chapitre, nous explorerons comment utiliser les séries de Taylor pour résoudre des limites complexes, en illustrant cela par un exemple pratique.
Développement de Séries de Taylor
La série de Taylor d’une fonction ![]() autour d’un point
autour d’un point ![]() est donnée par :
est donnée par :
![]()
Cette série permet d’approximer des fonctions en termes de polynômes, facilitant ainsi le calcul des limites. Pour illustrer cette technique, considérons l’exemple suivant :
Exemple Pratique
Supposons que ![]() est différentiable en
est différentiable en ![]() . Évaluons la limite suivante en termes de
. Évaluons la limite suivante en termes de ![]() et
et ![]() :
:
![]()
Pour résoudre cette limite, nous utilisons les séries de Taylor et les approximations logarithmiques.
- Approximons
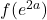 autour de
autour de 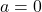 :
:
![]()
Donc,
![]()
- Approximons le logarithme :
![]()
Ainsi, la limite devient :
![]()
Pour simplifier ![]() , nous pouvons utiliser une approximation binomiale :
, nous pouvons utiliser une approximation binomiale :
![]()
La limite devient donc :
![]()
![]()
![]()
![]()
Importance des Séries de Taylor
Les séries de Taylor sont fondamentales pour l’analyse et les approximations en mathématiques. Elles permettent de simplifier des expressions complexes et sont utilisées dans divers domaines, tels que la physique pour modéliser des phénomènes naturels, et l’ingénierie pour analyser des systèmes dynamiques.
Applications Réelles
En physique, les séries de Taylor sont utilisées pour approximations lorsque les solutions exactes sont difficiles à obtenir. Par exemple, dans la mécanique quantique, elles sont employées pour résoudre des équations différentielles complexes. En ingénierie, elles servent à modéliser des systèmes et à prévoir leur comportement sous différentes conditions.
Anecdotes Historiques
L’utilisation des séries de Taylor remonte à Brook Taylor, un mathématicien anglais du début du XVIIIe siècle. Sa découverte a transformé l’analyse mathématique, permettant de nouvelles approches pour résoudre des problèmes complexes. Les séries de Taylor sont devenues un outil indispensable dans de nombreux domaines scientifiques et techniques.
Ce chapitre a montré comment les séries de Taylor peuvent être utilisées pour résoudre des limites complexes, illustrées par un exemple pratique. Dans le chapitre suivant, nous explorerons la dérivation implicite et ses applications.
Dérivation Implicite et Applications Pratiques
La dérivation implicite est une technique essentielle en analyse mathématique, particulièrement utile lorsque les variables sont interdépendantes et qu’il n’est pas possible d’exprimer une variable explicitement en fonction de l’autre. Dans ce chapitre, nous explorerons la méthodologie de la dérivation implicite et illustrerons son application avec un exemple concret.
Méthodologie de la Dérivation Implicite
La dérivation implicite consiste à différencier chaque terme d’une équation qui lie plusieurs variables, en tenant compte du fait que ces variables peuvent dépendre implicitement les unes des autres. Pour ce faire, nous utilisons la règle de la chaîne et nous appliquons les dérivées à chaque terme, tout en résolvant pour la dérivée recherchée.
Exemple Pratique
Considérons l’équation suivante :
![]()
Nous devons calculer ![]() au point
au point ![]() .
.
- Simplifions l’équation :
![]()
À ![]() , cette équation devient :
, cette équation devient :
![]()
- Différention implicite par rapport à
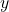 :
:
![]()
- Appliquons la règle de la chaîne :
![]()
Simplifions :
![]()
![]()
![]()
- Calculons
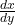 à
à 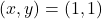 :
:
![]()
Applications Pratiques de la Dérivation Implicite
La dérivation implicite est utilisée dans de nombreux domaines pour analyser des systèmes où les variables sont interdépendantes. Par exemple, en physique, elle est employée pour résoudre des problèmes de dynamique où plusieurs variables sont liées par des équations complexes. En économie, la dérivation implicite permet d’analyser les taux de changement dans les modèles économiques où les variables sont interdépendantes.
Anecdotes Historiques
La dérivation implicite a été utilisée par de nombreux mathématiciens célèbres, notamment Isaac Newton et Gottfried Wilhelm Leibniz, lors du développement du calcul différentiel. Cette technique a permis de résoudre des problèmes qui étaient autrefois inaccessibles, ouvrant la voie à des avancées significatives dans de nombreux domaines scientifiques.
Ce chapitre a illustré la méthodologie de la dérivation implicite à travers un exemple pratique et a montré son importance et ses applications dans divers domaines. Dans le chapitre suivant, nous explorerons l’optimisation des courbes et la recherche des points critiques.
Optimisation de Courbes et Points Critiques
L’optimisation est une branche fondamentale des mathématiques appliquées, essentielle pour trouver les valeurs maximales ou minimales de fonctions sous certaines contraintes. Dans ce chapitre, nous explorerons les techniques pour trouver les points critiques et optimiser les fonctions, illustrées par un exemple concret.
Techniques pour Trouver les Points Critiques
Les points critiques d’une fonction sont les points où ses dérivées partielles sont égales à zéro. Pour une fonction ![]() , les points critiques se trouvent en résolvant le système d’équations suivant :
, les points critiques se trouvent en résolvant le système d’équations suivant :
![]()
![]()
Après avoir trouvé les points critiques, nous utilisons le test de la dérivée seconde pour déterminer s’il s’agit de maximums locaux, de minimums locaux ou de points selles.
Exemple Pratique
Considérons la courbe définie par l’équation :
![]()
Nous voulons trouver le point le plus haut de la courbe, c’est-à-dire le point avec la plus grande coordonnée ![]() .
.
- Écrivons l’équation sous forme implicite :
![]()
- Trouvons les dérivées partielles de
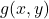 :
:
![]()
![]()
- Résolvons le système d’équations pour trouver les points critiques :
![]()
![]()
Simplifions la deuxième équation :
![]()
Substituons ![]() dans la première équation :
dans la première équation :
![]()
![]()
![]()
![]()
Donc, ![]() .
.
Nous avons trouvé un point critique à ![]() . Pour vérifier s’il s’agit d’un maximum local, d’un minimum local ou d’un point selle, nous devons analyser la courbure de la fonction en utilisant la matrice hessienne.
. Pour vérifier s’il s’agit d’un maximum local, d’un minimum local ou d’un point selle, nous devons analyser la courbure de la fonction en utilisant la matrice hessienne.
- Calculons la matrice hessienne de
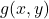 :
:
![]()
Les dérivées secondes sont :
![]()
![]()
![]()
Donc, la matrice hessienne est :
![]()
Pour déterminer la nature du point critique, nous examinons le déterminant de la matrice hessienne :
![]()
Le déterminant est positif et ![]() , indiquant que le point critique est un minimum local.
, indiquant que le point critique est un minimum local.
Applications de l’Optimisation
L’optimisation est utilisée dans de nombreux domaines, tels que l’économie pour maximiser les profits ou minimiser les coûts, et en ingénierie pour optimiser la conception de systèmes. Par exemple, les ingénieurs utilisent ces techniques pour déterminer les dimensions optimales des composants afin de minimiser le poids tout en maximisant la résistance.
Anecdotes Historiques
L’optimisation et la recherche des points critiques ont été formalisées au XIXe siècle avec les travaux de Carl Friedrich Gauss et d’autres mathématiciens. Ces techniques ont évolué pour devenir des outils puissants utilisés dans la recherche opérationnelle et l’analyse économique.
Ce chapitre a montré comment trouver les points critiques et optimiser les fonctions, illustré par un exemple concret. Dans le chapitre suivant, nous explorerons les intégrales et les séries de Maclaurin.
Intégrales et Séries de Maclaurin

Les séries de Maclaurin sont un cas particulier des séries de Taylor, utilisées pour représenter des fonctions sous forme de séries infinies autour de zéro. Elles sont particulièrement utiles pour l’évaluation des intégrales complexes. Dans ce chapitre, nous explorerons l’utilisation des séries de Maclaurin pour représenter des intégrales et illustrerons cette technique avec un exemple concret.
Développement en Série de Maclaurin
La série de Maclaurin d’une fonction ![]() est donnée par :
est donnée par :
![]()
Cette série permet de représenter des fonctions en termes de polynômes, facilitant ainsi le calcul des intégrales. Pour illustrer cette technique, considérons l’exemple suivant :
Exemple Pratique
Utilisons la série de Maclaurin de ![]() pour écrire l’intégrale suivante comme une somme d’une série infinie :
pour écrire l’intégrale suivante comme une somme d’une série infinie :
![]()
Pour ce faire, développons ![]() en série de Maclaurin :
en série de Maclaurin :
![]()
Ainsi,
![]()
L’intégrale devient :
![]()
Nous intégrons terme par terme :
![]()
Calculons chaque intégrale :
Ainsi, l’intégrale est approximée par la somme infinie :
![]()
Importance des Séries de Maclaurin
Les séries de Maclaurin sont essentielles pour l’analyse et les approximations en mathématiques. Elles permettent de simplifier des expressions complexes et sont utilisées dans divers domaines, tels que la physique pour modéliser des phénomènes naturels, et l’ingénierie pour analyser des systèmes dynamiques.
Applications Réelles
En physique, les séries de Maclaurin sont utilisées pour approximations lorsque les solutions exactes sont difficiles à obtenir. Par exemple, dans la mécanique quantique, elles sont employées pour résoudre des équations différentielles complexes. En ingénierie, elles servent à modéliser des systèmes et à prévoir leur comportement sous différentes conditions.
Anecdotes Historiques
Les séries de Maclaurin portent le nom de Colin Maclaurin, un mathématicien écossais du XVIIIe siècle, qui a généralisé le travail de Brook Taylor pour les fonctions centrées autour de zéro. Ses contributions ont permis d’étendre les méthodes d’analyse et de rendre de nombreux problèmes mathématiques plus accessibles.
Ce chapitre a montré comment les séries de Maclaurin peuvent être utilisées pour représenter des intégrales comme des sommes de séries infinies, illustré par un exemple pratique. Dans le chapitre suivant, nous explorerons les fonctions multivariables sous contraintes et les multiplicateurs de Lagrange.
Étude des Fonctions Multivariables sous Contraintes
Les fonctions multivariables et les contraintes apparaissent fréquemment dans les problèmes d’optimisation et d’analyse en mathématiques. Les multiplicateurs de Lagrange sont une technique puissante pour trouver les extrêmes locaux de fonctions de plusieurs variables soumises à des contraintes. Dans ce chapitre, nous explorerons cette méthode et illustrerons son application par un exemple concret.
Méthode des Multiplicateurs de Lagrange
La méthode des multiplicateurs de Lagrange est utilisée pour trouver les maximums et minimums de la fonction ![]() soumise à une contrainte
soumise à une contrainte ![]() . Cette méthode consiste à introduire un multiplicateur
. Cette méthode consiste à introduire un multiplicateur ![]() et à résoudre le système suivant :
et à résoudre le système suivant :
![]()
et
![]()
Exemple Pratique
Considérons la fonction suivante :
![]()
soumise à la contrainte :
![]()
Pour trouver les points extrêmes de ![]() sous cette contrainte, nous appliquons la méthode des multiplicateurs de Lagrange.
sous cette contrainte, nous appliquons la méthode des multiplicateurs de Lagrange.
- Formulons le lagrangien :
![]()
![]()
- Calculons les dérivées partielles de
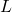 et résolvons le système :
et résolvons le système :
![]()
![]()
![]()
- Résolvons le système :
De ![]() et
et ![]() , nous avons :
, nous avons :
![]()
Substituons ![]() dans la contrainte :
dans la contrainte :
![]()
Donc, ![]() .
.
- Vérifions les points extrêmes :
Les points extrêmes sont ![]() .
.
Calculons ![]() :
:
![]()
Ainsi, le point ![]() est un minimum local pour la fonction
est un minimum local pour la fonction ![]() sous la contrainte
sous la contrainte ![]() .
.
Applications Pratiques
Les multiplicateurs de Lagrange sont largement utilisés dans divers domaines pour résoudre des problèmes d’optimisation sous contraintes. En économie, ils permettent de maximiser les fonctions de profit ou de minimiser les coûts en respectant certaines contraintes budgétaires. En physique, ils sont utilisés pour analyser des systèmes où les variables sont liées par des lois physiques.
Anecdotes Historiques
La méthode des multiplicateurs de Lagrange a été développée par Joseph-Louis Lagrange au XVIIIe siècle. Son travail a permis de formaliser les concepts d’optimisation sous contraintes, ouvrant la voie à de nombreuses applications pratiques en ingénierie et en sciences économiques.
Ce chapitre a montré comment utiliser la méthode des multiplicateurs de Lagrange pour trouver les points extrêmes de fonctions multivariables sous contraintes, illustré par un exemple pratique. Dans le chapitre suivant, nous explorerons le calcul des points critiques pour les fonctions de plusieurs variables.
Calcul des Points Critiques pour les Fonctions de Plusieurs Variables
Le calcul des points critiques pour les fonctions de plusieurs variables est essentiel pour identifier les maximums, les minimums et les points selles de ces fonctions. Dans ce chapitre, nous explorerons les méthodes pour déterminer ces points critiques et utiliserons un exemple concret pour illustrer cette technique.
Méthodes pour Trouver les Points Critiques
Les points critiques d’une fonction ![]() sont les points où les dérivées partielles de la fonction sont égales à zéro. Pour trouver ces points, nous devons résoudre le système d’équations suivant :
sont les points où les dérivées partielles de la fonction sont égales à zéro. Pour trouver ces points, nous devons résoudre le système d’équations suivant :
![]()
![]()
Après avoir trouvé les points critiques, nous utilisons la matrice hessienne pour déterminer la nature de ces points (maximum local, minimum local ou point selle).
Exemple Pratique
Considérons la fonction suivante :
![]()
Pour trouver les points critiques, nous devons calculer les dérivées partielles et résoudre le système d’équations.
- Calculons les dérivées partielles de
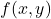 :
:
![]()
![]()
- Résolvons le système d’équations pour trouver les points critiques :
![]()
![]()
Pour la première équation, nous pouvons factoriser :
![]()
Ce qui donne deux solutions possibles :
![]()
ou
![]()
Substituons ![]() dans la deuxième équation :
dans la deuxième équation :
![]()
![]()
![]()
Ainsi, un point critique est ![]() .
.
Pour l’autre solution ![]() , substituons dans la deuxième équation :
, substituons dans la deuxième équation :
![]()
![]()
![]()
![]()
Donc,
![]()
Substituons ![]() et
et ![]() dans
dans ![]() :
:
![]()
![]()
Ainsi, les autres points critiques sont ![]() et
et ![]() .
.
- Utilisons la matrice hessienne pour déterminer la nature des points critiques :
Calculons les dérivées secondes :
![]()
![]()
![]()
La matrice hessienne est :
![]()
Pour le point critique ![]() :
:
![]()
Le déterminant est :
![]()
Le déterminant est négatif, indiquant que le point ![]() est un point selle.
est un point selle.
Pour les points critiques ![]() et
et ![]() :
:
![]()
![]()
![]()
Le déterminant est :
![]()
Le déterminant est positif et ![]() , indiquant que les points
, indiquant que les points ![]() et
et ![]() sont des maximums locaux.
sont des maximums locaux.
Applications Pratiques
Les points critiques et l’analyse de la matrice hessienne sont utilisés pour optimiser les fonctions dans divers domaines. En économie, ils permettent de trouver les prix optimaux qui maximisent les profits. En ingénierie, ces techniques sont employées pour optimiser la conception de structures et de systèmes.
Anecdotes Historiques
L’analyse des points critiques et la matrice hessienne ont été développées au XIXe siècle par des mathématiciens comme Carl Friedrich Gauss et James Clerk Maxwell. Ces concepts ont permis des avancées significatives en mathématiques appliquées et en physique.
Ce chapitre a montré comment trouver les points critiques et déterminer leur nature en utilisant la matrice hessienne, illustré par un exemple pratique. Dans le chapitre suivant, nous explorerons les intégrales multiples et leurs applications.
Intégrales Multiples et Applications
Les intégrales multiples sont un outil fondamental en analyse mathématique, particulièrement utile pour calculer des volumes et des aires sous des surfaces dans des espaces de dimensions supérieures. Dans ce chapitre, nous explorerons les techniques pour évaluer les intégrales multiples et illustrerons cette méthode avec des exemples concrets.
Techniques d’Intégration Multiple
Les intégrales doubles et triples permettent de généraliser le concept d’intégrale à des fonctions de plusieurs variables. Pour une fonction ![]() , l’intégrale double sur une région
, l’intégrale double sur une région ![]() est donnée par :
est donnée par :
![]()
Pour une fonction ![]() , l’intégrale triple sur une région
, l’intégrale triple sur une région ![]() est donnée par :
est donnée par :
![]()
Exemple Pratique
Évaluons les intégrales suivantes :
Première Intégrale
- Intégrons par rapport à
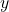 :
:
![]()
Pour simplifier cette intégrale, nous utilisons une substitution appropriée. Soit ![]() , donc
, donc ![]() et
et ![]() .
.
Quand ![]() ,
, ![]() . Quand
. Quand ![]() ,
, ![]() .
.
L’intégrale devient :
![]()
Simplifions :
![]()
![]()
- Intégrons par rapport à
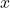 :
:
Cette intégrale est complexe et nécessite des techniques d’intégration avancées ou numériques pour être évaluée. Pour simplifier, nous pouvons utiliser des approximations ou des outils informatiques.
Deuxième Intégrale
- Intégrons par rapport à
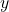 :
:
![]()
Utilisons la substitution ![]() , donc
, donc ![]() .
.
Quand ![]() ,
, ![]() . Quand
. Quand ![]() ,
, ![]() .
.
L’intégrale devient :
![]()
Simplifions :
![]()
![]()
Cette intégrale peut être évaluée pour obtenir une expression en termes de ![]() .
.
- Intégrons par rapport à
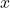 :
:
Intégrons ensuite cette expression par rapport à ![]() , en utilisant les bornes données.
, en utilisant les bornes données.
Applications des Intégrales Multiples
Les intégrales multiples sont utilisées dans divers domaines pour calculer des volumes et des aires sous des surfaces. En physique, elles permettent de déterminer les propriétés physiques des solides et des fluides. En ingénierie, elles sont utilisées pour analyser les forces et les moments dans des structures.
Anecdotes Historiques
L’utilisation des intégrales multiples remonte à des mathématiciens comme Archimède et Isaac Newton, qui ont développé des méthodes pour calculer les aires et les volumes. Ces concepts ont été formalisés au XVIIIe siècle par des mathématiciens comme Joseph-Louis Lagrange et Carl Friedrich Gauss, dont les travaux ont conduit à des avancées significatives en analyse mathématique.
Applications Réelles et Historiques des Concepts Mathématiques Avancés
Les concepts mathématiques avancés que nous avons explorés dans cet article trouvent des applications dans de nombreux domaines de la science et de l’ingénierie. Dans ce chapitre, nous examinerons quelques-unes de ces applications réelles et discuterons des contributions historiques qui ont façonné ces techniques.
Applications Réelles des Mathématiques Avancées
- Physique Théorique et Mécanique Quantique :
- Les séries de Taylor et de Maclaurin sont essentielles pour les approximations dans la mécanique quantique et d’autres domaines de la physique théorique. Par exemple, les solutions des équations de Schrödinger utilisent fréquemment ces séries pour obtenir des approximations analytiques des fonctions d’onde.
- Ingénierie et Optimisation :
- Les techniques d’optimisation, telles que la méthode des multiplicateurs de Lagrange, sont couramment utilisées en ingénierie pour maximiser l’efficacité et minimiser les coûts. Par exemple, les ingénieurs utilisent ces méthodes pour optimiser la conception de ponts, de bâtiments et d’autres structures.
- Économie et Finance :
- En économie, l’optimisation est utilisée pour maximiser les profits ou minimiser les coûts sous certaines contraintes. Les économistes utilisent des multiplicateurs de Lagrange pour analyser des modèles économiques complexes et déterminer les stratégies optimales.
- Analyse des Données et Apprentissage Automatique :
- Les dérivées implicites et les intégrales multiples sont utilisées dans l’analyse des données et l’apprentissage automatique pour optimiser les algorithmes et les modèles. Par exemple, les techniques de régression utilisent ces concepts pour ajuster les paramètres des modèles prédictifs.
- Chimie et Biologie :
- Les intégrales multiples sont utilisées en chimie pour calculer les propriétés des molécules et en biologie pour modéliser la diffusion des substances à travers les membranes cellulaires.
Contributions Historiques
Les concepts mathématiques avancés que nous utilisons aujourd’hui ont été développés au fil des siècles par de nombreux mathématiciens. Voici quelques contributions historiques notables :
- Brook Taylor :
- Brook Taylor, un mathématicien anglais du XVIIIe siècle, a développé la série de Taylor, qui est devenue un outil fondamental en analyse mathématique.
- Joseph-Louis Lagrange :
- Lagrange a apporté des contributions significatives à l’analyse mathématique et à la mécanique classique. Sa méthode des multiplicateurs de Lagrange est utilisée pour résoudre des problèmes d’optimisation sous contraintes.
- Carl Friedrich Gauss :
- Gauss, souvent appelé le « prince des mathématiciens », a contribué à de nombreux domaines des mathématiques, y compris l’analyse et la géométrie différentielle. Ses travaux sur les intégrales multiples et la théorie des surfaces ont eu un impact durable sur les mathématiques.
- Isaac Newton et Gottfried Wilhelm Leibniz :
- Newton et Leibniz sont crédités de l’invention du calcul infinitésimal, qui est à la base de nombreuses techniques mathématiques avancées que nous utilisons aujourd’hui.
- Joseph Fourier :
- Fourier a révolutionné l’analyse mathématique avec ses séries de Fourier, qui sont utilisées pour analyser les ondes et les vibrations. Ses travaux ont des applications dans des domaines allant de la musique numérique à l’imagerie médicale.
Importance des Mathématiques dans le Progrès Scientifique
Les mathématiques avancées jouent un rôle crucial dans le progrès scientifique et technologique. Elles permettent de modéliser des phénomènes complexes, d’optimiser les processus industriels et de développer de nouvelles technologies. Les techniques que nous avons explorées dans cet article sont utilisées dans la recherche scientifique, l’ingénierie, l’économie, et bien d’autres domaines pour résoudre des problèmes réels et faire avancer notre compréhension du monde.
Ce chapitre a montré comment les concepts mathématiques avancés trouvent des applications dans divers domaines et a souligné les contributions historiques qui ont façonné ces techniques. Dans le dernier chapitre, nous conclurons cet article en résumant les concepts abordés et en discutant des perspectives futures pour les mathématiques avancées.
Conclusion et Perspectives Futures
Dans cet article, nous avons exploré une variété de concepts mathématiques avancés, en examinant leur importance théorique et leurs applications pratiques. Des séries de Taylor et de Maclaurin à la dérivation implicite, en passant par les intégrales multiples et les multiplicateurs de Lagrange, nous avons vu comment ces outils puissants peuvent être utilisés pour résoudre des problèmes complexes dans divers domaines.
Résumé des Concepts Abordés
- Séries de Taylor et de Maclaurin :
- Les séries de Taylor et de Maclaurin sont utilisées pour approximer des fonctions et résoudre des limites complexes. Ces techniques sont cruciales en physique théorique et en ingénierie.
- Dérivation Implicite :
- La dérivation implicite permet de traiter des fonctions où les variables sont interdépendantes. Cette méthode est essentielle pour analyser des systèmes dynamiques en physique et en économie.
- Optimisation et Points Critiques :
- Les techniques d’optimisation, telles que les multiplicateurs de Lagrange, sont utilisées pour maximiser ou minimiser des fonctions sous contraintes. L’analyse des points critiques permet de déterminer les maximums, les minimums et les points selles.
- Intégrales Multiples :
- Les intégrales multiples sont utilisées pour calculer des volumes et des aires dans des espaces multidimensionnels. Ces techniques sont appliquées en physique, en chimie, en biologie et en ingénierie.
- Applications Réelles :
- Les concepts mathématiques avancés trouvent des applications dans de nombreux domaines, y compris la physique théorique, l’ingénierie, l’économie, l’analyse des données et bien plus encore.
Perspectives Futures
Les mathématiques avancées continueront de jouer un rôle crucial dans le progrès scientifique et technologique. Voici quelques domaines où nous pouvons nous attendre à des avancées significatives :
- Intelligence Artificielle et Apprentissage Automatique :
- Les techniques d’optimisation et les séries de Taylor et de Maclaurin sont essentielles pour développer des algorithmes d’apprentissage automatique plus efficaces. Les intégrales multiples sont utilisées pour calculer les probabilités et les distributions dans les modèles d’apprentissage profond.
- Physique Quantique et Relativité :
- Les mathématiques avancées sont indispensables pour explorer les frontières de la physique quantique et de la relativité générale. Les séries de Taylor et les dérivées implicites sont utilisées pour approximer les solutions des équations complexes qui décrivent l’univers.
- Économie et Modélisation Financière :
- Les multiplicateurs de Lagrange et les techniques d’optimisation continueront d’être utilisés pour modéliser les marchés financiers et développer des stratégies d’investissement optimales. L’analyse des données économiques nécessitera également des intégrales multiples et des dérivées implicites.
- Biologie et Chimie Computationnelles :
- Les intégrales multiples et les séries de Maclaurin seront utilisées pour modéliser les interactions moléculaires et les processus biologiques à grande échelle. Ces techniques permettront de mieux comprendre les mécanismes de la vie et de développer de nouveaux médicaments.
- Technologie et Ingénierie :
- Les techniques d’optimisation et l’analyse des points critiques seront essentielles pour concevoir des systèmes technologiques plus efficaces et durables. Les mathématiques avancées permettront de relever les défis de l’ingénierie moderne, tels que la conception de matériaux intelligents et les systèmes énergétiques renouvelables.
Conclusion
Les concepts mathématiques avancés que nous avons explorés dans cet article sont plus que de simples outils académiques. Ils sont au cœur de nombreuses innovations scientifiques et technologiques qui façonnent notre monde. En comprenant et en maîtrisant ces techniques, les étudiants et les chercheurs peuvent contribuer à résoudre les défis complexes auxquels nous sommes confrontés aujourd’hui.
Les mathématiques continueront d’évoluer, apportant de nouvelles perspectives et des solutions innovantes à des problèmes anciens. Les découvertes futures dans ce domaine promettent de transformer notre compréhension du monde et d’ouvrir de nouvelles voies pour l’exploration scientifique et technologique.
 Pourton.info
Pourton.info 



