Les Transformers, ces modèles de langage qui dominent aujourd’hui le monde de l’intelligence artificielle, sont sur toutes les lèvres. De la génération de texte à la reconnaissance d’images en passant par les assistants virtuels, ils semblent capables de tout. Mais derrière cette apparente magie se cachent des mathématiques rigoureuses, des astuces computationnelles ingénieuses et, parfois, une bonne dose de bricolage.
Dans cet article, nous allons plonger au cœur des Transformers. Pas de buzz ni de raccourcis simplistes ici : on décortiquera ensemble leur fonctionnement étape par étape, depuis la tokenisation jusqu’à leurs limites, en passant par leur utilisation dans des systèmes avancés comme les RAGs.
Alors, pourquoi ce voyage ? Parce qu’au-delà de leurs performances impressionnantes, comprendre comment fonctionnent les Transformers, c’est s’armer d’une vision critique sur leurs forces, leurs faiblesses et leurs implications pour notre monde. Et puisque la technique n’a pas à être ennuyeuse, nous adopterons un ton léger et décontracté, avec quelques touches d’humour pour rendre ce voyage encore plus agréable.
Prêt à transformer votre vision des modèles d’IA ? Suivez-moi dans ce guide complet, où les maths rencontrent la science-fiction pour révéler les secrets des Transformers.
Chapitre 1 : Tokeniser ou ne pas tokeniser, telle est la question

Avant de plonger dans les abysses mathématiques des Transformers, il faut comprendre une étape fondamentale : la tokenisation. Si les Transformers étaient des chefs étoilés, la tokenisation serait l’équivalent de préparer les ingrédients avant de cuisiner. On découpe, on trie, on ordonne. Mais ici, au lieu de légumes, on manipule… des mots, des morceaux de mots, et même parfois des lettres.
C’est quoi un token ?
Un token, c’est une unité de base d’information. Cela peut être :
- Un mot entier : « mathématiques »
- Un morceau de mot : « mathé » et « matiques »
- Un caractère isolé : « m », « a », « t »…
Prenons une phrase simple pour illustrer :
« Transformer, c’est génial ! »
Après tokenisation, cela pourrait donner quelque chose comme :
- [« Transformer », « , », « c », « ‘ », « est », « génial », « ! »]
Pourquoi découper en tokens ?
Les Transformers ne comprennent pas le langage humain. Ils préfèrent jongler avec des chiffres. La première étape consiste donc à convertir les phrases en tokens. Chaque token se voit ensuite attribuer un identifiant numérique. Pour un modèle comme LLaMA 3, cela signifie travailler avec un dictionnaire gigantesque de 128 000 tokens possibles. Autant dire qu’il y a de quoi s’amuser.
Comment ça marche ?
Le processus de tokenisation repose sur des algorithmes d’apprentissage. Ils apprennent à décomposer les phrases de manière optimale pour maximiser la représentation des données. Supposons que nous avons une phrase de 5 mots. Après tokenisation, cela pourrait donner une séquence de, disons, 12 tokens (certains mots étant décomposés).
Pour une phrase donnée, la sortie sera donc une séquence d’identifiants numériques, que nous noterons ainsi :
![]()
où ![]() représente l’identifiant du i-ème token, et
représente l’identifiant du i-ème token, et ![]() est le nombre total de tokens.
est le nombre total de tokens.
Petit exemple concret :
Prenons une phrase comme :
« La physique, c’est incroyable. »
Après tokenisation, cela pourrait donner :
- Séquence initiale : [« La », « physique », « , », « c », « ‘ », « est », « incroyable », « . »]
- Séquence d’identifiants :
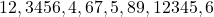
Ces identifiants servent ensuite de point d’entrée pour les opérations mathématiques dans le Transformer.
Et les limites ?
Le tokenizer n’est pas parfait. Il peut produire des résultats peu intuitifs. Par exemple, un mot rare ou un néologisme peut être découpé en plusieurs morceaux peu significatifs. Si on entre « Transformerisation », cela pourrait donner :
- [« Transformer », « isation »]
Cela dit, cette étape est cruciale, car elle pose les bases pour tout ce qui suit.
Chapitre 2 : 128 000 tokens : Quand la soupe à l’alphabet devient une matrice XXL

Maintenant que vos phrases sont découpées en tokens et converties en une séquence d’identifiants, il est temps de les plonger dans l’univers des mathématiques : les matrices. C’est ici que les choses deviennent sérieuses. Ces identifiants numériques, pour l’instant assez abstraits, vont être transformés en vecteurs bien définis dans un espace mathématique, grâce à un outil magique : la matrice des représentations vectorielles des tokens, aussi appelée matrice d’embeddings.
Pourquoi des vecteurs ?
Les Transformers adorent travailler avec des vecteurs et des matrices, car cela permet d’appliquer facilement des opérations mathématiques optimisées (merci les GPU !). Chaque token sera donc représenté par un vecteur dans un espace de grande dimension. Par exemple, pour LLaMA 3, cet espace a une dimension de 16 384. Cela signifie que chaque token est traduit en un point de cet espace, comme si on plaçait un mot dans une galaxie en 16 384 dimensions. Rien que ça.
La matrice des embeddings : la carte de l’univers des tokens
Imaginez une énorme table où chaque ligne représente un token et chaque colonne une des dimensions de l’espace vectoriel. Cette table est en réalité une matrice, notée ![]() , dont les dimensions sont :
, dont les dimensions sont :
![]()
où :
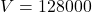 est le nombre total de tokens possibles (taille du vocabulaire),
est le nombre total de tokens possibles (taille du vocabulaire),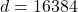 est la dimension de l’espace vectoriel.
est la dimension de l’espace vectoriel.
Pour un token d’identifiant ![]() , sa représentation vectorielle correspond à la
, sa représentation vectorielle correspond à la ![]() -ième ligne de cette matrice, notée :
-ième ligne de cette matrice, notée :
![]()
Un exemple pour illustrer :
Prenons la phrase déjà tokenisée :
- Identifiants :
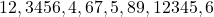
Grâce à la matrice des embeddings, chaque identifiant sera transformé en un vecteur de dimension ![]() . La séquence devient alors :
. La séquence devient alors :
![]()
Chaque ![]() est un vecteur de dimension 16 384. En regroupant ces vecteurs, on obtient une matrice de représentation du texte, notée
est un vecteur de dimension 16 384. En regroupant ces vecteurs, on obtient une matrice de représentation du texte, notée ![]() , qui a les dimensions suivantes :
, qui a les dimensions suivantes :
![]()
où :
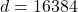 , la dimension de l’espace vectoriel,
, la dimension de l’espace vectoriel,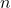 , le nombre de tokens dans la séquence (ici 8).
, le nombre de tokens dans la séquence (ici 8).
Visualiser cette matrice XXL
Si on voulait la voir (et si nos cerveaux pouvaient gérer autant de dimensions), cela ressemblerait à une gigantesque grille, chaque colonne représentant un token dans l’espace vectoriel. Concrètement, cette matrice ![]() encapsule toute l’information initiale du texte d’entrée sous une forme mathématique prête à être manipulée par le Transformer.
encapsule toute l’information initiale du texte d’entrée sous une forme mathématique prête à être manipulée par le Transformer.
À quoi sert cette transformation ?
En convertissant les tokens en vecteurs, le modèle peut :
- Appliquer des opérations linéaires comme des multiplications matricielles pour extraire des relations.
- Utiliser ces représentations pour capter des patterns complexes entre les tokens.
Mais est-ce magique ?
Non, car la matrice des embeddings ![]() n’est pas créée au hasard. Elle est optimisée pendant l’entraînement du modèle. Chaque ligne est ajustée pour que les tokens proches dans leur signification aient des vecteurs proches dans cet espace. Par exemple, les mots « chat » et « chien » pourraient avoir des vecteurs proches, alors que « chat » et « moteur » seraient plus éloignés.
n’est pas créée au hasard. Elle est optimisée pendant l’entraînement du modèle. Chaque ligne est ajustée pour que les tokens proches dans leur signification aient des vecteurs proches dans cet espace. Par exemple, les mots « chat » et « chien » pourraient avoir des vecteurs proches, alors que « chat » et « moteur » seraient plus éloignés.
Chapitre 3 : Transformer Blocks : Les Lego du futur (en beaucoup plus compliqué)

Les Transformer Blocks sont au cœur de la puissance des Transformers. Si vous imaginez les Transformers comme un gratte-ciel mathématique, chaque étage serait un bloc Transformer, chargé de modifier progressivement les représentations vectorielles des tokens pour les rendre de plus en plus intelligentes. Et oui, on construit l’intelligence couche par couche !
De quoi est fait un bloc Transformer ?
Un bloc Transformer est composé de deux éléments principaux, qui travaillent en tandem comme des mécaniciens de l’information :
- Le module d’attention multi-tête : il permet aux tokens de « discuter » entre eux.
- Le réseau feed-forward : il ajuste les vecteurs de chaque token individuellement, sans interférence des autres.
Ces deux modules sont entourés d’opérations de normalisation pour maintenir la stabilité des calculs. Le tout est arrangé comme suit :
- Entrée → Attention multi-tête → Normalisation → Feed-forward → Normalisation → Sortie.
Étape 1 : L’attention multi-tête
L’objectif principal de l’attention est de permettre à chaque token de regarder tous les autres tokens de la séquence et de déterminer ceux qui sont les plus pertinents pour lui. En mathématiques, cela se traduit par le calcul de scores d’attention entre chaque paire de tokens.
Le processus peut être résumé ainsi :
- Représentations d’entrée : Chaque token est représenté par un vecteur
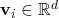 .
. - Calcul des scores d’attention : Pour chaque paire de tokens
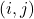 , on calcule un score basé sur un produit scalaire :
, on calcule un score basé sur un produit scalaire :
![]()
où :
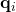 (query) est une projection linéaire de
(query) est une projection linéaire de 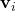 ,
,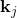 (key) est une projection linéaire de
(key) est une projection linéaire de 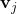 .
.
Normalisation des scores : Les scores sont normalisés avec une opération softmax pour produire des poids d’attention :
![]()
Combinaison des informations : Chaque token ![]() reçoit une combinaison pondérée des vecteurs projetés des autres tokens (les values) :
reçoit une combinaison pondérée des vecteurs projetés des autres tokens (les values) :
![]()
Attention multi-tête : Ce processus est répété plusieurs fois en parallèle, chaque « tête » ayant ses propres matrices de projection pour ![]() ,
, ![]() et
et ![]() .
.
Le résultat final est une nouvelle représentation de chaque token, enrichie par les informations pertinentes provenant des autres tokens.
Étape 2 : Le réseau feed-forward
Après l’attention, chaque token passe par un réseau feed-forward, qui agit comme une fonction non-linéaire pour ajuster ses vecteurs. Le processus est le suivant :
- Chaque vecteur
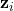 est transformé par une série de couches linéaires et non-linéaires :
est transformé par une série de couches linéaires et non-linéaires : 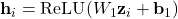
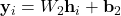 où :
où :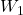 et
et 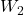 sont des matrices de poids,
sont des matrices de poids,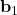 et
et 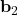 sont des vecteurs de biais,
sont des vecteurs de biais,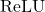 est une fonction d’activation non-linéaire.
est une fonction d’activation non-linéaire.
- Enfin, on ajoute une connexion résiduelle, c’est-à-dire qu’on additionne la sortie
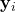 avec l’entrée initiale
avec l’entrée initiale 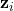 :
:
![]()
Cette connexion résiduelle aide à éviter les problèmes de gradients vanissants dans les réseaux très profonds.
Un bloc Transformer complet
Mettons tout cela ensemble : un bloc Transformer prend en entrée une matrice ![]() (la représentation initiale des tokens) et produit une matrice de même taille, mais avec des vecteurs enrichis d’informations contextuelles.
(la représentation initiale des tokens) et produit une matrice de même taille, mais avec des vecteurs enrichis d’informations contextuelles.
Après une couche, la matrice est transformée en :
![]()
Chaque couche affine un peu plus la compréhension contextuelle des tokens. Avec 126 couches, autant dire que les tokens deviennent de vrais petits génies à la fin.
Chapitre 4 : Attention, Attention ! (Non, vraiment, c’est important)

Le secret du succès des Transformers réside dans leur mécanisme d’attention. Plus précisément, l’attention multi-tête (multi-head attention), qui permet aux tokens de « regarder autour d’eux » pour comprendre le contexte. C’est un peu comme dans une classe où chaque élève peut échanger des informations avec ses camarades pour mieux comprendre le sujet… sauf que certains élèves sont plus « intéressants » que d’autres.
Pourquoi l’attention ?
Quand on lit une phrase, on ne se concentre pas seulement sur le mot précédent, mais sur tout ce qui précède pour en saisir le sens. L’attention imite ce processus en permettant à chaque token de se connecter avec tous les autres tokens dans la séquence.
Prenons une phrase simple :
« La physique quantique est fascinante. »
Pour comprendre que « fascinante » qualifie « physique quantique », un Transformer doit être capable de relier ces mots malgré la distance qui les sépare.
Les étapes de l’attention :
L’attention multi-tête repose sur un processus en trois étapes, avec des concepts clés : query, key, et value (souvent abrégés en Q, K, V). Voici comment cela fonctionne :
- Projections linéaires des tokens : Chaque vecteur d’entrée
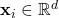 (le vecteur associé au token
(le vecteur associé au token 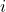 ) est projeté dans trois espaces différents :
) est projeté dans trois espaces différents :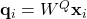 (query)
(query)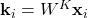 (key)
(key)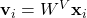 (value)
(value)
Ici,
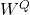 ,
, 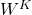 , et
, et 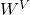 sont des matrices de projection (apprises pendant l’entraînement), chacune de dimensions
sont des matrices de projection (apprises pendant l’entraînement), chacune de dimensions 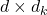 , où
, où 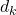 est la dimension des espaces réduits.
est la dimension des espaces réduits. - Calcul des scores d’attention : Les queries et les keys permettent de calculer un score qui mesure à quel point deux tokens sont liés. Ce score est obtenu par un produit scalaire entre
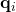 et
et
![]()
:
![]()
- Le terme
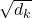 est une normalisation pour éviter que les scores explosent lorsque
est une normalisation pour éviter que les scores explosent lorsque 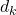 est grand.
est grand.
Normalisation des scores avec Softmax : Les scores ![]() sont transformés en probabilités avec une fonction Softmax :
sont transformés en probabilités avec une fonction Softmax :
![]()
Le poids ![]() indique à quel point le token
indique à quel point le token ![]() influence le token
influence le token ![]() .
.
Combinaison pondérée des values : Une fois les poids calculés, chaque token ![]() reçoit une combinaison pondérée des vecteurs
reçoit une combinaison pondérée des vecteurs
![]()
(les values) :
![]()
Le résultat ![]() est la nouvelle représentation enrichie du token
est la nouvelle représentation enrichie du token ![]() , prenant en compte le contexte fourni par les autres tokens.
, prenant en compte le contexte fourni par les autres tokens.
Attention multi-tête : L’art de voir sous plusieurs angles
Au lieu d’utiliser une seule projection Q, K, V, le Transformer en utilise plusieurs, appelées têtes d’attention. Chaque tête apprend à se concentrer sur des aspects différents du contexte.
Si nous avons ![]() têtes, le processus est le suivant :
têtes, le processus est le suivant :
- Chaque tête calcule sa propre version de
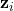 avec des matrices
avec des matrices 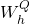 ,
, 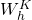 , et
, et 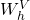 .
. - Les résultats sont concaténés pour former un vecteur de dimension
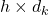 .
. - Ce vecteur est projeté dans l’espace initial
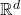 grâce à une matrice finale
grâce à une matrice finale 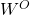 .
.
Formule globale de l’attention multi-tête :
Le résultat final pour tous les tokens peut être résumé comme suit : ![]()
où :
![]()
Pourquoi tout ce travail ?
Grâce à ce mécanisme, les Transformers peuvent :
- Identifier les relations entre tokens proches ou éloignés dans la séquence.
- Manipuler l’information en parallèle grâce aux multiples têtes d’attention.
C’est cette capacité à capter les dépendances complexes qui fait des Transformers une architecture si puissante.
Chapitre 5 : Softmax : Quand les maths deviennent douces et probables

La fonction Softmax est l’un des outils les plus élégants et pratiques de l’arsenal mathématique des Transformers. Si vous deviez la résumer, ce serait : elle transforme des scores bruts en probabilités lisses. Mais pourquoi est-ce si important ? Regardons cela en détail.
À quoi sert Softmax ?
Imaginons que nous avons calculé des scores d’attention entre un token donné et tous les autres tokens d’une séquence. Ces scores, notés ![]() , peuvent être n’importe quel nombre réel, positif ou négatif. Mais pour interpréter ces scores, il faut les normaliser de manière à ce qu’ils :
, peuvent être n’importe quel nombre réel, positif ou négatif. Mais pour interpréter ces scores, il faut les normaliser de manière à ce qu’ils :
- Tombent dans l’intervalle [0, 1],
- Somment à 1 (comme des probabilités).
C’est exactement ce que fait Softmax. Elle prend un vecteur de scores ![]() et produit un vecteur de probabilités
et produit un vecteur de probabilités ![]() , où :
, où :
![]()
Pourquoi utiliser l’exponentielle ?
La fonction exponentielle ![]() a plusieurs propriétés intéressantes :
a plusieurs propriétés intéressantes :
- Elle est toujours positive : peu importe si
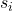 est négatif,
est négatif, 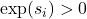 .
. - Elle amplifie les écarts : si deux scores diffèrent légèrement, leurs exponentielles auront un écart plus important, ce qui aide à accentuer les différences.
- Elle garantit une « compétition » naturelle : les scores les plus élevés deviennent proportionnellement plus importants.
Prenons un exemple concret :
- Scores bruts :
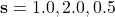
- Exponentielles :
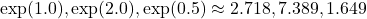
- Softmax :
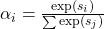 , donc :
, donc : 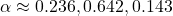
Résultat : le score ![]() domine (64 %), mais les autres scores ne sont pas complètement ignorés.
domine (64 %), mais les autres scores ne sont pas complètement ignorés.
Softmax et l’attention :
Dans un module d’attention, Softmax transforme les scores ![]() en poids d’attention
en poids d’attention ![]() , représentant à quel point le token
, représentant à quel point le token ![]() influence le token
influence le token ![]() .
.
Rappelons la formule des poids d’attention :
![]()
Ici :
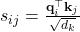 , le score brut entre les tokens
, le score brut entre les tokens 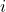 et
et 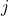 .
.- La somme dans le dénominateur garantit que les poids sont normalisés.
Propriétés intéressantes de Softmax :
- Lissage des résultats :
- Même un score faible obtient une petite probabilité (jamais exactement 0), ce qui évite d’ignorer complètement certaines informations.
- Sensibilité aux différences :
- Si un score est très supérieur aux autres, Softmax lui attribue une probabilité dominante, amplifiant les relations fortes.
- Robustesse mathématique :
- Softmax est différentiable, ce qui est essentiel pour l’entraînement des modèles par descente de gradient.
Limites de Softmax :
Malgré sa puissance, Softmax n’est pas parfaite :
- Sensibilité aux grandes valeurs : Si les scores bruts sont très grands, leurs exponentielles peuvent entraîner des problèmes numériques (overflow). Cela est parfois corrigé en soustrayant une constante
 :
:
![]()
Où ![]() pour stabiliser les calculs.
pour stabiliser les calculs.
Concentration excessive : Si les scores bruts ont des écarts énormes, Softmax tend à attribuer presque toute la probabilité à un seul score.
En résumé :
Softmax est l’étape qui transforme des scores bruts en une probabilité claire et exploitable. Dans les Transformers, elle agit comme un « juge » qui décide comment chaque token influence les autres. Sans elle, les poids d’attention seraient désordonnés, et le modèle ne pourrait pas capter efficacement les relations contextuelles.
Chapitre 6 : Décodez ça, si vous pouvez !

Après avoir traversé le labyrinthe des Transformers, nos tokens doivent enfin retrouver leur forme originale, ou presque. C’est là qu’intervient une étape cruciale : la décodage ou détokenisation. Cette phase transforme la matrice des probabilités générées en une séquence de tokens, puis en texte compréhensible. C’est le moment où les mathématiques rencontrent la poésie (ou pas, selon la qualité de l’entraînement…).
Revenons à notre matrice de probabilités
À l’issue des 126 couches de LLaMA 3, chaque colonne de la matrice finale contient une représentation sophistiquée du contexte. Grâce à des transformations supplémentaires, chaque colonne est projetée dans un espace de dimension égale au vocabulaire ![]() (ici,
(ici, ![]() ).
).
La matrice finale a donc pour dimensions :
![]()
où :
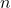 est le nombre de positions (tokens) dans la séquence.
est le nombre de positions (tokens) dans la séquence.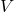 est la taille du vocabulaire.
est la taille du vocabulaire.
Chaque ligne de ![]() représente une distribution de probabilités sur tous les tokens possibles. Ces probabilités indiquent la « confiance » du modèle dans les tokens suivants possibles.
représente une distribution de probabilités sur tous les tokens possibles. Ces probabilités indiquent la « confiance » du modèle dans les tokens suivants possibles.
Comment choisir le prochain token ?
À chaque position, on choisit un token en fonction de sa probabilité. Cela peut se faire de plusieurs façons :
- Méthode déterministe (argmax) : On choisit le token avec la probabilité la plus élevée :
![]()
Cette méthode est simple, mais elle peut rendre le texte trop prévisible et monotone.
Méthode stochastique (échantillonnage) : On tire un token au hasard selon les probabilités :
- Si
![Rendered by QuickLaTeX.com P[i, :] = {0.1, 0.7, 0.2}](https://pourton.info/wp-content/ql-cache/quicklatex.com-060b722966bed396b467ffad486cc0aa_l3.png) , alors le second token a 70 % de chances d’être sélectionné. Cette approche produit des textes plus variés et naturels, mais aussi plus risqués (gare aux incohérences !).
, alors le second token a 70 % de chances d’être sélectionné. Cette approche produit des textes plus variés et naturels, mais aussi plus risqués (gare aux incohérences !).
Méthodes avancées (température, top-k, nucleus sampling) :
- Température : On ajuste la distribution en élevant les probabilités à une puissance
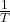 , où
, où 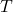 est la température. Une température basse (proche de 0) rend les choix plus conservateurs, tandis qu’une température élevée favorise l’exploration.
est la température. Une température basse (proche de 0) rend les choix plus conservateurs, tandis qu’une température élevée favorise l’exploration. - Top-k : On ne considère que les
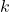 tokens les plus probables, en ignorant les autres.
tokens les plus probables, en ignorant les autres. - Nucleus sampling : Similaire au top-k, mais on sélectionne les tokens jusqu’à ce que la somme des probabilités atteigne un certain seuil
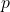 .
.
Répéter jusqu’à la fin
Une fois le token suivant choisi, il est ajouté à la séquence, et le modèle répète le processus en mettant à jour son contexte avec le nouveau token.
Par exemple, si la séquence initiale est : « Les mathématiques sont » Le modèle peut générer successivement : « Les mathématiques sont fascinantes et » « Les mathématiques sont fascinantes et complexes. »
Ce processus continue jusqu’à ce qu’une condition d’arrêt soit atteinte, comme :
- La génération d’un token spécial de fin (
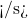 ).
). - Une longueur maximale.
La magie de la détokenisation
Une fois tous les tokens générés, leur séquence est convertie en texte lisible grâce au tokenizer inverse, qui traduit les identifiants numériques en mots, morceaux de mots, ou caractères. Par exemple :
- Tokens :
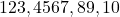
- Texte : « Transformer, c’est fascinant. »
Ce processus semble simple, mais il repose sur la précision du tokenizer initial. Une mauvaise tokenisation en amont peut conduire à des erreurs ou des incohérences lors de la détokenisation.
Un défi pour les Transformers
Le décodage est un équilibre délicat entre cohérence et créativité. Trop conservateur, le modèle produit un texte banal et rigide. Trop aventureux, il peut partir dans des délires incohérents. Trouver le bon réglage est donc une science autant qu’un art.
Chapitre 7 : Transformers et Multimodalité : Textes, images, sons… et demain ?

Les Transformers, dans leur version standard, sont conçus pour traiter du texte. Mais les chercheurs n’en sont pas restés là : ils ont étendu cette architecture à d’autres types de données comme les images, les sons, et même les vidéos. C’est ce qu’on appelle la multimodalité, une capacité des modèles à jongler avec plusieurs formats d’information.
Le principe de la multimodalité
La multimodalité consiste à intégrer différents types de données dans un même modèle pour qu’il puisse les comprendre et les utiliser conjointement. Par exemple :
- Analyser une image tout en lisant une description associée.
- Écouter une voix et interpréter son contenu textuel.
- Générer du texte basé sur une vidéo ou une combinaison des deux.
En pratique, cela implique d’ajouter des modules capables de transformer ces nouveaux types de données (sons, images, vidéos) en représentations mathématiques compatibles avec les blocs Transformers.
Le cas des images
Pour inclure des images, l’idée est de transformer chaque image en une séquence de tokens, tout comme on le fait pour le texte. Cela passe souvent par :
- Découper l’image en petits morceaux : On divise une image en patchs de
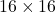 pixels, par exemple.
pixels, par exemple. - Transformer chaque patch en un vecteur : On utilise un réseau de convolution ou un encodeur visuel pour produire un vecteur
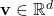 pour chaque patch.
pour chaque patch. - Traiter les vecteurs comme des tokens : Ces vecteurs deviennent l’entrée du Transformer, qui les manipule comme des tokens textuels.
Au final, une image est représentée par une matrice ![]() de taille
de taille ![]() , où
, où ![]() est le nombre de patchs.
est le nombre de patchs.
Le cas des sons
Pour le son (et particulièrement la voix), le processus est similaire :
- Extraction de caractéristiques audio : On utilise un encodeur vocal pour extraire des vecteurs à partir du signal sonore, souvent en analysant des spectrogrammes.
- Conversion en séquence de tokens : Ces vecteurs sont ensuite transformés en une séquence mathématique manipulable par les blocs Transformers.
Exemple : Si on entre un fichier audio disant « Bonjour », le modèle transforme le signal sonore en une séquence de tokens textuels avant de les traiter.
L’intégration dans les Transformers
Une fois les données transformées en tokens, elles peuvent être combinées avec du texte grâce à un mécanisme spécifique : l’attention croisée. Ce module permet aux représentations issues d’un format (par exemple, des images) d’interagir avec celles d’un autre format (par exemple, du texte). Voici comment cela fonctionne :
- Chaque type de données (texte, image, son) passe par un encodeur spécifique.
- Les représentations issues des différents encodeurs sont combinées à l’aide de modules d’attention croisée.
- Le Transformer apprend à connecter les informations issues des différents formats.
Un exemple concret : ChatGPT vision
ChatGPT vision, une version multimodale des Transformers, peut traiter à la fois du texte et des images. Si on lui montre une image d’un chat avec une légende « Qu’est-ce que c’est ? », il analyse l’image et le texte pour répondre « C’est un chat ! ».
Cela repose sur une interaction entre les représentations vectorielles de l’image et du texte dans le modèle. C’est comme si les vecteurs issus de l’image et du texte « discutaient » pour trouver une réponse commune.
Et demain ?
La multimodalité ne s’arrête pas là. Les chercheurs explorent des applications encore plus complexes, comme :
- Générer une vidéo à partir d’une description textuelle.
- Fusionner des données médicales (imagerie, rapports) pour diagnostiquer des maladies.
- Faire collaborer des robots à partir d’instructions écrites et d’analyses visuelles.
Les défis de la multimodalité
Bien que prometteuse, la multimodalité pose de nombreux défis :
- Coût en calcul : Intégrer plusieurs formats de données demande une puissance de calcul énorme.
- Alignement des données : Il est difficile de synchroniser correctement des informations de nature différente.
- Problèmes éthiques : Les modèles multimodaux peuvent être utilisés à des fins nuisibles, comme créer de fausses vidéos (deepfakes).
Chapitre 8 : Des maths à la NSA : Pourquoi vos conversations avec ChatGPT ne sont jamais vraiment privées

Maintenant que nous avons vu comment les Transformers fonctionnent et s’adaptent à différents formats, intéressons-nous à une question sensible : la sécurité des données. Si les Transformers sont si puissants, cela signifie qu’ils retiennent et apprennent énormément d’informations. Mais qu’advient-il de ces données ? Et surtout, qu’est-ce que cela implique pour votre vie privée ?
Les Transformers : de véritables éponges à données
Lorsqu’un Transformer est entraîné, il consomme une quantité astronomique de données. Ces données incluent souvent :
- Des livres.
- Des sites web.
- Des conversations (dans le cas des chatbots).
- Et parfois, des informations sensibles issues de bases de données mal contrôlées.
Le modèle utilise ces données pour ajuster ses milliards de paramètres. Cela signifie que, dans certaines circonstances, les informations contenues dans ces données d’entraînement peuvent être « mémorisées » par le modèle.
Exemple concret : Si un Transformer est entraîné sur une phrase contenant votre numéro de téléphone, il pourrait théoriquement reproduire cette information lorsqu’un utilisateur pose une question qui s’en rapproche.
Pourquoi les données sensibles posent problème
Les Transformers ne font pas la différence entre une donnée sensible et une information publique. Ils traitent tout comme un texte brut, optimisé pour la génération. Cela pose plusieurs problèmes majeurs :
- Mémorisation accidentelle : Même si l’entraînement vise à éviter une mémorisation excessive, il peut arriver que des fragments de données sensibles soient retenus.
- Risque d’extraction de données : Un utilisateur malintentionné pourrait formuler des requêtes spécifiques pour extraire des données confidentielles du modèle, un phénomène connu sous le nom de prompt injection.
La paranoïa des organisations gouvernementales
Des institutions comme la NSA ou d’autres agences de renseignement ont rapidement compris le potentiel (et les risques) des modèles de langage. Ces organisations surveillent de près :
- Les données utilisées pour entraîner les modèles.
- Les entreprises qui gèrent ces modèles.
- Et, évidemment, les interactions entre les utilisateurs et ces systèmes.
Le danger, c’est que les entreprises qui développent ces modèles peuvent être contraintes de partager des données ou des résultats avec ces agences dans certains pays. En d’autres termes : vos conversations avec un chatbot pourraient ne pas être aussi privées que vous le pensez.
Comment les fournisseurs essaient de se protéger
Pour limiter ces risques, plusieurs mesures ont été mises en place :
- Filtrage des données d’entraînement : Exclure les bases de données contenant des informations personnelles identifiables.
- Anonymisation : Remplacer les noms, numéros et adresses par des tokens génériques avant l’entraînement.
- Encadrement légal : Les entreprises doivent respecter des lois comme le RGPD (en Europe), qui imposent des règles strictes sur l’utilisation des données personnelles.
Est-ce suffisant ?
Pas vraiment. Les grands modèles de langage restent des boîtes noires. Même leurs concepteurs ne savent pas exactement quelles informations sont retenues ou oubliées. Cela signifie qu’un utilisateur prudent devrait toujours considérer que :
- Une interaction avec un chatbot peut être enregistrée.
- Les informations sensibles ne devraient jamais être partagées avec ces outils.
Une comparaison pour mieux comprendre
Imaginez un Transformer comme un étudiant en examen :
- Il mémorise autant qu’il peut pendant ses révisions.
- Lors de l’examen (lorsqu’il génère du texte), il peut reproduire des morceaux appris, même par erreur.
- Mais il ne comprend pas vraiment ce qu’il récite.
Conclusion pragmatique
Les Transformers sont incroyablement utiles, mais leur fonctionnement soulève des questions fondamentales sur la vie privée et la sécurité des données. Tant que leur apprentissage restera aussi massif et incontrôlé, il faudra être vigilant. En d’autres termes : ne dites rien à ChatGPT que vous ne voudriez pas voir sur la place publique !
Chapitre 9 : Les Transformers, un miracle… ou juste un joli bricolage ?

Les Transformers, malgré leurs performances impressionnantes, ne sont pas des entités magiques. Leur succès repose sur une combinaison d’astuces mathématiques et d’optimisations computationnelles qui, ensemble, donnent l’illusion d’une intelligence exceptionnelle. Mais qu’en est-il vraiment ? Décryptons leurs forces et leurs limites.
Pourquoi les Transformers brillent-ils autant ?
Les Transformers sont devenus l’architecture dominante dans le domaine du traitement du langage naturel (NLP) et bien au-delà. Voici les principales raisons de leur succès :
- Parallélisation efficace : Contrairement aux réseaux récurrents (RNN), qui traitent les séquences mot par mot, les Transformers traitent toutes les positions simultanément grâce à leur architecture basée sur l’attention. Cela permet d’exploiter pleinement les capacités des GPU modernes.
- Capacité à capter le contexte : Grâce à l’attention multi-tête, les Transformers peuvent analyser les relations entre des mots éloignés dans une phrase, ce que les modèles traditionnels avaient du mal à faire.
- Taille colossale : Avec des milliards de paramètres, les Transformers ont une capacité sans précédent pour mémoriser et généraliser des informations.
- Robustesse des mathématiques : Leur structure différentiable permet un apprentissage efficace grâce à la descente de gradient stochastique.
Mais pourquoi tout ce bricolage ?
Malgré leur puissance, les Transformers utilisent des astuces qui cachent certaines faiblesses fondamentales :
- Mémoire limitée : Les Transformers ne traitent qu’un nombre limité de tokens à la fois (par exemple, 4 096 pour certains modèles), ce qui peut poser problème avec des documents très longs.
- Approximation de la compréhension : Ils n’ont pas de véritable compréhension sémantique ; ils se contentent d’imiter des patterns appris.
- Coût énergétique : Entraîner un Transformer comme GPT-4 nécessite des ressources colossales, ce qui soulève des questions sur la durabilité écologique.
Un modèle intelligent ou un perroquet stochastique ?
Un Transformer ne « comprend » pas. Il prédit le mot ou le token suivant en se basant sur les probabilités calculées à partir des données d’entraînement. Cela le rend incroyablement performant dans des tâches spécifiques, mais il manque de plusieurs capacités cognitives humaines :
- Pas de raisonnement abstrait : Il n’infère pas de vérités universelles ; il exploite des corrélations.
- Pas de mémoire réelle : Chaque requête est traitée indépendamment, sans « mémoire à long terme » des conversations passées.
- Pas de conscience ni d’intentionnalité : Les Transformers ne « veulent » rien, ils appliquent des calculs.
Un succès malgré des fondations fragiles
Ce qui rend les Transformers performants n’est pas leur compréhension profonde, mais une série d’optimisations bien pensées :
- Normalisation des vecteurs : On divise les vecteurs par leur norme pour éviter des explosions ou des effondrements des gradients.
- Des heuristiques comme le Softmax : Elle permet de convertir des scores en probabilités bien normalisées.
- Des solutions pour contourner les limitations : Des techniques comme la fenêtre glissante permettent de traiter des textes plus longs.
Les limites actuelles des Transformers
- Robustesse limitée : Les Transformers sont sensibles aux inputs inattendus. Par exemple, des phrases absurdes ou des prompts biaisés peuvent produire des résultats incohérents.
- Manque d’explicabilité : Pourquoi le modèle choisit-il tel ou tel mot ? Les chercheurs peinent encore à répondre à cette question, car le fonctionnement interne des Transformers reste une boîte noire.
- Applications adversariales : Les Transformers sont vulnérables aux attaques comme les « adversarial prompts », où des entrées conçues intentionnellement induisent des erreurs.
Alors, miracle ou bricolage ?
Les Transformers ne sont ni miraculeux ni inutiles. Leur efficacité est indéniable dans de nombreux domaines, mais ils ne sont qu’un outil. Leur compréhension limitée les rend inadaptés à des situations nécessitant de la vraie réflexion ou une prise de décision autonome. Cela dit, comme tout bon bricolage, ils fonctionnent étonnamment bien quand ils sont entre de bonnes mains.
Chapitre 10 : Quand les matrices s’emmêlent : Pourquoi les Transformers ne sont pas encore prêts pour l’apocalypse IA

Les Transformers impressionnent par leur capacité à générer du texte fluide, à analyser des données complexes et à s’adapter à de nombreux contextes. Mais malgré cette aura presque mystique, ils sont encore loin d’être prêts à déclencher une apocalypse IA. En réalité, ils sont bardés de limitations, qu’il est utile de décortiquer pour garder les pieds sur terre.
Problème n°1 : La dépendance à la taille des données
Les Transformers ont une appétit vorace pour les données. Leur succès repose sur des bases de données gigantesques, couvrant des milliards de phrases, de mots, et de contextes. Cependant :
- Qualité vs quantité : Beaucoup des données disponibles sur Internet sont biaisées, incorrectes ou redondantes.
- Limites éthiques : Les Transformers peuvent absorber des données sensibles ou protégées par des droits d’auteur, soulevant des questions juridiques et morales.
Sans cette masse de données, les Transformers sont comme des voitures de course sans carburant. Leur dépendance extrême aux données les rend inefficaces dans des contextes où l’information est rare ou incomplète.
Problème n°2 : La mémoire courte
Les Transformers ont une capacité limitée à traiter de longues séquences de texte. Par exemple, un modèle peut n’analyser que 4 096 tokens à la fois, ce qui représente environ 3 pages de texte. Au-delà, ils doivent tronquer ou utiliser des astuces comme des fenêtres glissantes, ce qui peut causer des pertes de contexte cruciales.
Prenons un exemple simple :
- Si un Transformer lit un roman, il ne se souvient pas du premier chapitre lorsqu’il rédige le dernier. Cela peut nuire à la cohérence globale.
Problème n°3 : Le manque de compréhension sémantique
Les Transformers fonctionnent par corrélation statistique, pas par compréhension réelle. Cela signifie qu’ils peuvent produire des réponses absurdes ou incohérentes dans des contextes complexes. Par exemple :
- Question : « Quelle est la couleur du cheval blanc d’Henri IV ? »
- Réponse possible : « Le cheval blanc est une race célèbre en Europe. »
Le modèle peut mélanger des informations correctes et incorrectes parce qu’il ne comprend pas vraiment la question.
Problème n°4 : La sensibilité aux perturbations
Un Transformer peut être facilement déstabilisé par de petites modifications dans l’entrée. Par exemple :
- « ChatGPT est génial. » produit une réponse sensée.
- « ChatGPT est génial!! » (avec deux points d’exclamation) pourrait produire un résultat légèrement différent ou inattendu.
Ces fragilités rendent les Transformers peu fiables dans des environnements critiques, comme la cybersécurité ou les applications médicales.
Problème n°5 : Le coût énergétique
Entraîner un Transformer comme GPT-4 consomme une quantité astronomique d’énergie. On estime que les émissions de carbone liées à l’entraînement d’un grand modèle de langage sont équivalentes à plusieurs centaines de vols transatlantiques. Cela pose un problème écologique majeur.
Alors, pourquoi la peur de l’apocalypse IA ?
Malgré leurs limitations, les Transformers suscitent des craintes, souvent exagérées, parce qu’ils :
- Imitent très bien l’intelligence humaine.
- Peuvent être utilisés à des fins malveillantes (désinformation, manipulation d’opinion, etc.).
- Évoluent rapidement, laissant penser que leurs limites actuelles pourraient bientôt disparaître.
Ce qu’il reste à améliorer
Pour dépasser leurs limites, les chercheurs explorent plusieurs pistes :
- Étendre la mémoire : En utilisant des architectures comme les Transformers récursifs ou des méthodes hybrides combinant mémoire à long terme et blocs standard.
- Réduire les biais : En intégrant des techniques d’entraînement éthiques et en filtrant les données problématiques.
- Optimiser l’énergie : Développer des modèles plus petits, mais plus efficaces, grâce à des méthodes comme les mixtes d’experts (MoE).
En conclusion
Les Transformers sont puissants, mais pas invincibles. Ils excellent dans des tâches bien définies, mais échouent dès qu’on leur demande de sortir des sentiers battus. Tant qu’ils dépendront des données imparfaites et resteront sensibles aux perturbations, ils seront plus des assistants brillants que des maîtres du monde.
Chapitre 11 : RAGs à gogo : Chercher des documents, c’est le vrai superpouvoir

Les Transformers sont souvent acclamés pour leur capacité à générer du texte, mais leur véritable potentiel se révèle lorsqu’ils s’attaquent à un problème très concret : retrouver de l’information. C’est ici que les RAGs (Retrieval-Augmented Generation) entrent en jeu. Imaginez-les comme des bibliothécaires surpuissants, capables de fouiller dans une montagne de documents pour trouver la réponse exacte à une question. Leur superpouvoir ? Mélanger recherche et génération.
RAG : De quoi s’agit-il ?
Un système RAG combine deux éléments :
- La recherche d’information (retrieval) : Extraire les passages pertinents d’une base de données ou d’une collection de documents.
- La génération de texte (generation) : Reformuler ces informations sous une forme compréhensible pour l’utilisateur.
C’est un peu comme si vous posiez une question à un Transformer, mais qu’il consultait une encyclopédie pour vous répondre au lieu de s’appuyer uniquement sur sa mémoire interne.
Comment fonctionne un système RAG ?
Le processus peut être résumé en trois étapes :
- Indexer les documents : Tous les documents disponibles sont convertis en représentations vectorielles à l’aide d’un modèle de langage pré-entraîné. Chaque document (ou fragment de document) est transformé en un vecteur
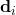 , stocké dans une base de données vectorielle.
, stocké dans une base de données vectorielle. - Effectuer une recherche vectorielle : Lorsque l’utilisateur pose une question, elle est également convertie en un vecteur
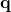 . Ensuite, on calcule la similarité entre ce vecteur et tous les vecteurs des documents :
. Ensuite, on calcule la similarité entre ce vecteur et tous les vecteurs des documents :
![]()
où ![]() désigne le cosinus de l’angle entre les deux vecteurs. Les documents les plus proches (avec le score le plus élevé) sont récupérés.
désigne le cosinus de l’angle entre les deux vecteurs. Les documents les plus proches (avec le score le plus élevé) sont récupérés.
Générer une réponse : Les passages extraits sont utilisés comme contexte pour le Transformer, qui génère une réponse en combinant ces informations avec sa propre connaissance.
Pourquoi RAG est-il révolutionnaire ?
Contrairement aux Transformers classiques, qui s’appuient uniquement sur leur modèle interne, les RAGs peuvent accéder à des informations actualisées et spécifiques. Cela présente plusieurs avantages :
- Réponses précises et contextuelles : Si une base de données contient les bonnes informations, le système peut fournir des réponses très précises.
- Mémoire illimitée : Pas besoin d’entraîner un modèle gigantesque pour mémoriser chaque fait ; les RAGs peuvent puiser dans des bases de données externes.
- Mise à jour facile : Mettre à jour les informations d’un RAG est aussi simple que d’ajouter ou de modifier des documents dans la base.
Un exemple concret :
Supposons que vous posiez une question à un système RAG :
« Quelle est la distance entre la Terre et la Lune ? »
Voici ce qu’il fait :
- Recherche dans une base de données contenant des informations astronomiques.
- Identifie un passage pertinent : « La distance moyenne entre la Terre et la Lune est de 384 400 km. »
- Génère une réponse fluide : « La distance moyenne entre la Terre et la Lune est d’environ 384 400 km. »
Les limites des RAGs
Bien que puissants, les RAGs ont leurs faiblesses :
- Qualité des données : Si la base contient des informations erronées, le système peut propager des erreurs.
- Temps de recherche : La recherche vectorielle peut être lente si la base est très grande.
- Complexité des requêtes : Pour des questions ambiguës ou mal formulées, le système peut récupérer des documents non pertinents.
Et dans le futur ?
Les RAGs pourraient devenir des outils essentiels dans :
- Les entreprises : Pour rechercher rapidement des informations dans des bases internes.
- La médecine : Pour accéder à des articles scientifiques ou des bases de données médicales.
- L’éducation : Pour aider les étudiants à trouver des réponses précises à des questions complexes.
En résumé
Les RAGs montrent que la vraie puissance des Transformers réside autant dans leur capacité à récupérer de l’information que dans leur aptitude à la générer. Avec des bases de données bien conçues, ils deviennent des assistants d’une précision redoutable. Mais comme tout bon assistant, ils dépendent fortement de la qualité des outils qu’ils utilisent.
Chapitre 12 : Transformer ton monde ou ton entreprise ? Prudence est mère de sûreté

L’utilisation des Transformers s’étend bien au-delà de la recherche académique. Aujourd’hui, les entreprises, les gouvernements et même les petites startups envisagent de les intégrer dans leurs opérations. Mais avant de plonger tête baissée, il est essentiel de comprendre les opportunités et les risques que cela implique.
Pourquoi les entreprises s’intéressent-elles aux Transformers ?
Les Transformers offrent des capacités impressionnantes qui peuvent transformer les processus d’entreprise :
- Automatisation : Répondre aux questions des clients via des chatbots, automatiser des rapports ou analyser des données massives.
- Personnalisation : Offrir des recommandations produits ou des publicités ultra-ciblées.
- Recherche avancée : Fouiller dans des bases de données complexes avec des outils comme les RAGs.
Un exemple concret : Le support client
Un Transformer peut être utilisé pour automatiser les réponses aux questions fréquentes d’un client. Supposons qu’un utilisateur demande :
« Comment changer mon mot de passe ? »
Le Transformer, entraîné sur des documents internes, pourrait générer une réponse détaillée :
« Pour changer votre mot de passe, allez dans les paramètres de votre compte, cliquez sur ‘Sécurité’, puis suivez les instructions. »
Cela peut réduire les coûts et améliorer la satisfaction client… à condition que le système soit bien configuré.
Les limites pratiques des Transformers en entreprise
Bien que séduisants, les Transformers ne sont pas une solution miracle. Voici quelques défis :
- Coût d’entraînement et d’infrastructure : Entraîner et déployer un modèle comme GPT-4 nécessite des ressources massives, ce qui peut être hors de portée pour de nombreuses entreprises.
- Sécurité des données : Les Transformers doivent souvent être connectés à des bases de données sensibles. Une mauvaise configuration peut entraîner des fuites de données.
- Fiabilité : Les réponses générées par un Transformer peuvent être incohérentes ou incorrectes, ce qui peut poser problème dans des contextes critiques.
Le piège des solutions « prêtes à l’emploi »
Certaines entreprises utilisent des services comme ChatGPT directement depuis le cloud. Bien que pratique, cela pose plusieurs questions :
- Confidentialité : Envoyer des données internes à un service tiers peut exposer des informations sensibles.
- Dépendance : Si le service tiers subit une panne ou décide d’augmenter ses prix, l’entreprise se retrouve bloquée.
La prudence est de mise : vers des solutions locales
Pour minimiser les risques, de plus en plus d’entreprises adoptent des solutions « on-premise », où le modèle est hébergé localement, sans connexion à Internet. Cela offre plusieurs avantages :
- Contrôle total sur les données.
- Réduction des risques de fuites.
- Adaptation spécifique aux besoins de l’entreprise.
Cependant, héberger un Transformer localement nécessite des compétences techniques et des infrastructures adaptées, ce qui n’est pas accessible à toutes les organisations.
Un équilibre entre ambition et précaution
Les Transformers sont des outils extraordinaires, mais ils nécessitent une planification soigneuse pour éviter les mauvaises surprises. Voici quelques conseils pour les entreprises :
- Commencer petit : Tester les modèles sur des cas d’usage simples avant d’envisager un déploiement massif.
- S’assurer de la qualité des données : Les données d’entraînement doivent être pertinentes et sans biais.
- Mettre en place des garde-fous : Ajouter des validations humaines pour éviter des réponses critiques incorrectes.
En conclusion
Les Transformers peuvent transformer le fonctionnement des entreprises, mais ils ne doivent pas être adoptés aveuglément. Avec une intégration réfléchie, ils peuvent devenir des outils précieux. Sans cela, ils risquent de devenir des sources de frustration… ou pire.
Chapitre 13 : Les maths derrière le buzz : Ce qu’on comprend vraiment (et ce qu’on ignore encore)

Les Transformers fascinent par leur efficacité et leur polyvalence. Mais au-delà de l’engouement médiatique, que comprenons-nous vraiment de leur fonctionnement ? Si les mathématiques sont au cœur de ces modèles, elles laissent aussi des zones d’ombre. Décryptons ce qui relève de la maîtrise, du mystère et du buzz.
Ce que l’on comprend : une belle mécanique mathématique
Les mathématiques derrière les Transformers sont solides, ce qui explique en grande partie leur succès. Voici les aspects que nous maîtrisons bien :
- Les vecteurs et matrices : des représentations puissantes Les mots, images ou sons sont traduits en vecteurs dans des espaces de grande dimension. Cela permet :
- De manipuler facilement des données complexes.
- D’appliquer des opérations linéaires et des transformations non linéaires efficaces.
- L’attention multi-tête : un super-pouvoir calculé Le mécanisme d’attention capte les relations entre tokens en attribuant des scores à chaque paire. Ce processus est bien compris mathématiquement :
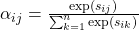
- Avec
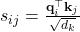 , les scores mesurent la pertinence entre tokens.
, les scores mesurent la pertinence entre tokens.
- L’optimisation par descente de gradient Les Transformers sont entraînés en minimisant une fonction de perte, comme l’entropie croisée, pour ajuster leurs milliards de paramètres. La descente de gradient stochastique est une méthode robuste et bien étudiée.
- La gestion des problèmes numériques Des techniques comme la normalisation des vecteurs ou la limitation des valeurs extrêmes (exponentielles stabilisées) permettent de garantir des calculs précis même dans des architectures profondes.
Ce qui reste mystérieux : les boîtes noires et les biais
Malgré ces bases solides, de nombreuses questions restent sans réponse :
- Pourquoi ça marche si bien ? Les Transformers produisent des résultats étonnamment bons dans des domaines variés. Mais pourquoi exactement leur architecture est-elle si efficace ? Par exemple :
- Pourquoi l’attention multi-tête capte-t-elle si bien le contexte sémantique ?
- Pourquoi certaines couches semblent apprendre des concepts abstraits, comme la grammaire ou la logique, sans supervision explicite ?
- Les biais du modèle Les Transformers reproduisent et amplifient parfois les biais présents dans leurs données d’entraînement. Cela soulève des questions éthiques :
- Peut-on garantir que les réponses générées sont justes ou impartiales ?
- Comment éviter que le modèle génère des contenus nuisibles ou discriminatoires ?
- Les limites de l’interprétabilité Avec des milliards de paramètres, il est difficile de savoir pourquoi le modèle choisit tel ou tel mot. On parle alors de boîte noire : le modèle fonctionne, mais ses décisions internes restent largement incompréhensibles.
- La généralisation et la créativité Les Transformers sont-ils vraiment capables de « raisonner » ou simplement de combiner des patterns appris ? Leur capacité à produire des réponses convaincantes reste essentiellement statistique.
Le rôle du buzz : entre fascination et désinformation
La popularité des Transformers repose autant sur leurs performances que sur le battage médiatique qui les entoure. Cependant, il est important de :
- Ne pas les surestimer : Les Transformers ne sont pas des intelligences conscientes capables de réflexion ou d’intentionnalité.
- Reconnaître leurs limites : Ils peuvent échouer dans des tâches nécessitant une compréhension profonde ou une logique rigoureuse.
Ce que cela signifie pour l’avenir
Les Transformers ne sont pas une fin en soi, mais une étape importante dans l’évolution des modèles d’apprentissage automatique. Voici les pistes prometteuses pour les années à venir :
- Des modèles plus explicables : Mieux comprendre comment les Transformers prennent leurs décisions est crucial pour leur fiabilité.
- Des solutions énergétiquement efficaces : Réduire leur empreinte carbone sera une priorité.
- Des applications éthiques et contrôlées : Garantir que les Transformers servent les intérêts de la société, et non l’inverse.
En conclusion : entre mathématiques et magie
Les Transformers incarnent une fusion fascinante entre mathématiques avancées et applications pratiques. Leur succès montre à quel point les bonnes idées mathématiques, bien mises en œuvre, peuvent avoir un impact énorme. Mais la fascination qu’ils suscitent ne doit pas masquer leurs limites : les Transformers sont des outils incroyables, mais loin d’être parfaits ou omnipotents.
Conclusion : Les Transformers, un équilibre entre puissance et limites

Les Transformers représentent une avancée spectaculaire dans le domaine de l’intelligence artificielle. Leur capacité à comprendre et générer du texte, à analyser des images, et même à fusionner plusieurs types de données en fait des outils d’une polyvalence incroyable. Pourtant, malgré leur succès, ils ne sont ni magiques ni sans faille.
En explorant leur fonctionnement, nous avons vu qu’ils reposent sur des bases mathématiques solides mais restent des boîtes noires sur bien des aspects. Leurs performances dépendent d’un mélange subtil de calculs optimisés, d’astuces algorithmiques et de masses gigantesques de données. Ils sont brillants dans des tâches bien définies, mais souvent limités lorsqu’il s’agit de compréhension profonde, de raisonnement abstrait ou de fiabilité absolue.
Alors, que faut-il retenir ? Les Transformers sont des outils puissants, mais ils doivent être utilisés avec discernement. Ils sont parfaits pour automatiser des tâches, explorer des idées ou chercher des informations. Mais lorsqu’il s’agit de décisions critiques ou d’applications sensibles, il est essentiel de garder un humain dans la boucle et de reconnaître leurs limites.
En fin de compte, les Transformers ne sont pas là pour remplacer l’intelligence humaine, mais pour la compléter. Avec un usage réfléchi, ils peuvent devenir des alliés précieux, capables d’ouvrir de nouvelles perspectives, tout en nous rappelant que les outils les plus sophistiqués restent des créations humaines – et qu’il est de notre responsabilité de les utiliser à bon escient.
Merci d’avoir voyagé dans cet univers complexe et fascinant. Maintenant, à vous de transformer vos connaissances en action !
 Pourton.info
Pourton.info 



