1 + 1 = 2 : La plus grande des vérités simples (ou comment les mathématiciens ont transpiré pour prouver l’évidence)

Chapitre 1 : Pourquoi 1 + 1 ne devrait pas être si facile

Ou pourquoi les mathématiciens adorent rendre la vie compliquée…

On pourrait croire que est une évidence mathématique, une vérité qui n’a même pas besoin d’être prouvée. Après tout, même un enfant peut comprendre qu’ajouter un caillou à un autre donne deux cailloux, n’est-ce pas ? Mais dans le monde fascinant des mathématiciens, les choses ne sont jamais aussi simples qu’elles en ont l’air. En fait, la « simple » addition est le résultat d’une structure sous-jacente beaucoup plus complexe qu’il n’y paraît.

Imaginez que les mathématiques sont un château de cartes. Si vous voulez que votre château tienne debout, vous devez poser des bases extrêmement solides. La simple addition de deux nombres naturels est en fait une pierre angulaire de ce château. Si cette base n’est pas rigoureusement prouvée, tout l’édifice mathématique pourrait s’effondrer. Voilà pourquoi les mathématiciens ont pris la peine de formuler une preuve rigoureuse de cette opération.

Ce qui est amusant, c’est qu’il ne suffit pas de dire « tout le monde sait que « , comme on pourrait le faire dans une conversation ordinaire. En mathématiques, il faut partir des axiomes — des vérités fondamentales que l’on admet sans preuve — et construire tout le reste à partir de là. Si on ne prouve pas rigoureusement des choses aussi basiques, comment pourrait-on prouver quoi que ce soit de plus complexe ?

La beauté de tout cela réside dans la rigueur et l’amour du détail. Si vous avez déjà eu l’impression que les mathématiciens aiment « se prendre la tête » pour rien, ce chapitre vous montrera que parfois, cette obsession du détail est essentielle pour garantir que le reste des mathématiques est parfaitement cohérent.

Alors, attachez vos ceintures, car la démonstration que est bien plus une aventure qu’une simple addition !

Chapitre 2 : La longue route vers la rigueur : de Peano à Russell et Whitehead

Ou pourquoi prouver l’évidence prend environ 379 pages…

L’histoire de la démonstration de ne commence pas avec une simple feuille de papier, mais avec des axiomes profonds qui forment les bases des nombres naturels. Pour ceux qui ne le savent pas encore, un axiome est une déclaration que l’on accepte comme vraie sans preuve, mais qui nous permet de démontrer d’autres propositions. Et lorsqu’il s’agit de manipuler des nombres comme et , on doit commencer par définir ces nombres de façon rigoureuse.

L’un des systèmes axiomatiques les plus utilisés pour définir les nombres naturels est celui développé par Giuseppe Peano à la fin du 19e siècle. Peano a défini les nombres naturels à l’aide de cinq axiomes, connus sous le nom d’axiomes de Peano. Voici un aperçu rapide de ces axiomes :

1. Axiome 1 : 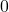est un nombre naturel.
2. Axiome 2 : Pour chaque nombre naturel 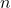, il existe un successeur 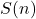qui est aussi un nombre naturel.
3. Axiome 3 : 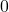n’est le successeur d’aucun nombre naturel.
4. Axiome 4 : Si deux nombres naturels ont le même successeur, alors ces deux nombres sont égaux.
5. Axiome 5 (Principe d’induction) : Si 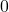a une propriété, et si, chaque fois qu’un nombre naturel 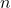a cette propriété, son successeur 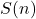l’a aussi, alors tous les nombres naturels ont cette propriété.

Cela semble simple, non ? Eh bien, pas si vite ! Même si ces axiomes sont très fondamentaux, ils ne suffisent pas à eux seuls à prouver que . Il faut aussi définir ce que signifie « additionner » deux nombres naturels et établir que l’opération fonctionne comme on le pense intuitivement.

Et c’est là qu’interviennent Bertrand Russell et Alfred North Whitehead avec leur œuvre monumentale Principia Mathematica, publiée en trois volumes entre 1910 et 1913. Leur mission ? Fonder toute la logique mathématique sur une base rigoureuse. Ils ont passé des centaines de pages à établir les bases les plus fondamentales des mathématiques, y compris la démonstration que .

Russell et Whitehead ont utilisé les axiomes de Peano pour définir les nombres et l’opération d’addition. Mais, pour montrer que , ils ont dû faire appel à toute une panoplie de résultats intermédiaires, tels que la définition du nombre comme le successeur de (c’est-à-dire ) et l’addition de deux nombres naturels en utilisant le concept de successeur.

Ainsi, après de longues pages d’abstraction, ils ont finalement démontré que . Ce résultat, aussi simple soit-il, représente le sommet d’une montagne de concepts logiques qui permettent de justifier l’addition des nombres naturels.

Chapitre 3 : Les axiomes de Peano : Quand les bases deviennent casse-tête

Un simple 1 devient un cauchemar…

Avant de se plonger dans la démonstration formelle que , il est crucial de comprendre pourquoi les axiomes de Peano sont si importants. À première vue, les axiomes semblent juste poser des règles simples pour décrire les nombres naturels et leur succession. Mais en réalité, chaque axiome est une pierre angulaire qui garantit que toute la structure mathématique qui en découle est cohérente.

Commençons par le premier axiome : est un nombre naturel. Cela semble basique, mais dans l’univers formel des mathématiques, il faut commencer quelque part. Ensuite, l’axiome suivant introduit le successeur : pour tout nombre , il existe un successeur , c’est-à-dire le nombre qui vient juste après . Si vous avez , son successeur est , que l’on appelle .

Le concept de « successeur » est fondamental parce qu’il permet de définir l’ensemble des nombres naturels sans avoir besoin de les énumérer explicitement. Vous commencez par , et ensuite, vous pouvez obtenir tous les autres nombres en répétant simplement l’opération du successeur : , , , et ainsi de suite.

Mais ce n’est pas tout : l’axiome 3 est là pour assurer que n’est le successeur d’aucun autre nombre. En d’autres termes, il n’existe pas de nombre naturel tel que . Cette règle peut sembler triviale, mais elle empêche que l’on « boucle » sur , garantissant ainsi que la suite des nombres naturels ne revient jamais en arrière.

Enfin, il y a le fameux principe d’induction (axiome 5). Il s’agit d’un des outils les plus puissants des mathématiques. L’idée derrière l’induction est que, si vous pouvez prouver qu’une propriété est vraie pour , et qu’elle est aussi vraie pour le successeur de n’importe quel nombre naturel pour lequel elle est vraie, alors vous pouvez conclure que cette propriété est vraie pour tous les nombres naturels.

Avec tout cela en place, nous avons un cadre robuste pour travailler avec les nombres naturels. Mais la route vers ne s’arrête pas là. Il faut encore définir comment fonctionne l’addition dans ce cadre formel.

En mathématiques, même une opération aussi simple que l’addition nécessite une définition rigoureuse. En utilisant les axiomes de Peano, on définit l’addition de deux nombres naturels de la manière suivante :

• Pour tout nombre naturel 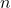, on définit .
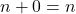• Pour tout nombre naturel 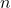et 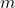, on définit .

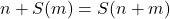En gros, cela signifie qu’ajouter à un nombre ne le change pas (ce qui est intuitif), et que pour ajouter un nombre à un successeur, on ajoute d’abord ce nombre au prédécesseur, puis on applique le successeur au résultat. Ce processus, en apparence simple, est la clé de la définition de l’addition dans un cadre formel rigoureux.

Donc, quand on dit , on peut voir que cette affirmation découle directement des axiomes de Peano et de la définition formelle de l’addition. Ce qui, au début, semblait une simple opération, est en fait soutenu par une architecture mathématique complexe et logique.

Chapitre 4 : L’épopée de Principia Mathematica : 1 + 1 = 2, mais en 1913

Spoiler : vous auriez déjà eu votre diplôme avant la fin de la preuve !

Si vous pensiez qu’une simple démonstration de allait tenir en deux ou trois lignes, préparez-vous à être surpris. Dans le monumental Principia Mathematica, écrit par Bertrand Russell et Alfred North Whitehead, il faut attendre la page 379 pour arriver à la démonstration tant attendue. Oui, vous avez bien lu : presque 400 pages de logique rigoureuse pour prouver ce que la plupart des enfants savent déjà en arrivant à l’école primaire.

Mais pourquoi diable tant de pages pour une vérité aussi évidente ? C’est là que réside toute la beauté (ou la folie, selon votre point de vue) de ce projet titanesque. Principia Mathematica n’était pas un simple manuel de mathématiques. C’était une tentative ambitieuse de fonder toutes les mathématiques sur la logique pure, sans faire appel à l’intuition ou à des « évidences » non prouvées.

Russell et Whitehead ont construit leur système logique à partir de zéro. Ils voulaient que chaque concept, chaque opération, soit dérivé de principes logiques fondamentaux. Pour eux, même des affirmations aussi simples que devaient être démontrées avec la plus grande rigueur. Ils ont commencé par poser les bases de la logique et de l’arithmétique, en utilisant des symboles et des notations qui rendent la lecture plutôt… austère.

Pour vous donner une idée de la démonstration formelle qu’ils ont développée, voici une version simplifiée (beaucoup plus digeste que dans le texte original) :

1. Ils définissent d’abord le nombre 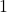comme le successeur de 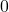, donc .
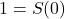2. Ils définissent ensuite le nombre 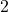comme le successeur de 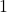, donc .
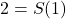3. L’addition est définie comme nous l’avons vu dans le chapitre précéden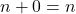t : , et .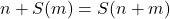

La démonstration complète que suit cette logique, avec des dizaines de résultats intermédiaires qui assurent que tout est absolument cohérent. Mais tout cela est emballé dans un langage si formel qu’il devient difficile de suivre sans avoir un doctorat en logique.

Voici comment cela se déroule, en version simplifiée :
Nous savons que et nous voulons prouver que . En appliquant la définition de l’addition, nous avons :

.

Mais nous savons que pour tout , donc :

.

Et voilà, nous obtenons bien que , c’est-à-dire . Facile, non ? Eh bien, peut-être pas aussi facile qu’on pourrait le penser au premier abord, mais c’est le fruit d’une rigueur extrême.

Russell et Whitehead ont prouvé qu’en partant des principes les plus fondamentaux, même une affirmation aussi simple que nécessite une démonstration. Ce projet de formalisation des mathématiques a eu un impact énorme sur la manière dont les mathématiciens abordent les fondements de leur discipline, bien que peu de gens, à part les plus intrépides, aient pris le temps de lire les 379 premières pages.

Chapitre 5 : La rigueur logique : Est-ce que 1 et 1, c’est vraiment pareil ?

Quand additionner devient une question existentielle.

À ce stade, vous vous dites peut-être : « OK, je comprends que la démonstration de nécessite une base rigoureuse, mais pourquoi compliquer les choses autant ? Après tout, c’est , non ? » Eh bien, pas si vite ! En mathématiques, même cette affirmation simple doit être examinée avec soin.

Revenons un peu en arrière. Quand nous disons que , que signifie réellement le symbole ? Si vous vous arrêtez pour réfléchir un instant, pourrait représenter n’importe quoi : un caillou, un mouton, une planète, ou même un sandwich (ne jamais sous-estimer l’importance des sandwichs). Mais comment savons-nous que tous ces « uns » sont les mêmes ? Et quand nous les additionnons, pourquoi pouvons-nous supposer qu’ils se comportent de manière identique ?

C’est là qu’intervient la notion de rigueur logique. En mathématiques, quand nous parlons de , il ne s’agit pas simplement de compter des objets concrets. est une abstraction qui représente une unité élémentaire, sans spécifier à quoi elle se rapporte. Et cette abstraction doit obéir à certaines règles pour que les opérations comme l’addition aient un sens cohérent.

L’une des grandes questions qui se pose alors est : comment être sûr que ces « uns » que nous additionnons sont véritablement les mêmes ? Si nous avons un « un » qui représente un mouton et un autre « un » qui représente un sandwich, est-ce vraiment pertinent de les additionner ? Bien sûr, dans notre quotidien, on peut ignorer ces distinctions, mais en mathématiques, chaque détail compte.

Prenons un exemple concret : imaginez que nous travaillons avec des ensembles, et que nous définissons le nombre comme l’ensemble qui ne contient qu’un seul élément, par exemple

. L’opération consisterait alors à unir deux ensembles contenant chacun un élément, donc

. Si nous savons que les éléments sont distincts, cela fait bien . Mais si les éléments étaient en fait identiques (comme deux moutons blancs indistinguables), alors cette union ne changerait rien : nous n’obtiendrions toujours qu’un seul mouton !

Voilà pourquoi il est si important de définir clairement ce que nous entendons par dans un cadre mathématique. Quand nous disons que , nous faisons abstraction des spécificités des objets individuels et nous traitons les unités de manière complètement formelle. C’est grâce à cette abstraction que nous pouvons affirmer avec certitude que , peu importe ce que « un » représente.

Cette rigueur est ce qui garantit que les mathématiques fonctionnent dans des contextes aussi divers que la comptabilité, la physique, ou encore la théorie des nombres. Sans cette rigueur, nous pourrions rapidement tomber dans des contradictions ou des paradoxes. Imaginez un monde où ne fait pas toujours … ce serait le chaos ! Heureusement, les mathématiciens ont tout prévu pour que ce genre de situation n’arrive jamais.

Chapitre 6 : Pourquoi on adore compliquer ce qui est simple : La philosophie des fondements

Bienvenue dans l’abîme du doute mathématique.

Les mathématiciens ont la réputation de compliquer les choses, même lorsque tout semble clair. Et la démonstration que en est un exemple frappant. Pourquoi prendre autant de temps pour prouver ce qui semble être une évidence ? La réponse réside dans la philosophie des mathématiques, une branche qui explore les fondements mêmes de cette discipline.

Vous pourriez penser que, dans un monde idéal, les mathématiques reposeraient sur des vérités évidentes et indiscutables. Mais l’histoire a montré que ce n’est pas toujours aussi simple. Le doute philosophique a mené à des révolutions majeures en mathématiques, notamment à la fin du 19e et au début du 20e siècle. À cette époque, les mathématiciens ont réalisé que leur discipline, qui semblait si stable et solide, reposait sur des fondements beaucoup plus fragiles qu’ils ne l’imaginaient.

Un des moments clés de cette réflexion a été la découverte de paradoxes dans la théorie des ensembles, comme le célèbre paradoxe de Russell. Si vous vous souvenez, Russell est le même qui, avec Whitehead, a écrit Principia Mathematica, où il a prouvé que . Avant cela, il a découvert que certaines constructions mathématiques, que l’on pensait intuitives, menaient à des contradictions logiques.

L’un de ces paradoxes est le suivant : supposons que nous définissions l’ensemble comme l’ensemble de tous les ensembles qui ne se contiennent pas eux-mêmes. La question est alors : est-ce que se contient lui-même ? Si se contient, alors par définition, il ne devrait pas se contenir. Mais s’il ne se contient pas, alors selon la définition, il doit se contenir. Ce paradoxe a mis en évidence une faille dans la manière dont les mathématiciens pensaient aux ensembles et aux nombres.

C’est en réponse à de tels paradoxes que des mathématiciens comme Russell et Whitehead ont entrepris de formaliser rigoureusement toutes les mathématiques à partir de la logique. Ils voulaient s’assurer que les bases de leur discipline étaient solides, pour éviter tout risque de contradiction. C’est cette quête de certitude qui les a menés à prouver que , en partant des principes les plus fondamentaux.

Cette rigueur est essentielle pour assurer que tout l’édifice mathématique tient la route. Car si l’on ne peut pas prouver une simple addition, comment pourrait-on avoir confiance dans des théories plus complexes comme celles de l’analyse ou de l’algèbre ? En poussant l’exigence de rigueur à l’extrême, les mathématiciens ont créé une discipline qui, malgré ses fondements abstraits, est capable de modéliser le monde réel avec une précision impressionnante.

Alors oui, il peut sembler exagéré de passer des centaines de pages à prouver que , mais cette démarche s’inscrit dans une quête plus large : celle de comprendre les bases mêmes de notre compréhension du monde. Et dans cette quête, chaque détail compte, aussi petit soit-il.

Chapitre 7 : 1 + 1 = 2 : Plus fondamental que la gravité ?

Vous croyez que c’est une blague, mais attendez la fin…

La démonstration que semble être une simple formalité, mais en réalité, elle touche à quelque chose d’encore plus fondamental dans notre compréhension du monde. En fait, on pourrait dire que cette équation est plus stable que certaines des lois physiques que nous utilisons pour décrire l’univers !

Prenons un exemple : la gravité. Nous vivons dans un monde où nous sommes familiers avec les lois de la gravité. L’attraction gravitationnelle nous retient sur Terre, et les objets tombent lorsqu’ils sont lâchés. Mais la gravité, telle que nous la connaissons, repose sur des théories, comme celle de la relativité générale d’Einstein, qui, bien que très robustes, sont susceptibles de changement ou de raffinement à mesure que nous découvrons plus de choses sur l’univers.

Cependant, l’addition de ne dépend pas de théories physiques, ni de notre position dans l’espace ou le temps. Cette vérité est valable dans tous les contextes, que ce soit sur Terre, dans une autre galaxie, ou même dans un univers parallèle où les lois de la physique seraient complètement différentes. Elle est absolue, universelle et intemporelle.

Pourquoi ? Parce que les mathématiques, contrairement à la physique, ne sont pas basées sur l’observation de l’univers, mais sur des concepts abstraits que nous définissons nous-mêmes. Lorsque nous prouvons que , nous établissons une vérité qui découle directement des axiomes que nous avons posés. Ces axiomes peuvent être choisis de manière à être applicables dans n’importe quel cadre logique, que ce soit dans notre monde ou dans un monde fictif.

En d’autres termes, si demain un extraterrestre débarquait sur Terre et nous disait que, sur sa planète, , nous pourrions lui répondre avec confiance : « Non, vous devez avoir mal compris vos axiomes de base. » Peu importe la physique ou les circonstances, cette vérité restera la même.

Cela montre à quel point les mathématiques sont un langage universel, capable de transcender les lois physiques que nous observons. Tandis que la gravité peut s’effondrer dans certaines situations extrêmes (comme à l’intérieur des trous noirs), ne faillit jamais. C’est une vérité mathématique qui, contrairement aux lois de la nature, n’est pas sujette à l’expérimentation ou à la falsification.

En conclusion, la démonstration de est bien plus qu’un simple exercice de rigueur mathématique. C’est une illustration de la beauté et de la robustesse des mathématiques, un rappel que même les vérités les plus élémentaires reposent sur des bases solides, et que sans elles, tout ce que nous construisons en mathématiques — et même en science — risquerait de s’effondrer.