Chapitre 1 : Introduction – Le Duel Éternel
Si je vous demandais de citer deux concepts mathématiques opposés, il y a de fortes chances que vous pensiez immédiatement à l’addition et la soustraction ou à la multiplication et la division. Mais que diriez-vous des dérivées et des intégrales ? Bien que ces notions puissent sembler complexes et parfois même infiniment complexes, elles sont au cœur de l’analyse mathématique et jouent un rôle crucial dans de nombreux domaines de la science.
Laissez-moi vous présenter ce duel éternel : la dérivée, qui nous parle de la pente et de la variation instantanée, et l’intégrale, qui nous permet de mesurer l’aire sous une courbe. Deux concepts apparemment opposés mais intimement liés.
Pourquoi les dérivées et les intégrales sont-elles si fascinantes ?
Les mathématiques sont souvent perçues comme un ensemble de règles rigides et d’équations inaccessibles. Cependant, elles sont aussi un langage universel qui décrit le monde qui nous entoure. Les dérivées et les intégrales sont des outils puissants pour explorer et comprendre ce monde. La dérivée nous donne la vitesse à laquelle une quantité change, tandis que l’intégrale nous permet de cumuler ces changements pour obtenir une mesure totale.
Les fondements de l’opposition mathématique
Prenons un exemple simple. Imaginez que vous conduisiez une voiture sur une autoroute. La dérivée de votre position par rapport au temps, que nous appellerons ![]() , est votre vitesse, notée
, est votre vitesse, notée ![]() . Si vous connaissez votre vitesse à tout moment, l’intégrale de cette vitesse sur un intervalle de temps vous donnera la distance totale parcourue :
. Si vous connaissez votre vitesse à tout moment, l’intégrale de cette vitesse sur un intervalle de temps vous donnera la distance totale parcourue : ![]() .
.
En d’autres termes, la dérivée nous dit comment quelque chose change à un instant donné, tandis que l’intégrale cumule ces changements pour nous donner une mesure globale.
Le Langage Mathématique
Pour naviguer dans cet article, il est important de se familiariser avec quelques notations mathématiques essentielles :
- La dérivée d’une fonction
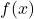 est notée
est notée 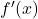 ou
ou 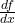 .
. - L’intégrale d’une fonction
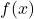 sur un intervalle
sur un intervalle ![Rendered by QuickLaTeX.com [a, b]](https://pourton.info/wp-content/ql-cache/quicklatex.com-f4ba939765d40e92df3eb5d5baa2da4e_l3.png) est notée
est notée 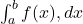 .
. - La primitive ou l’antidérivée de
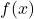 , qui est une fonction
, qui est une fonction 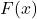 telle que
telle que 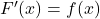 , est notée
, est notée 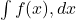 .
.
La suite …
Accrochez-vous, car nous allons plonger dans les profondeurs de ces deux concepts fascinants, tout en gardant un ton léger et une bonne dose d’humour ! Préparez-vous à explorer les mystères des dérivées et des intégrales, et à découvrir comment ces outils mathématiques peuvent éclairer notre compréhension du monde.
Chapitre 2 : Newton et l’Invention du Calcul Infinitésimal
Un petit tour dans le passé : Newton, le père des dérivées
Isaac Newton, souvent associé à la célèbre pomme et à la loi de la gravitation universelle, est également une figure centrale dans le développement du calcul infinitésimal. Ses travaux en physique et en mathématiques ont révolutionné notre compréhension du monde.
Au XVIIe siècle, Newton a posé les bases de ce que nous appelons aujourd’hui le calcul différentiel et intégral. Ce fut une époque où les mathématiques connurent une expansion rapide, et Newton, avec son rival Leibniz, joua un rôle clé dans cette évolution.
Comment Newton a-t-il révolutionné les mathématiques ?
Newton a introduit le concept de la dérivée comme une manière de décrire le changement instantané. Plutôt que de se contenter de la vitesse moyenne sur un intervalle de temps, il voulait savoir comment une quantité changeait à un moment précis. Cette idée a conduit à la notion de la dérivée.
Imaginons que vous observiez la trajectoire d’une comète dans le ciel. La position de la comète à un moment donné peut être représentée par une fonction ![]() , où
, où ![]() est le temps. La dérivée de cette fonction, notée
est le temps. La dérivée de cette fonction, notée ![]() ou
ou ![]() , nous donne la vitesse instantanée de la comète.
, nous donne la vitesse instantanée de la comète.
Newton a formulé cela mathématiquement en définissant la dérivée comme :
![]()
Cette formule capture l’idée du taux de changement instantané.
Les premiers pas du calcul infinitésimal
Le calcul infinitésimal de Newton ne s’arrêtait pas aux dérivées. Il a également travaillé sur les intégrales, qu’il voyait comme le processus inverse de la différentiation. Par exemple, si nous connaissons la vitesse ![]() d’un objet à tout instant, nous pouvons retrouver sa position en intégrant la vitesse sur le temps :
d’un objet à tout instant, nous pouvons retrouver sa position en intégrant la vitesse sur le temps :
![]()
Newton a ainsi posé les bases de ce que l’on appelle aujourd’hui le théorème fondamental de l’analyse, qui lie la dérivée et l’intégrale de manière profonde et élégante.
Le Génie de Newton
Ce qui rend les contributions de Newton si remarquables, c’est qu’il a développé ces concepts non seulement pour résoudre des problèmes théoriques, mais aussi pour aborder des questions pratiques en physique. Ses méthodes ont permis des avancées majeures, telles que la description précise des mouvements des planètes et des objets sur Terre.
Un génie inspirant
Isaac Newton n’était pas seulement un génie des mathématiques et de la physique. Il était aussi quelqu’un qui savait voir au-delà de l’évidence pour découvrir des vérités fondamentales. En inventant le calcul infinitésimal, il a ouvert la voie à des générations de scientifiques et de mathématiciens qui continuent d’explorer les mystères de notre univers.
Chapitre 3 : Les Dérivées : La Magie de la Pente
Qu’est-ce qu’une dérivée et pourquoi c’est important ?
Une dérivée, c’est un outil mathématique qui permet de mesurer le taux de changement instantané d’une fonction. En d’autres termes, elle nous indique à quelle vitesse une quantité varie par rapport à une autre. C’est un concept essentiel en mathématiques et en physique, car il permet de comprendre comment les choses évoluent au fil du temps.
Imaginons que vous grimpiez une montagne. La pente à chaque instant de votre ascension peut être représentée par la dérivée de la fonction qui décrit votre altitude par rapport à la distance parcourue. Si l’altitude est donnée par une fonction ![]() , alors la dérivée
, alors la dérivée ![]() nous donne la pente de la montagne à chaque point.
nous donne la pente de la montagne à chaque point.
La méthode de Newton pour comprendre les courbes
Newton a révolutionné notre compréhension des courbes en introduisant la notion de dérivée. Pour une fonction ![]() , la dérivée est définie comme :
, la dérivée est définie comme :
![]()
Cette définition mathématique capture l’idée de la pente instantanée d’une courbe en un point. En simplifiant, on peut dire que la dérivée mesure la « steepness » de la courbe à ce point.
Exemples concrets : De la montagne russe à la physique quantique
Pour mieux comprendre les dérivées, examinons quelques exemples concrets :
- Montagne Russe : Imaginez un roller coaster. La dérivée de la position du wagon par rapport au temps donne la vitesse du wagon. La dérivée de la vitesse donne l’accélération, qui est ressentie comme les « G-forces » par les passagers.
- Économie : En économie, la dérivée du coût total par rapport à la quantité produite est appelée le coût marginal. Elle indique le coût supplémentaire pour produire une unité supplémentaire d’un bien.
- Physique Quantique : En physique quantique, les dérivées sont utilisées pour décrire des phénomènes comme la probabilité de trouver une particule dans une certaine région de l’espace. La célèbre équation de Schrödinger utilise des dérivées pour décrire l’évolution temporelle des systèmes quantiques.
La dérivée en action : un outil polyvalent
Les dérivées ne sont pas seulement utiles pour les mathématiciens et les physiciens. Elles sont omniprésentes dans notre vie quotidienne. Par exemple, lorsque vous utilisez un GPS pour naviguer, les dérivées sont utilisées pour calculer la vitesse et l’accélération de votre véhicule.
La pente des mystères
La dérivée, c’est un peu comme un détective privé des mathématiques. Elle nous dit ce qui se passe instantanément, en révélant les changements subtils et les variations soudaines. Grâce à Newton, nous avons un outil puissant pour explorer les pentes des montagnes, les courbes de l’économie et même les mystères de l’univers quantique.
Chapitre 4 : Les Intégrales : L’Art de Mesurer l’Incommensurable
Introduction à l’intégrale : de Riemann à aujourd’hui
Après Newton, un autre mathématicien de génie, Bernhard Riemann, a apporté une contribution fondamentale à notre compréhension des intégrales. Au XIXe siècle, Riemann a formalisé la notion d’intégrale, permettant de mesurer l’aire sous une courbe de manière rigoureuse. Ses travaux ont jeté les bases de l’analyse moderne.
L’intégrale est l’outil qui nous permet de cumuler des quantités infiniment petites pour obtenir une mesure totale. Si la dérivée nous dit comment une quantité change instantanément, l’intégrale nous permet de mesurer l’accumulation de ces changements sur un intervalle donné.
Calculer l’aire sous une courbe : Pourquoi et comment ?
Calculer l’aire sous une courbe est une question centrale en mathématiques. Cela revient à sommer une infinité de petites aires pour obtenir une aire totale. Si vous avez une fonction ![]() , l’intégrale de
, l’intégrale de ![]() sur l’intervalle
sur l’intervalle ![]() est notée :
est notée :
![]()
Cela représente l’aire sous la courbe de ![]() entre les points
entre les points ![]() et
et ![]() .
.
Riemann a proposé une méthode pour approximar cette aire en utilisant des sommes de Riemann, où l’aire est approximée par une somme de petits rectangles. Lorsque la largeur de ces rectangles tend vers zéro, la somme de Riemann devient l’intégrale définie.
Applications pratiques : Du réservoir d’essence aux galaxies lointaines
Les intégrales ont des applications pratiques dans de nombreux domaines :
- Réservoir d’essence : Pour déterminer la quantité d’essence consommée sur un trajet, on peut intégrer la consommation instantanée de carburant sur la durée du trajet.
- Électricité : En électromagnétisme, l’intégrale permet de calculer le flux électrique à travers une surface.
- Astronomie : Les astronomes utilisent des intégrales pour déterminer la masse totale d’une galaxie en intégrant la densité de matière sur son volume.
Le génie de Riemann
La méthode de Riemann a permis de formaliser et de généraliser le calcul des aires et des volumes dans des contextes complexes. Son approche a ouvert la voie à des développements ultérieurs en analyse, et les intégrales de Riemann restent un outil essentiel en mathématiques et en physique.
La beauté de l’accumulation
L’intégrale, c’est un peu comme un artiste peintre qui crée une œuvre en accumulant des touches de pinceau. Chaque petite touche contribue à l’ensemble, et ce n’est qu’en prenant du recul que l’on peut admirer la beauté de l’œuvre finale. Grâce à Riemann, nous avons un moyen de mesurer l’incommensurable, de l’énergie d’une particule à la masse d’une galaxie entière.
Chapitre 5 : Le Lien Étrange Entre Dérivées et Intégrales
Comment ces deux concepts sont-ils reliés ?
Les dérivées et les intégrales peuvent sembler être des concepts distincts, mais ils sont en réalité profondément liés par ce que l’on appelle le théorème fondamental de l’analyse. Ce théorème établit un pont entre la dérivation et l’intégration, montrant qu’elles sont, en quelque sorte, des opérations inverses l’une de l’autre.
Le théorème fondamental de l’analyse se compose de deux parties principales :
- Première Partie : Si
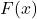 est une primitive de
est une primitive de 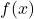 , c’est-à-dire que
, c’est-à-dire que 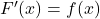 , alors l’intégrale définie de
, alors l’intégrale définie de 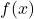 de
de  à
à 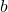 est donnée par :
est donnée par :
![]()
Deuxième Partie : Si ![]() est continue sur
est continue sur ![]() , alors la fonction
, alors la fonction ![]() définie par
définie par
![]()
est une primitive de ![]() .
.
Ces deux parties montrent que l’intégration peut être utilisée pour « annuler » la dérivation, et vice versa. En d’autres termes, dériver une intégrale nous ramène à la fonction originale, et intégrer une dérivée nous donne la variation totale de la fonction.
Les fondamentaux du théorème fondamental de l’analyse
Le théorème fondamental de l’analyse relie les concepts d’intégrale et de dérivée de manière élégante et puissante. Il nous dit que pour une fonction continue, l’intégrale de sa dérivée sur un intervalle nous donne le changement total de la fonction sur cet intervalle. Cela peut sembler abstrait, mais ce lien a des implications profondes et pratiques.
Des exemples pratiques pour mieux comprendre
Voyons quelques exemples concrets pour illustrer le théorème fondamental de l’analyse :
- Exemple 1 : Déplacement et Vitesse
Si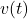 est la vitesse d’un objet à un instant
est la vitesse d’un objet à un instant 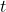 , alors le déplacement total de l’objet de
, alors le déplacement total de l’objet de 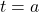 à
à 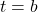 est donné par :
est donné par :
![]()
où ![]() est la position de l’objet à l’instant
est la position de l’objet à l’instant ![]() .
.
Exemple 2 : Coût et Taux de Production
Si ![]() représente le coût marginal de production (le coût pour produire une unité supplémentaire) d’un bien, alors le coût total pour produire de
représente le coût marginal de production (le coût pour produire une unité supplémentaire) d’un bien, alors le coût total pour produire de ![]() à
à ![]() unités est donné par :
unités est donné par :
![]()
Le pont entre deux mondes
Le théorème fondamental de l’analyse n’est pas seulement une curiosité mathématique. Il est le pont qui relie deux des concepts les plus importants des mathématiques : la dérivée et l’intégrale. Grâce à ce théorème, nous pouvons naviguer sans effort entre le monde des taux de changement instantanés et celui des accumulations totales, ouvrant ainsi des perspectives infinies dans notre compréhension de l’univers.
Chapitre 6 : Les Primitives : L’Inversion Magique
Qu’est-ce qu’une primitive et pourquoi est-elle essentielle ?
Une primitive, également appelée antiderivée, est une fonction qui, lorsqu’elle est dérivée, donne une fonction donnée. En d’autres termes, si vous avez une fonction ![]() , une primitive de
, une primitive de ![]() est une fonction
est une fonction ![]() telle que
telle que ![]() .
.
Les primitives sont essentielles car elles permettent de résoudre des problèmes d’intégration. Trouver la primitive d’une fonction est en fait l’opération inverse de la dérivation, ce qui en fait un outil crucial en analyse mathématique.
Les subtilités du +C : Pourquoi il ne faut jamais l’oublier
Lorsque vous trouvez une primitive d’une fonction, vous devez toujours ajouter une constante arbitraire ![]() . Cela vient du fait que la dérivée d’une constante est zéro. Par conséquent, si
. Cela vient du fait que la dérivée d’une constante est zéro. Par conséquent, si ![]() est une primitive de
est une primitive de ![]() , alors
, alors ![]() est aussi une primitive de
est aussi une primitive de ![]() .
.
Par exemple, si ![]() , une primitive de
, une primitive de ![]() est
est ![]() . Mais
. Mais ![]() ,
, ![]() , et
, et ![]() où
où ![]() est une constante, sont également des primitives de
est une constante, sont également des primitives de ![]() .
.
Exemples et applications : Quand les constantes font la différence
Voyons quelques exemples pour mieux comprendre l’importance des constantes dans les primitives :
- Exemple 1 : Calculer une primitive simple
Pour la fonction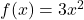 , une primitive est
, une primitive est 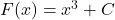 . Ici,
. Ici, 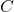 représente n’importe quelle constante réelle.
représente n’importe quelle constante réelle. - Exemple 2 : Problèmes pratiques
Si vous avez une fonction représentant une vitesse, comme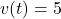 , cela signifie que l’objet se déplace à une vitesse constante de 5 unités par temps. La primitive de
, cela signifie que l’objet se déplace à une vitesse constante de 5 unités par temps. La primitive de 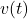 est
est 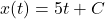 , où
, où 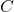 est la position initiale de l’objet. Sans cette constante, vous ne pourriez pas déterminer la position initiale de l’objet.
est la position initiale de l’objet. Sans cette constante, vous ne pourriez pas déterminer la position initiale de l’objet.
La magie de l’inversion
Les primitives ajoutent une dimension de flexibilité et de profondeur à notre compréhension des fonctions et des intégrales. En permettant de revenir en arrière de la dérivée à la fonction originale, elles complètent l’image du calcul infinitésimal. Avec le +C, elles nous rappellent que même dans les mathématiques les plus rigoureuses, il y a toujours une place pour l’inattendu et l’inconnu.
Chapitre 8 : Les Dérivées et Intégrales dans la Vie Quotidienne
Comment ces concepts mathématiques influencent notre quotidien ?
Les dérivées et les intégrales ne sont pas seulement des concepts théoriques réservés aux mathématiciens et aux physiciens. Ils jouent également un rôle essentiel dans notre vie quotidienne, souvent sans que nous nous en rendions compte. Que ce soit pour prévoir la météo, optimiser des trajets, ou encore analyser des données financières, ces outils mathématiques sont partout.
Des anecdotes amusantes sur les dérivées et les intégrales
Pour rendre ces concepts plus accessibles, explorons quelques anecdotes amusantes :
- Prévisions météorologiques : Les modèles météorologiques utilisent des équations différentielles pour prédire l’évolution des conditions météorologiques. Ces équations sont basées sur les dérivées des variables météorologiques telles que la température, la pression et la vitesse du vent. Sans les dérivées, prévoir la météo serait impossible.
- Navigation GPS : Les GPS utilisent des intégrales pour calculer les trajets les plus courts et les plus rapides. En intégrant la vitesse de votre véhicule sur le temps, ils peuvent déterminer la distance parcourue et ajuster votre itinéraire en temps réel.
- Economie et finances : Les dérivées sont utilisées pour analyser les tendances du marché et pour optimiser les stratégies de trading. Par exemple, la dérivée du prix d’une action par rapport au temps peut donner une indication de la vitesse à laquelle le prix change, ce qui est crucial pour prendre des décisions d’achat ou de vente.
Les mathématiques au quotidien
Ces anecdotes montrent que les dérivées et les intégrales ne sont pas seulement des concepts abstraits, mais des outils pratiques qui facilitent notre vie quotidienne. La prochaine fois que vous utiliserez un GPS ou que vous regarderez la météo, souvenez-vous que ces services sont rendus possibles grâce aux puissants concepts mathématiques que sont les dérivées et les intégrales.
Chapitre 11 : Conclusion : Les Mystères Infinis des Mathématiques
Au fil de cet article, nous avons exploré les dérivées et les intégrales sous différents angles. Nous avons découvert comment ces concepts, apparemment opposés, sont en réalité étroitement liés. Nous avons également vu comment ils influencent notre quotidien et leur importance dans des domaines aussi variés que la météo, la navigation GPS, et les finances.
Les dérivées et les intégrales sont bien plus que des outils mathématiques. Elles sont des clés pour comprendre le monde qui nous entoure. En continuant à explorer ces concepts et à les appliquer, nous pouvons découvrir de nouvelles perspectives et résoudre des problèmes complexes.
La beauté de la simplicité
Comme le disait Einstein, « Il faut toujours chercher à faire aussi simple que possible, mais pas plus. » Les dérivées et les intégrales incarnent cette quête de simplicité. Elles nous montrent que même les concepts les plus complexes peuvent être décomposés en idées plus simples, et que la mathématique est véritablement le langage de l’univers.
Merci d’avoir pris le temps de lire cet article. J’espère qu’il vous a inspiré et aidé à voir les mathématiques sous un nouvel angle. N’hésitez pas à partager vos questions, vos réflexions et vos découvertes. Ensemble, continuons à explorer les mystères infinis des mathématiques.
 Pourton.info
Pourton.info 



