Introduction
Pourquoi les Prévisions Météorologiques sont plus Complexes qu’une Épreuve de Mathématiques
Vous avez déjà maudit le météorologue parce que votre pique-nique a été gâché par la pluie alors que le soleil était prévu, ou que vous rêviez de voir la tempête du siècle qui n’est jamais arrivé ? Ne vous inquiétez pas, après avoir lu cet article, vous les remercierez pour chaque goutte épargnée ! Les prévisions météorologiques sont un défi quotidien qui requiert une ingéniosité mathématique et scientifique impressionnante. Ce n’est pas simplement une question de regarder le ciel et de faire une prédiction basée sur l’intuition. Non, c’est bien plus complexe.
Dans cet article, nous allons plonger dans les mathématiques sophistiquées qui sous-tendent les prévisions météorologiques. Nous verrons comment les météorologues utilisent des modèles numériques, l’assimilation de données, la paramétrisation, l’analyse spectrale, et même la théorie du chaos pour prévoir le temps. Vous découvrirez que les prévisions météo ne sont pas seulement une question de savoir s’il pleuvra demain, mais un véritable exploit scientifique qui mérite toute notre admiration.
Nous allons explorer comment les équations de Navier-Stokes décrivent le mouvement des fluides atmosphériques, comment les modèles numériques tentent de prédire l’avenir avec précision, et pourquoi même une petite erreur dans les conditions initiales peut conduire à des prévisions totalement différentes. Préparez-vous à voir la météo sous un nouveau jour, où chaque nuage, chaque goutte de pluie et chaque rayon de soleil sont le résultat de calculs complexes et d’une expertise mathématique avancée.
Prêts à embarquer dans ce voyage fascinant à travers les mathématiques des prévisions météorologiques ? Allons-y !
La Complexité de l’Atmosphère

L’Atmosphère : Une Soupe Géante en Perpétuel Mouvement
Imaginez l’atmosphère comme une soupe géante. Non seulement il y a tous les ingrédients classiques comme les nuages et le vent, mais c’est aussi une soupe qui a une fâcheuse tendance à se renverser et à se mélanger de manière chaotique. La raison pour laquelle prédire le temps est si complexe réside dans la nature même de l’atmosphère, un système dynamique où chaque petite perturbation peut avoir des effets considérables.
Les météorologues utilisent des équations mathématiques pour modéliser le comportement de l’atmosphère. Parmi les plus importantes, on trouve les équations de Navier-Stokes, qui décrivent le mouvement des fluides, comme l’air. Voici les équations complètes de Navier-Stokes pour un fluide incompressible :
![]()
![]()
Dans ces équations :
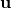 est le vecteur vitesse du fluide.
est le vecteur vitesse du fluide.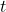 est le temps.
est le temps.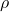 est la densité du fluide.
est la densité du fluide.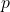 est la pression.
est la pression.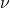 est la viscosité cinématique.
est la viscosité cinématique.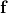 représente les forces extérieures (comme la gravité).
représente les forces extérieures (comme la gravité).
Ces équations sont fondamentales pour comprendre comment l’air se déplace dans l’atmosphère. Cependant, les résoudre directement est souvent impossible en raison de leur complexité. C’est pourquoi les météorologues utilisent des modèles numériques pour les approximations.
Un autre aspect crucial est l’effet de la chaleur et de la masse sur l’atmosphère. Les équations de conservation de l’énergie (ou première loi de la thermodynamique) et l’équation de continuité (conservation de la masse) sont également essentielles :
Équation de conservation de l’énergie :
![]()
Où :
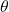 est la température potentielle.
est la température potentielle.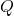 est la chaleur ajoutée par unité de masse.
est la chaleur ajoutée par unité de masse.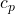 est la capacité calorifique à pression constante.
est la capacité calorifique à pression constante.
Équation de continuité (conservation de la masse) :
![]()
Ces équations montrent que l’atmosphère est un système où la dynamique des fluides, la thermodynamique et la conservation de la masse et de l’énergie interagissent de manière complexe. Cela explique pourquoi la prévision du temps est bien plus qu’une simple extrapolation des conditions actuelles.
Pour bien comprendre la difficulté des prévisions météorologiques, pensez à l’effet papillon. Un petit changement dans les conditions initiales peut entraîner des différences significatives dans les prévisions. C’est ce qui rend la prévision météorologique si fascinante et si complexe à la fois.
Les Modèles Numériques

Deviner la Fin d’une Série Netflix : Les Défis des Modèles Numériques Météorologiques
Les modèles numériques météorologiques sont un peu comme essayer de deviner la fin d’une série Netflix en regardant seulement les 5 premières minutes du premier épisode. Bonne chance avec ça ! En réalité, les modèles numériques sont des outils puissants qui utilisent des équations mathématiques pour prévoir l’état futur de l’atmosphère. Ils sont essentiels pour convertir des équations complexes en prévisions concrètes.
Les Modèles Globaux et Régionaux
Les modèles météorologiques se divisent en deux grandes catégories : les modèles globaux et les modèles régionaux. Les modèles globaux, comme le Global Forecast System (GFS) et le modèle de l’European Centre for Medium-Range Weather Forecasts (ECMWF), couvrent toute la planète. En revanche, les modèles régionaux, comme le Weather Research and Forecasting Model (WRF), se concentrent sur des zones plus petites et fournissent des prévisions plus détaillées pour ces régions spécifiques.
Les Équations de Base
Les modèles numériques résolvent les équations de Navier-Stokes, ainsi que d’autres équations de la dynamique des fluides et de la thermodynamique. Les équations principales incluent :
Équation du mouvement (Navier-Stokes) :
![]()
Équation de continuité (conservation de la masse) :
![]()
Équation de conservation de l’énergie :
![]()
Ces équations sont résolues sur une grille tridimensionnelle qui couvre la région d’intérêt. La résolution des modèles (la distance entre les points de la grille) influence directement la précision des prévisions. Plus la résolution est fine, plus les prévisions peuvent être détaillées, mais cela nécessite également plus de puissance de calcul.
Conditions Initiales et Effet Papillon
La précision des modèles numériques dépend fortement des conditions initiales, c’est-à-dire de la représentation de l’état actuel de l’atmosphère. Ces données initiales proviennent de diverses sources, telles que les stations météorologiques, les ballons-sondes, les satellites et les bouées océaniques. Un petit écart dans les conditions initiales peut entraîner des différences significatives dans les prévisions futures, illustrant l’effet papillon.
Effet papillon :
![]()
Où ![]() représente une petite perturbation à l’instant initial
représente une petite perturbation à l’instant initial ![]() et
et ![]() représente le changement à l’instant futur
représente le changement à l’instant futur ![]() .
.
Les modèles globaux utilisent des conditions initiales à grande échelle pour fournir des prévisions à long terme (jusqu’à 10-15 jours), tandis que les modèles régionaux se concentrent sur des prévisions à court terme et de haute précision pour des zones spécifiques.
En résumé
Les modèles numériques sont au cœur des prévisions météorologiques modernes. Ils transforment des équations mathématiques complexes en prévisions utiles, bien que la précision de ces prévisions dépende fortement des conditions initiales et de la résolution des modèles. C’est grâce à ces modèles que nous pouvons obtenir des prévisions météo qui, bien que parfois imparfaites, sont généralement fiables et nous aident à planifier nos activités quotidiennes.
L’Assimilation de Données

Réunir les Pièces du Puzzle : L’Art de l’Assimilation de Données
L’assimilation de données est une étape cruciale dans la prévision météorologique. Imaginez que vous essayez de reconstituer un puzzle avec des pièces venant de plusieurs boîtes différentes. Ah, et certains morceaux ont décidé de se cacher sous le canapé. L’assimilation de données, c’est un peu ça : prendre des informations fragmentées de différentes sources et les combiner pour obtenir une image cohérente de l’état actuel de l’atmosphère.
Sources de Données
Les météorologues collectent des données à partir de diverses sources :
- Stations météorologiques : Mesurent des variables comme la température, l’humidité, la pression atmosphérique et la vitesse du vent à des points spécifiques sur le globe.
- Ballons-sondes : Envoyés dans l’atmosphère pour collecter des données sur les profils de température, d’humidité et de vent à différentes altitudes.
- Satellites : Fournissent des données globales sur la couverture nuageuse, la température de surface de la mer, la concentration de vapeur d’eau et bien plus encore.
- Bouées océaniques : Mesurent la température de l’eau, la salinité et les courants océaniques.
Méthodes d’Assimilation de Données
Les données collectées doivent être intégrées dans les modèles numériques. Cela se fait par des méthodes mathématiques sophistiquées comme les filtres de Kalman et les méthodes variationnelles.
Filtre de Kalman :
![]()
Où :
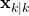 est l’estimation de l’état à l’instant
est l’estimation de l’état à l’instant 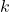 après l’assimilation des observations.
après l’assimilation des observations.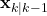 est l’estimation de l’état à l’instant
est l’estimation de l’état à l’instant 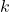 avant l’assimilation des observations.
avant l’assimilation des observations.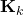 est le gain de Kalman, qui pondère l’importance relative des observations par rapport au modèle.
est le gain de Kalman, qui pondère l’importance relative des observations par rapport au modèle.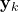 est le vecteur des observations à l’instant
est le vecteur des observations à l’instant 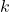 .
. est la matrice de transformation des états du modèle en observations.
est la matrice de transformation des états du modèle en observations.
Méthode variationnelle :
![]()
Où :
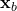 est l’état de fond (background state).
est l’état de fond (background state).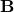 est la matrice de covariance des erreurs de l’état de fond.
est la matrice de covariance des erreurs de l’état de fond. est la matrice de covariance des erreurs d’observation.
est la matrice de covariance des erreurs d’observation.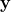 est le vecteur des observations.
est le vecteur des observations. est la matrice de transformation.
est la matrice de transformation.
Ces méthodes permettent de combiner les observations avec les prédictions du modèle pour obtenir une meilleure estimation de l’état actuel de l’atmosphère. C’est un processus essentiel car même les petites erreurs dans les conditions initiales peuvent se propager et amplifier dans les prévisions futures.
Harmoniser les Données pour des Prévisions Précises
L’assimilation de données est essentielle pour améliorer la précision des prévisions météorologiques. En combinant efficacement les données de différentes sources, les météorologues peuvent créer une image plus précise et cohérente de l’état actuel de l’atmosphère. Cela réduit les incertitudes et permet de mieux prévoir les évolutions futures.
Paramétrisation

Paramétrisation : Quand les Petits Bouts de Scotch Font Toute la Différence
Dans le monde des prévisions météorologiques, certains processus atmosphériques se produisent à des échelles trop petites pour être directement résolus par les modèles numériques. C’est là qu’intervient la paramétrisation. Imaginez que vous essayez de masquer un cadeau mal emballé avec de petits bouts de scotch : cela ne couvre pas tout, mais ça aide à rendre le tout présentable. De la même manière, les paramétrisations sont des approximations utilisées pour représenter ces processus sub-grid.
Pourquoi la Paramétrisation est-elle Nécessaire ?
Les modèles numériques ont une résolution limitée, ce qui signifie qu’ils ne peuvent pas capturer tous les détails des phénomènes météorologiques. Par exemple, les nuages, la turbulence et la convection se produisent souvent à des échelles plus petites que celles résolues par les modèles globaux. La paramétrisation permet de représenter ces processus de manière simplifiée.
Exemples de Paramétrisation
1. Paramétrisation des Nuages
Les nuages jouent un rôle crucial dans le climat et la météo, mais leur formation et leur dissipation sont des processus complexes. Les modèles utilisent des paramétrisations pour représenter la formation des nuages et les précipitations.
Equation simplifiée de la formation des nuages :
![]()
Où :
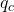 est la concentration de nuages.
est la concentration de nuages.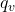 est la concentration de vapeur d’eau.
est la concentration de vapeur d’eau.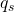 est la concentration de vapeur d’eau à saturation.
est la concentration de vapeur d’eau à saturation.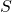 est une constante de formation des nuages.
est une constante de formation des nuages.
2. Paramétrisation de la Convection
La convection est un autre processus important qui se produit à une échelle trop petite pour être directement résolue. Elle est responsable de la formation des orages et des averses. La paramétrisation de la convection utilise des schémas qui représentent les effets collectifs de nombreuses cellules convectives.
Schéma simplifié de convection :
![]()
Où :
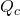 est le taux de chauffage convectif.
est le taux de chauffage convectif.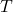 est la température.
est la température.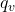 est la concentration de vapeur d’eau.
est la concentration de vapeur d’eau.
Limitations et Améliorations
Bien que les paramétrisations soient indispensables, elles introduisent des approximations qui peuvent entraîner des erreurs dans les prévisions. Les chercheurs travaillent constamment à améliorer ces schémas pour rendre les modèles plus précis. Cela inclut l’utilisation de nouvelles observations, de meilleures théories physiques et de techniques de modélisation avancées.
Pourquoi les Paramétrisations sont Cruciales pour les Modèles
Les paramétrisations permettent aux modèles numériques de représenter des processus essentiels de manière simplifiée, ce qui améliore la précision des prévisions sans nécessiter une résolution excessivement fine. Sans ces approximations, les modèles seraient incapables de fournir des prévisions utiles à une échelle pratique.
Analyse Spectrale

Analyse Spectrale : Trouver la Mélodie dans le Brouhaha Atmosphérique
L’analyse spectrale est un outil puissant utilisé par les météorologues pour décomposer les variables atmosphériques en fonctions d’ondes. Pensez à cela comme à écouter de la musique classique. Au début, tout semble être un fouillis de notes, mais avec un peu de pratique, on commence à reconnaître la mélodie et les motifs. L’analyse spectrale permet de trouver ces motifs cachés dans le brouhaha de l’atmosphère.
Qu’est-ce que l’Analyse Spectrale ?
L’analyse spectrale consiste à décomposer une série temporelle ou un champ spatial en une somme de sinusoïdes (ondes) de différentes fréquences et amplitudes. Cela permet de comprendre les différentes échelles de variabilité présentes dans les données météorologiques.
L’outil mathématique principal pour l’analyse spectrale est la transformation de Fourier :
![]()
Où :
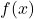 est la fonction d’origine (par exemple, la vitesse du vent en fonction du temps ou de la position).
est la fonction d’origine (par exemple, la vitesse du vent en fonction du temps ou de la position).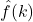 est la transformation de Fourier de
est la transformation de Fourier de 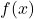 , représentant les amplitudes des différentes fréquences
, représentant les amplitudes des différentes fréquences 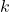 .
.
Application à la Météorologie
En météorologie, l’analyse spectrale est utilisée pour identifier et comprendre les ondes de grande échelle qui influencent le climat et les conditions météorologiques à long terme. Un exemple notable est l’onde de Rossby.
Ondes de Rossby
Les ondes de Rossby sont des oscillations à grande échelle dans l’atmosphère qui jouent un rôle crucial dans la circulation atmosphérique. Elles sont influencées par la rotation de la Terre et les variations de température.
L’équation des ondes de Rossby peut être écrite comme suit :
![]()
Où :
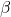 est le paramètre de Rossby, qui dépend de la variation de la force de Coriolis avec la latitude.
est le paramètre de Rossby, qui dépend de la variation de la force de Coriolis avec la latitude.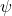 est la fonction de courant, représentant le flux d’air.
est la fonction de courant, représentant le flux d’air.
Décomposition en Modes Spectraux
La décomposition spectrale permet de séparer les différents modes de variabilité dans l’atmosphère. Par exemple, on peut identifier des modes de basse fréquence associés à des phénomènes climatiques à grande échelle, comme El Niño, et des modes de haute fréquence associés à des systèmes météorologiques plus locaux et transitoires.
Exemple de décomposition spectrale :
![]()
Où :
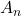 est l’amplitude du mode
est l’amplitude du mode 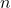 .
.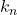 est le nombre d’onde.
est le nombre d’onde.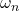 est la fréquence angulaire.
est la fréquence angulaire.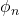 est la phase.
est la phase.
Utilité de l’Analyse Spectrale
L’analyse spectrale aide les météorologues à identifier les structures et les patterns dans les données météorologiques, ce qui permet de mieux comprendre les phénomènes à différentes échelles. Cela améliore la précision des prévisions à moyen et long terme et aide à identifier les anomalies climatiques.
Une Mélodie Mathématique dans le Chaos Atmosphérique
L’analyse spectrale permet de révéler les motifs cachés dans les données météorologiques, aidant les scientifiques à trouver une mélodie dans le chaos apparent de l’atmosphère. C’est un outil indispensable pour comprendre les processus à grande échelle qui influencent notre climat et notre météo.
Théorie du Chaos

La Théorie du Chaos : Prédire la Chute de la Tartine Beurrée
La théorie du chaos est un domaine fascinant des mathématiques qui traite de systèmes dynamiques extrêmement sensibles aux conditions initiales. C’est comme essayer de prédire où va tomber la tartine beurrée de votre enfant de deux ans. Vous savez qu’elle va tomber du côté du beurre, mais où exactement ? Mystère ! Dans le contexte de la météorologie, cela signifie que même de petites incertitudes dans les conditions initiales peuvent conduire à des prévisions très différentes à long terme.
Qu’est-ce que la Théorie du Chaos ?
La théorie du chaos se concentre sur les systèmes dynamiques non linéaires où des différences infinitésimales dans les conditions initiales peuvent entraîner des résultats largement divergents. Ce concept est souvent illustré par l’effet papillon, où le battement d’ailes d’un papillon au Brésil peut provoquer une tornade au Texas.
En météorologie, l’atmosphère est un système chaotique, ce qui rend les prévisions à long terme particulièrement difficiles. Une des manières de représenter cette sensibilité est à travers les attracteurs étranges, comme l’attracteur de Lorenz :
Système de Lorenz :
![]()
![]()
![]()
Où :
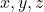 sont des variables d’état du système.
sont des variables d’état du système.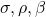 sont des paramètres du système.
sont des paramètres du système.
L’Effet Papillon en Météorologie
L’effet papillon, découvert par le météorologue Edward Lorenz, montre à quel point les prévisions météorologiques sont sensibles aux conditions initiales. Une infime variation dans les données initiales peut se traduire par une différence majeure dans les prévisions après quelques jours.
Représentation de l’effet papillon :
![]()
Où ![]() représente une petite perturbation à l’instant initial
représente une petite perturbation à l’instant initial ![]() et
et ![]() représente le changement à l’instant futur
représente le changement à l’instant futur ![]() .
.
Limites Pratiques des Prévisions
En raison de cette sensibilité, les prévisions météorologiques sont généralement fiables pour une période de 5 à 10 jours. Au-delà, l’incertitude augmente rapidement, rendant les prévisions de plus en plus imprécises. C’est pourquoi les météorologues fournissent souvent des prévisions probabilistes plutôt que déterministes, en indiquant la probabilité de différents scénarios météorologiques.
Prévisions probabilistes :
![]()
Où ![]() est la probabilité de l’événement
est la probabilité de l’événement ![]() .
.
Les Ensembles de Prévisions
Pour gérer l’incertitude et la sensibilité aux conditions initiales, les météorologues utilisent des ensembles de prévisions (ensemble forecasting). Cette méthode consiste à exécuter plusieurs simulations avec des conditions initiales légèrement différentes pour estimer la gamme possible des résultats futurs.
La Prédiction du Chaos
La théorie du chaos nous apprend que, malgré nos meilleurs efforts et nos modèles les plus sophistiqués, il y aura toujours une limite à la précision des prévisions météorologiques. Cela ne diminue en rien la valeur des prévisions à court terme et des tendances climatiques à long terme, mais cela nous rappelle l’importance de l’incertitude et de la probabilité dans la science du climat.
Prévoir l’Imprévisible
La théorie du chaos met en lumière les défis inhérents à la prévision météorologique. Elle nous montre que, même si nous ne pouvons pas éliminer complètement l’incertitude, nous pouvons utiliser des outils mathématiques sophistiqués pour mieux comprendre et prévoir les comportements complexes de l’atmosphère.
Applications Pratiques et Progrès

Des Prévisions pour Tous : De votre Chien à l’Aviation
Les prévisions météorologiques jouent un rôle essentiel dans de nombreux aspects de notre vie quotidienne, que ce soit pour décider de sortir avec un parapluie, planifier un barbecue ou gérer des opérations aériennes complexes. Les avancées technologiques et scientifiques continuent d’améliorer la précision et la fiabilité de ces prévisions, rendant notre vie plus sûre et plus confortable.
Utilisation Quotidienne des Prévisions Météorologiques
Agriculture Les agriculteurs dépendent des prévisions météorologiques pour décider quand planter, irriguer et récolter leurs cultures. Une bonne prévision peut optimiser la production et réduire les pertes.
Transport Aérien Les compagnies aériennes utilisent des prévisions météorologiques pour planifier les vols, éviter les turbulences et assurer la sécurité des passagers. Les pilotes sont informés des conditions météorologiques en temps réel, ce qui leur permet de prendre des décisions éclairées.
Gestion des Catastrophes Les prévisions météorologiques sont cruciales pour la gestion des catastrophes naturelles comme les ouragans, les inondations et les tempêtes. Les gouvernements et les organisations de secours utilisent ces informations pour évacuer les populations et coordonner les secours.
Loisirs Que ce soit pour planifier une randonnée, une sortie en bateau ou simplement décider quoi porter, les prévisions météorologiques influencent de nombreuses activités récréatives.
Avancées Technologiques
Superordinateurs Les superordinateurs jouent un rôle crucial dans les prévisions météorologiques. Ils permettent de traiter d’énormes quantités de données et de résoudre des équations complexes en un temps record. Par exemple, le Centre Européen pour les Prévisions Météorologiques à Moyen Terme (ECMWF) utilise des superordinateurs parmi les plus puissants du monde pour ses prévisions.
Satellites Les satellites météorologiques fournissent des données globales en temps réel sur la couverture nuageuse, les températures de surface, les niveaux de vapeur d’eau et bien plus encore. Ces informations sont essentielles pour améliorer la précision des modèles météorologiques.
Réseaux de Capteurs Les réseaux de capteurs, comprenant des stations météorologiques, des ballons-sondes et des bouées océaniques, collectent des données à haute résolution sur les conditions atmosphériques et océaniques. Ces données alimentent les modèles et permettent d’affiner les prévisions.
Progrès dans la Modélisation
Modèles à Haute Résolution Les progrès en matière de puissance de calcul ont permis le développement de modèles météorologiques à haute résolution, capables de capturer des détails fins et des phénomènes locaux. Cela améliore la précision des prévisions pour des régions spécifiques.
Ensembles de Prévisions Les ensembles de prévisions (ensemble forecasting) permettent de gérer l’incertitude en exécutant plusieurs simulations avec des conditions initiales légèrement différentes. Cela fournit une gamme de résultats possibles et permet d’estimer la probabilité des différents scénarios météorologiques.
Intelligence Artificielle L’intelligence artificielle (IA) et l’apprentissage automatique sont de plus en plus utilisés pour améliorer les prévisions météorologiques. Ces technologies peuvent analyser de vastes ensembles de données et détecter des patterns complexes, contribuant ainsi à affiner les prévisions.
Prévisions Météorologiques : Un Outil Indispensable
Les prévisions météorologiques sont devenues un outil indispensable dans de nombreux domaines, grâce aux progrès technologiques et scientifiques. Elles nous aident à planifier notre quotidien, à assurer la sécurité des transports, à gérer les ressources agricoles et à faire face aux catastrophes naturelles. Les avancées continues dans ce domaine promettent de rendre les prévisions encore plus précises et fiables.
Vers des Prévisions de Plus en Plus Précises
Grâce à l’intégration de technologies avancées et à l’amélioration continue des modèles, les prévisions météorologiques ne cessent de s’améliorer. Cela permet non seulement de mieux comprendre et anticiper les phénomènes météorologiques, mais aussi de prendre des décisions plus éclairées dans divers aspects de notre vie quotidienne.
Conclusion

Devenez un Ami des Météorologues : La Science derrière les Prévisions
Alors, la prochaine fois que vous vérifiez la météo et que vous voyez de la pluie alors que vous aviez prévu un barbecue, souvenez-vous de toute la science et des mathématiques qui se cachent derrière ces prévisions. Et peut-être gardez un parapluie à portée de main, juste au cas où.
Récapitulatif
Tout au long de cet article, nous avons exploré les différentes facettes des prévisions météorologiques, en mettant en lumière la complexité et la sophistication des mathématiques et des sciences qui sous-tendent ce domaine fascinant. De l’utilisation des équations de Navier-Stokes pour modéliser les mouvements atmosphériques, à l’assimilation de données, en passant par la paramétrisation des processus sub-grid et l’analyse spectrale, chaque étape joue un rôle crucial pour transformer des observations brutes en prévisions utiles.
Nous avons également discuté de la théorie du chaos et de son impact sur la précision des prévisions à long terme, ainsi que des nombreuses applications pratiques des prévisions météorologiques, rendues possibles par les avancées technologiques et les superordinateurs.
Réflexion
La science des prévisions météorologiques est un domaine en constante évolution, où chaque nouvelle découverte et chaque avancée technologique contribuent à améliorer notre compréhension de l’atmosphère. C’est un rappel constant de l’importance des mathématiques et des sciences dans notre vie quotidienne, et de l’ingéniosité humaine nécessaire pour transformer des phénomènes naturels complexes en informations pratiques.
À la Croisée des Mathématiques et de la Météorologie
Les prévisions météorologiques sont un parfait exemple de la manière dont les mathématiques, la physique et la technologie peuvent converger pour résoudre des problèmes complexes et améliorer notre quotidien. Les météorologues, avec leur expertise et leur dévouement, travaillent sans relâche pour affiner leurs modèles et fournir des prévisions de plus en plus précises. La prochaine fois que vous vérifierez la météo, prenez un moment pour apprécier le travail colossal qui se cache derrière ces simples chiffres et pictogrammes.
Appel à l’Action
Pour ceux qui sont passionnés par les mathématiques et les sciences, la météorologie offre un champ d’application riche et varié où vous pouvez mettre à profit vos compétences et contribuer à des avancées significatives. Que vous soyez étudiant, chercheur ou simplement curieux, n’hésitez pas à explorer davantage ce domaine captivant. Peut-être deviendrez-vous, vous aussi, un ami des météorologues.
Remerciements et Bibliographie
Merci d’avoir pris le temps de lire cet article. J’espère qu’il vous a permis de mieux comprendre les défis et les merveilles des prévisions météorologiques. Pour ceux qui souhaitent approfondir leurs connaissances, voici quelques ressources et références pour aller plus loin.
- Livres et Articles
- « Théorème vivant » de Cédric Villani : Une plongée dans le monde des mathématiques, accessible et fascinante.
- « Atmospheric Modeling, Data Assimilation and Predictability » par Eugenia Kalnay : Un ouvrage complet sur les modèles et les méthodes d’assimilation de données.
- Sites Web et Cours en Ligne
 Pourton.info
Pourton.info 



