Introduction : Pourquoi les Fonctions de Bessel ?
Ah, les fonctions de Bessel ! Elles sont aux mathématiques ce que la symphonie est à la musique : complexes, élégantes, et omniprésentes dans les phénomènes naturels. Imaginez-vous être un ingénieur ou un physicien du 19ème siècle, découvrant les mystères de l’univers, et tombant soudain sur cette équation mystérieuse. Pas de panique, car Friedrich Bessel est là pour vous guider, tel un maître Jedi des nombres.
Les fonctions de Bessel apparaissent dans des problèmes qui présentent des symétries cylindriques ou sphériques. Leur importance réside dans leur capacité à simplifier des équations compliquées, transformant des monstres mathématiques en créatures dociles.
Prenons par exemple un cas où vous étudiez la propagation des ondes électromagnétiques dans un guide d’ondes cylindrique. Au lieu de vous battre avec une équation différentielle inextricable, les fonctions de Bessel viennent à votre secours pour rendre le problème plus tractable.
Mais avant de plonger plus profondément, un peu d’histoire ! Friedrich Wilhelm Bessel, l’astronome et mathématicien allemand, a introduit ces fonctions dans le cadre de ses travaux sur les mouvements planétaires. Bien qu’il ait été principalement un astronome, ses contributions mathématiques ont laissé un impact durable.
L’Équation Différentielle de Bessel : La Formule Magique
Plongeons maintenant dans le vif du sujet avec l’équation différentielle de Bessel, un véritable bijou des mathématiques. Cette équation peut sembler intimidante à première vue, mais ne vous inquiétez pas, nous allons la décortiquer ensemble.
L’équation différentielle de Bessel s’écrit comme suit :
![]()
où ![]() est un nombre complexe arbitraire appelé l’ordre de la fonction de Bessel.
est un nombre complexe arbitraire appelé l’ordre de la fonction de Bessel.
Voyons ce que chaque terme signifie :
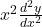 : Ce terme représente la contribution de la deuxième dérivée de
: Ce terme représente la contribution de la deuxième dérivée de 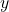 par rapport à
par rapport à 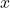 , pondérée par
, pondérée par 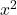 . En d’autres termes, il tient compte de la courbure de la fonction.
. En d’autres termes, il tient compte de la courbure de la fonction.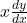 : Ici, nous avons la première dérivée de
: Ici, nous avons la première dérivée de 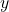 , pondérée par
, pondérée par 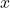 . Ce terme reflète la pente de la fonction.
. Ce terme reflète la pente de la fonction.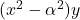 : Ce dernier terme combine
: Ce dernier terme combine 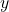 avec une pondération dépendant de
avec une pondération dépendant de 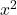 et de l’ordre
et de l’ordre 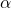 .
.
L’équation de Bessel est une équation différentielle ordinaire linéaire du second ordre. Elle est homogène, ce qui signifie qu’elle ne contient pas de terme indépendant de ![]() . Les solutions de cette équation, les fameuses fonctions de Bessel, sont cruciales pour de nombreux problèmes pratiques.
. Les solutions de cette équation, les fameuses fonctions de Bessel, sont cruciales pour de nombreux problèmes pratiques.
L’Importance de l’Ordre 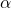
L’ordre ![]() joue un rôle clé dans l’équation de Bessel. Il détermine la forme des solutions et leur comportement. Par exemple, pour des valeurs entières de
joue un rôle clé dans l’équation de Bessel. Il détermine la forme des solutions et leur comportement. Par exemple, pour des valeurs entières de ![]() , les solutions ont des propriétés particulières et sont souvent utilisées dans des applications physiques spécifiques.
, les solutions ont des propriétés particulières et sont souvent utilisées dans des applications physiques spécifiques.
Laissez-moi vous raconter une petite anecdote. Friedrich Bessel, dans ses travaux sur les mouvements planétaires, a découvert que pour résoudre les équations décrivant les trajectoires des planètes, il devait utiliser des fonctions spéciales qui n’étaient pas encore bien comprises. En explorant ces fonctions, il a ouvert la porte à une nouvelle branche des mathématiques, désormais essentielle dans de nombreux domaines.
Voyage au Cœur des Solutions : 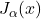 et
et 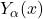

Les solutions de l’équation de Bessel sont fascinantes et elles se déclinent principalement en deux types : les fonctions de Bessel de première espèce ![]() et les fonctions de Bessel de seconde espèce
et les fonctions de Bessel de seconde espèce ![]() . Chacune de ces fonctions a ses propres caractéristiques et applications.
. Chacune de ces fonctions a ses propres caractéristiques et applications.
Fonctions de Bessel de Première Espèce 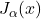
Les fonctions de Bessel de première espèce, notées ![]() , sont les solutions régulières à l’origine (c’est-à-dire lorsque
, sont les solutions régulières à l’origine (c’est-à-dire lorsque ![]() ). Elles sont particulièrement utiles dans les problèmes de conditions aux limites où la régularité à l’origine est requise.
). Elles sont particulièrement utiles dans les problèmes de conditions aux limites où la régularité à l’origine est requise.
L’expression générale pour ![]() peut être donnée par la série de Frobenius :
peut être donnée par la série de Frobenius :
![]()
où ![]() est la fonction Gamma, une généralisation de la factorielle.
est la fonction Gamma, une généralisation de la factorielle.
Pour les valeurs entières de ![]() , la fonction
, la fonction ![]() peut être simplifiée et est souvent utilisée pour décrire des phénomènes physiques tels que les ondes dans un cylindre.
peut être simplifiée et est souvent utilisée pour décrire des phénomènes physiques tels que les ondes dans un cylindre.
Fonctions de Bessel de Seconde Espèce 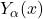
Les fonctions de Bessel de seconde espèce, notées ![]() , aussi appelées fonctions de Neumann ou de Weber, sont singulières à l’origine. Elles complètent les solutions de première espèce pour former une base complète des solutions de l’équation de Bessel.
, aussi appelées fonctions de Neumann ou de Weber, sont singulières à l’origine. Elles complètent les solutions de première espèce pour former une base complète des solutions de l’équation de Bessel.
Une représentation intégrale pour ![]() est donnée par :
est donnée par :
![]()
Pour les valeurs entières de ![]() , cette expression nécessite une prise en compte spéciale des limites, mais le concept général reste le même.
, cette expression nécessite une prise en compte spéciale des limites, mais le concept général reste le même.
Les Propriétés des Fonctions de Bessel
Voici quelques propriétés intéressantes des fonctions de Bessel :
- Orthogonalité : Les fonctions de Bessel de différents ordres
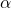 sont orthogonales sur des intervalles spécifiques, ce qui est très utile dans les développements en série de fonctions.
sont orthogonales sur des intervalles spécifiques, ce qui est très utile dans les développements en série de fonctions. - Zéros : Les fonctions de Bessel
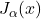 et
et 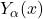 ont des zéros à des positions spécifiques. Ces zéros sont importants dans la résolution de problèmes physiques où les conditions aux limites imposent des solutions nulles à certains points.
ont des zéros à des positions spécifiques. Ces zéros sont importants dans la résolution de problèmes physiques où les conditions aux limites imposent des solutions nulles à certains points.
Utilisation Pratique
Imaginons un problème pratique. Vous êtes un ingénieur acousticien et vous devez modéliser la vibration d’une membrane circulaire, comme celle d’un tambour. En utilisant les fonctions de Bessel, vous pouvez trouver les modes de vibration de la membrane, c’est-à-dire les fréquences auxquelles la membrane résonne. Cela vous permet de concevoir des instruments de musique ou d’analyser les propriétés acoustiques de matériaux.
Applications Pratiques : Quand la Théorie Rencontre le Réel

Les fonctions de Bessel ne sont pas seulement des curiosités mathématiques ; elles jouent un rôle crucial dans de nombreux domaines scientifiques et techniques. Explorons quelques-unes de leurs applications les plus fascinantes.
Électromagnétisme : Les Ondes et les Cylindres, une Histoire d’Amour
Dans le domaine de l’électromagnétisme, les fonctions de Bessel sont essentielles pour résoudre les équations de Maxwell dans des géométries cylindriques. Prenons l’exemple des guides d’ondes cylindriques, utilisés dans les télécommunications pour diriger les ondes électromagnétiques.
Lorsqu’une onde électromagnétique se propage dans un guide d’ondes cylindrique, les composantes du champ électrique et du champ magnétique doivent satisfaire l’équation de Bessel. Les solutions aux modes de propagation dans ces guides sont souvent exprimées en termes de fonctions de Bessel de première et de seconde espèce.
Pour illustrer, considérons un guide d’ondes circulaire avec un rayon ![]() . Les modes TE (Transverse Electric) et TM (Transverse Magnetic) peuvent être décrits par :
. Les modes TE (Transverse Electric) et TM (Transverse Magnetic) peuvent être décrits par :
![]()
où ![]() est la fonction de Bessel de première espèce,
est la fonction de Bessel de première espèce, ![]() est le paramètre de propagation radial, et
est le paramètre de propagation radial, et ![]() est la constante de propagation le long de l’axe du guide.
est la constante de propagation le long de l’axe du guide.
Mécanique Quantique : La Danse des Particules en Géométrie Cylindrique
En mécanique quantique, les fonctions de Bessel apparaissent fréquemment dans la résolution de l’équation de Schrödinger pour des potentiels ayant une symétrie cylindrique ou sphérique. Par exemple, dans le cas d’un puits de potentiel cylindrique, les solutions radiales de l’équation de Schrödinger peuvent être exprimées en termes de fonctions de Bessel.
Supposons que nous ayons une particule confinée dans un puits cylindrique de rayon ![]() . L’équation radiale de Schrödinger pour une particule libre dans ce puits est :
. L’équation radiale de Schrödinger pour une particule libre dans ce puits est :
![]()
où ![]() est la fonction radiale, et
est la fonction radiale, et ![]() est le nombre d’onde. Les solutions de cette équation sont les fonctions de Bessel
est le nombre d’onde. Les solutions de cette équation sont les fonctions de Bessel ![]() et
et ![]() .
.
Vibrations et Acoustique : Du Tambour à la Salle de Concert
Les fonctions de Bessel sont également cruciales pour l’analyse des vibrations et des ondes acoustiques dans des structures cylindriques. Prenons par exemple une membrane circulaire, comme celle d’un tambour. Les modes de vibration de cette membrane sont décrits par les fonctions de Bessel.
Lorsque la membrane vibre, ses déplacements peuvent être modélisés par une équation différentielle partielle dont les solutions sont des fonctions de Bessel de première espèce ![]() . Les fréquences naturelles de vibration, ou modes propres, sont déterminées par les zéros de ces fonctions.
. Les fréquences naturelles de vibration, ou modes propres, sont déterminées par les zéros de ces fonctions.
Pour une membrane de rayon ![]() , les modes de vibration sont donnés par :
, les modes de vibration sont donnés par :
![]()
où ![]() est le
est le ![]() -ième zéro de la fonction de Bessel
-ième zéro de la fonction de Bessel ![]() , et
, et ![]() est la fréquence angulaire du mode.
est la fréquence angulaire du mode.
Ces concepts ne sont pas seulement théoriques. Ils sont appliqués dans la conception des instruments de musique, l’acoustique des salles de concert, et même dans l’analyse des vibrations des structures architecturales.
Anecdotes Mathématiques : Bessel à Travers le Temps

Les fonctions de Bessel ont une histoire riche et des applications surprenantes. Voici quelques anecdotes et curiosités qui montrent à quel point ces fonctions sont fascinantes.
Bessel et les Étoiles
Friedrich Wilhelm Bessel n’a pas découvert ses fameuses fonctions par hasard. Il était avant tout un astronome passionné. En 1838, il a été le premier à mesurer la distance d’une étoile en dehors de notre système solaire en utilisant la parallaxe stellaire. Cette étoile, 61 Cygni, est désormais connue sous le nom de « l’étoile de Bessel ».
Mais quel est le lien avec les fonctions de Bessel ? En travaillant sur les mouvements des planètes et des étoiles, Bessel a rencontré des équations différentielles complexes qui nécessitaient des solutions particulières. C’est ainsi qu’il a introduit ces fonctions qui portent désormais son nom.
Diffusion de la Chaleur : Une Problème de Tambour
Imaginez que vous êtes en train de cuire une pizza et que vous voulez comprendre comment la chaleur se diffuse à travers la pâte circulaire. La diffusion de la chaleur dans une plaque circulaire est un problème classique qui peut être résolu à l’aide des fonctions de Bessel.
La température ![]() dans une plaque circulaire uniforme peut être modélisée par l’équation de la chaleur en coordonnées cylindriques :
dans une plaque circulaire uniforme peut être modélisée par l’équation de la chaleur en coordonnées cylindriques :
![]()
Pour une plaque circulaire homogène et isotrope (où ![]() ne dépend pas de
ne dépend pas de ![]() ), la solution peut être exprimée en termes de fonctions de Bessel :
), la solution peut être exprimée en termes de fonctions de Bessel :
![]()
où ![]() sont les zéros de la fonction de Bessel
sont les zéros de la fonction de Bessel ![]() et
et ![]() est le rayon de la plaque.
est le rayon de la plaque.
Pression et Fluides : Les Tuyaux ne sont Pas si Simples
Dans l’étude des fluides incompressibles, les fonctions de Bessel jouent également un rôle crucial. Supposons que vous ayez un fluide se déplaçant dans un tuyau cylindrique. Pour analyser la distribution de la pression et la vitesse du fluide, vous devez résoudre l’équation de Navier-Stokes en coordonnées cylindriques.
La composante radiale de la vitesse ![]() dans un tuyau cylindrique peut être exprimée en termes de fonctions de Bessel. Par exemple, pour un écoulement oscillant, la solution peut ressembler à ceci :
dans un tuyau cylindrique peut être exprimée en termes de fonctions de Bessel. Par exemple, pour un écoulement oscillant, la solution peut ressembler à ceci :
![]()
où ![]() est un paramètre lié à la fréquence de l’oscillation
est un paramètre lié à la fréquence de l’oscillation ![]() et au rayon du tuyau
et au rayon du tuyau ![]() .
.
Ces exemples montrent que les fonctions de Bessel sont omniprésentes dans les sciences appliquées. Elles apparaissent dans des situations allant de la cuisson de votre pizza à l’analyse des écoulements de fluides dans les tuyaux industriels.
Visualisation : Une Galerie de Fonctions de Bessel

La visualisation est un outil puissant pour comprendre et apprécier les mathématiques. Les fonctions de Bessel ne font pas exception. Voyons comment elles se comportent et pourquoi la visualisation est si utile.
Graphiques des Fonctions 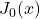 ,
, 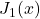 ,
, 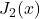
Pour commencer, jetons un œil aux premières fonctions de Bessel de première espèce ![]() pour
pour ![]() .
.
- Fonction de Bessel de Première Espèce
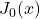
La fonction ![]() est souvent utilisée pour décrire les phénomènes ondulatoires en symétrie cylindrique. Voici son expression sous forme de série :
est souvent utilisée pour décrire les phénomènes ondulatoires en symétrie cylindrique. Voici son expression sous forme de série :
![]()
Visualisons-la :
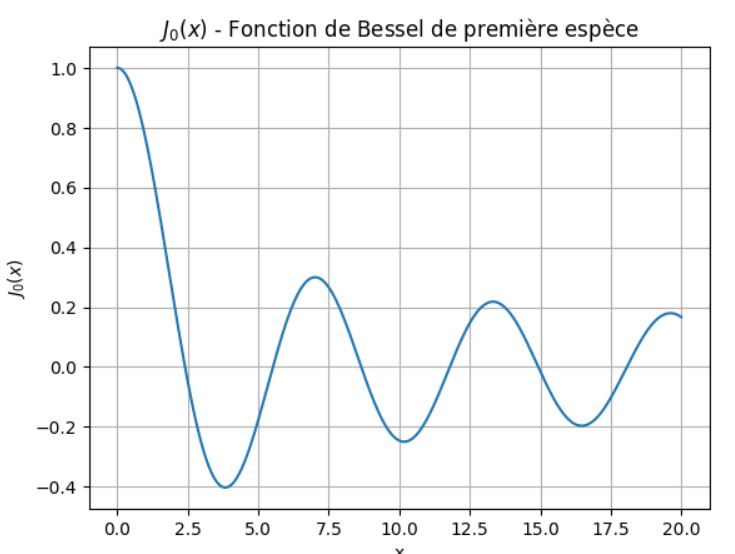
- Fonction de Bessel de Première Espèce
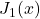
La fonction ![]() est la suivante dans la série. Elle est utile pour modéliser les phénomènes vibratoires et acoustiques.
est la suivante dans la série. Elle est utile pour modéliser les phénomènes vibratoires et acoustiques.
![]()
Visualisons-la :

- Fonction de Bessel de Première Espèce
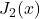
La fonction ![]() continue la série. Elle apparaît dans divers contextes scientifiques, notamment en mécanique des fluides.
continue la série. Elle apparaît dans divers contextes scientifiques, notamment en mécanique des fluides.
![]()
Visualisons-la :
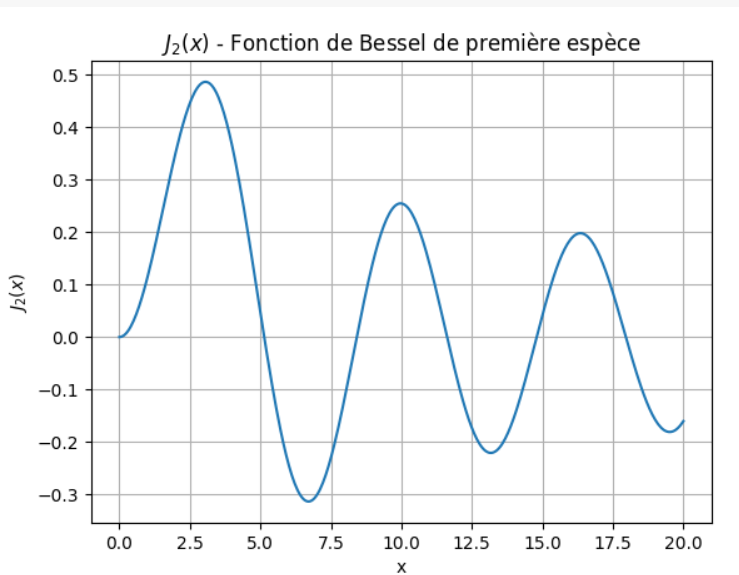
Pourquoi la Visualisation Aide à Comprendre les Mathématiques
- Intuition Visuelle : Voir la forme d’une fonction aide à comprendre son comportement. Par exemple, les oscillations et les zéros des fonctions de Bessel sont beaucoup plus faciles à saisir visuellement qu’à travers des séries infinies ou des représentations intégrales.
- Identification des Propriétés : La visualisation permet d’identifier des propriétés importantes, comme l’orthogonalité, les zéros et la symétrie. Par exemple, on peut voir que les fonctions de Bessel
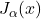 oscillent et décroissent avec l’augmentation de
oscillent et décroissent avec l’augmentation de 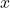 .
. - Applications Pratiques : Dans des applications pratiques, comme l’ingénierie ou la physique, les graphiques des fonctions de Bessel peuvent être utilisés pour comparer des modèles théoriques avec des données expérimentales. Cela permet de vérifier si les solutions théoriques correspondent bien aux observations.
- Engagement des Étudiants : Pour les étudiants, la visualisation rend les mathématiques plus engageantes et moins abstraites. Voir les graphiques de fonctions complexes peut susciter l’intérêt et faciliter l’apprentissage.
Conclusion : La Beauté Cachée des Fonctions de Bessel

Les fonctions de Bessel sont des outils mathématiques puissants et élégants qui se retrouvent dans une multitude de domaines scientifiques et techniques. Leur découverte et leur étude ont non seulement enrichi notre compréhension des équations différentielles mais ont aussi fourni des solutions pratiques à des problèmes complexes dans des contextes variés allant de l’électromagnétisme à la mécanique quantique.
Invitation à Poursuivre l’Exploration
Les fonctions de Bessel, comme vous pouvez le voir, sont bien plus que de simples solutions d’équations différentielles. Elles sont des outils mathématiques essentiels qui nous aident à comprendre et à modéliser le monde autour de nous. Que vous soyez étudiant, ingénieur ou simplement un amateur de mathématiques, je vous encourage à plonger plus profondément dans l’étude de ces fonctions fascinantes.
Continuez à explorer, à poser des questions, et à découvrir comment les mathématiques peuvent transformer votre vision du monde. Les fonctions de Bessel ne sont qu’un exemple parmi tant d’autres de la beauté et de l’utilité des mathématiques.
 Pourton.info
Pourton.info 



