Pourton.info 
Introduction à la Probabilité Bayésienne
Bienvenue dans le monde fascinant des probabilités, où chaque événement a sa propre histoire à raconter. Les probabilités nous permettent de mesurer l’incertitude et de prendre des décisions éclairées dans des situations d’incertitude. Avant de plonger dans les subtilités de la formule de Bayes, comprenons d’abord ce qu’est la probabilité.
Qu’est-ce que la Probabilité?
La probabilité mesure la fréquence à laquelle un événement est susceptible de se produire par rapport à toutes les issues possibles. Cela nous donne une base pour calculer des événements dans des conditions incertaines. Par exemple, la probabilité de tirer une carte as d’un jeu de 52 cartes est de 
, puisqu’il y a quatre as dans le jeu.
La Formule de Bayes : Un Premier Aperçu
Au cœur de notre sujet se trouve la formule de Bayes, un principe fondamental en théorie des probabilités qui permet de réviser les probabilités à la lumière de nouvelles preuves. Voici la formule en toute sa splendeur :
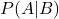est la probabilité de l’événement 
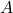sachant que 
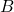s’est produit.
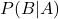est la probabilité de l’événement 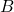sachant que 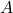s’est produit.
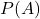est la probabilité initiale de l’événement 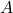avant de connaître l’issue de .
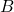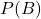est la probabilité totale de l’événement .
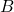Cette formule est plus qu’une simple équation ; c’est un outil puissant pour mettre à jour nos croyances en fonction de nouvelles informations. Que ce soit en sciences, en ingénierie, en économie ou même dans notre vie quotidienne, la capacité de réajuster nos attentes face à de nouvelles données est essentielle.
Dans les chapitres suivants, nous explorerons plus en détail le développement historique de cette formule, ses applications pratiques, et comment elle continue d’influencer divers domaines de recherche aujourd’hui.
Thomas Bayes : L’Homme Derrière la Formule
Thomas Bayes était un statisticien et un pasteur presbytérien anglais du XVIIIe siècle, dont le travail posthume a posé les fondations de ce que nous connaissons aujourd’hui sous le nom de théorème de Bayes. Peu de détails de sa vie personnelle sont connus, mais son impact sur les statistiques est indéniable.
Qui était Thomas Bayes?
Né en 1701 à Londres, Bayes a développé un intérêt précoce pour les mathématiques et la logique, qui s’est manifesté tout au long de sa vie. En plus de ses devoirs ecclésiastiques, il s’est consacré à des études mathématiques, notamment en probabilité. Bayes était un membre respecté de la Royal Society, témoignant de son influence et de son respect dans le milieu scientifique de l’époque.
La Génèse de sa Célèbre Formule
Le théorème de Bayes n’a été publié qu’après sa mort, en 1763, grâce aux efforts de son ami Richard Price. Ce dernier a découvert le manuscrit de Bayes et a décidé qu’il était trop important pour rester inconnu. Le travail de Bayes concernait principalement la manière de déduire la probabilité d’un événement futur, basée sur son occurrence passée et d’autres connaissances préalables.
La formulation originale par Bayes cherchait à résoudre un problème d’inversion de probabilité : comment déduire les causes à partir des effets observés. Le résultat fut une méthode révolutionnaire pour réévaluer les probabilités à la lumière de nouvelles preuves, illustrée par sa formule :
L’Héritage de Bayes
Bien que le théorème de Bayes soit resté relativement obscur pendant plusieurs décennies après sa publication, il a finalement été reconnu comme une pierre angulaire de la théorie statistique moderne. Aujourd’hui, cette formule est fondamentale dans de nombreux domaines scientifiques et pratiques, facilitant des décisions basées sur l’accumulation et l’analyse de preuves probantes.
Le Principe de la Formule de Bayes
Maintenant que nous avons une idée de l’homme derrière le théorème, penchons-nous sur la mécanique de la formule de Bayes et son application pratique. Ce chapitre expliquera la formule en termes simples et illustrera son usage à travers des exemples typiques.
Décryptage de la Formule
La formule de Bayes est essentielle pour comprendre comment les probabilités conditionnelles fonctionnent et comment elles peuvent être utilisées pour mettre à jour nos croyances en fonction de nouvelles informations. Réexaminons la formule :
Chaque terme a un rôle spécifique :
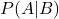- est la probabilité postérieure, ou la probabilité de 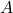après avoir pris en compte .
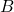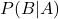- est la probabilité de voir 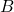si 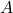est vrai.
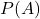- est la probabilité a priori de 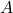, basée sur des connaissances antérieures.
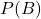- est la probabilité totale de 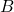, qui agit comme un facteur de normalisation pour assurer que les probabilités somment correctement à un.
Exemple Illustratif : Test Médical
Imaginons que nous voulons évaluer la probabilité qu’une personne ait une maladie basée sur le résultat d’un test médical. Supposons que :
- La probabilité qu’une personne choisie au hasard ait la maladie est de 1%, soit
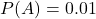. - La probabilité d’un résultat positif au test si la personne a la maladie est de 99%, soit
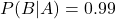. - La probabilité d’un résultat positif au test si la personne n’a pas la maladie (faux positif) est de 5%, donc
.
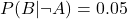Pour trouver , la probabilité totale de tester positif, nous utilisons :
Enfin, appliquons la formule de Bayes pour trouver la probabilité que la personne soit malade sachant qu’elle a testé positif :
Cet exemple montre que même avec un test très précis, la probabilité qu’une personne soit réellement malade après un test positif n’est que de 16.67%, soulignant l’importance de la probabilité pré-test (a priori).
Importance de la Mise à Jour des Probabilités
Cet exemple illustre bien comment la formule de Bayes nous permet de mettre à jour nos estimations probabilistiques à la lumière de nouvelles informations. Elle montre également l’importance des probabilités a priori dans l’évaluation des résultats.
Applications Modernes de la Formule de Bayes
La formule de Bayes n’est pas seulement un concept théorique fascinant; elle s’applique aussi à une variété incroyable de situations pratiques. De la science des données à la médecine, en passant par la prise de décision en affaires, le théorème de Bayes joue un rôle crucial dans la compréhension et la gestion de l’incertitude.
Statistique et Science des Données
En statistique, la formule de Bayes est la pierre angulaire de l’inférence bayésienne, qui utilise les probabilités pour estimer les paramètres et faire des prédictions. Par exemple, en modélisation prédictive, elle permet de mettre à jour continuellement les prédictions à mesure que de nouvelles données sont disponibles. Cela rend les modèles plus flexibles et réactifs aux changements.
Diagnostic Médical
En médecine, comme vu précédemment, la formule de Bayes aide les médecins à interpréter les résultats des tests diagnostiques. En combinant la connaissance des taux de prévalence d’une maladie et la sensibilité ainsi que la spécificité des tests, les professionnels de santé peuvent mieux évaluer les risques et prendre des décisions éclairées sur le traitement à suivre.
Systèmes de Recommandation
Les systèmes de recommandation, comme ceux utilisés par Netflix ou Amazon, utilisent aussi des techniques bayésiennes pour prédire ce qu’un utilisateur pourrait aimer regarder ou acheter ensuite. En analysant les interactions passées et les préférences de l’utilisateur, ces systèmes ajustent continuellement leurs recommandations pour mieux correspondre aux goûts de l’utilisateur.
Filtre Anti-Spam
Le filtrage de spam dans les e-mails utilise également la formule de Bayes pour identifier les messages indésirables. En calculant la probabilité qu’un message soit un spam basé sur la fréquence de certains mots, les filtres peuvent efficacement trier les e-mails et réduire le nombre de spams qui atteignent la boîte de réception des utilisateurs.
Exploration et Recherche
Que ce soit en finance, en écologie, ou même en astrophysique, la formule de Bayes aide à modeler l’incertitude et à prendre des décisions basées sur des données incomplètes ou incertaines. Elle permet aux chercheurs de tester des hypothèses et de réviser leurs théories en réponse à de nouvelles preuves ou données.
Conclusion : La Portée et l’Impact de Bayes
Le théorème de Bayes, au-delà d’une simple équation mathématique, est une manière de penser qui transcende les disciplines et les siècles. Il permet une compréhension dynamique et adaptable du monde, essentielle dans une société où l’information est abondante et souvent fragmentaire.
Réévaluation de la Connaissance
Le principal enseignement du théorème de Bayes est sa capacité à intégrer de nouvelles informations pour réviser nos croyances ou connaissances antérieures. Cette approche est fondamentale non seulement en science, où les théories sont constamment mises à l’épreuve et actualisées, mais aussi dans notre vie quotidienne, où nous faisons constamment face à des décisions sous incertitude.
Influence Prolongée dans le Temps
Bien que Thomas Bayes ait vécu au XVIIIe siècle, l’élégance et la pertinence de sa formule perdurent. L’inférence bayésienne est devenue un outil indispensable dans le kit méthodologique des scientifiques, des analystes et des décideurs. Elle incarne la convergence de l’histoire et de l’innovation, prouvant que les idées puissantes peuvent traverser le temps et continuer à influencer de manière significative.
Un Avenir Bayésien
À l’avenir, avec l’augmentation des données disponibles et la complexité des problèmes mondiaux, les méthodes bayésiennes joueront un rôle encore plus crucial. Elles permettront de naviguer dans des mers d’incertitude avec une boussole fiable, en adaptant nos modèles et prédictions à mesure que de nouvelles données émergent.
En résumé, la formule de Bayes n’est pas seulement un outil mathématique; c’est une philosophie de l’interrogation continue et de l’adaptation, une méthode pour affiner notre compréhension du monde d’une manière quantifiée et mesurée. Elle nous enseigne que le savoir n’est pas statique, mais un voyage de découverte continuel.
