Référence à son papier « Hydra Game », c’est méta, c’est beau.
C’est l’histoire d’un Everest mathématique que certains tentent de gravir en tongs.
La conjecture de Syracuse (aussi appelée problème de Collatz, ou problème ![]() ) est d’une simplicité désarmante. Prenez un entier positif
) est d’une simplicité désarmante. Prenez un entier positif ![]() . S’il est pair, divisez-le par 2. S’il est impair, multipliez-le par 3 et ajoutez 1. Recommencez. La conjecture affirme que, quel que soit le nombre de départ, vous finirez inéluctablement par tomber dans la boucle
. S’il est pair, divisez-le par 2. S’il est impair, multipliez-le par 3 et ajoutez 1. Recommencez. La conjecture affirme que, quel que soit le nombre de départ, vous finirez inéluctablement par tomber dans la boucle ![]() .
.
Un enfant de 8 ans peut comprendre l’énoncé. Mais depuis 1937, les plus grands esprits de la planète s’y cassent les dents. Paul Erdős a dit à son sujet : « Les mathématiques ne sont pas encore prêtes pour de tels problèmes. »
Et puis, il y a Idriss Aberkane.
Loin des revues à comité de lecture, loin de la validation par les pairs qui est le socle de la méthode scientifique, il a publié plusieurs « papiers » (disponible en fin d’article) affirmant avoir résolu ce problème millénaire. Il y parle de Bitcoin, de jeux vidéo, d’Hydre et de concepts qu’il semble avoir baptisés lui-même.
Alors, génie incompris ou illusionniste du vocabulaire ?
Sur ce blog, nous aimons la pensée critique, la nuance, et par-dessus tout, la vérité. Nous n’avons pas d’animosité personnelle, mais nous avons une allergie sévère au « bruit » qui se déguise en signal. J’ai donc décidé, accompagné de mon ami de confiance, de faire ce que peu ont eu le courage (ou la patience) de faire : lire le document. Vraiment.
Nous allons décortiquer sa proposition, section par section, formule par formule. Nous allons traduire son jargon « marketing » en langage mathématique standard. L’objectif n’est pas de troller pour le plaisir, mais de démontrer pourquoi l’accumulation de termes complexes ne remplace pas une démonstration rigoureuse.
Préparez-vous, nous entrons dans l’antre de l’Hydre. Et spoiler : elle n’a pas de dents.
1. L’Abstract : Le « Bingo du Bullshit »
Dès les premières lignes, le ton est donné. Un abstract scientifique a pour but de résumer une découverte. Ici, on a l’impression de lire un pitch pour une start-up blockchain qui cherche des investisseurs en 2017. Analysons ce chef-d’œuvre de la « novlangue ».
A. La salade de mots-clés : « Quiver » et « Cryptomonnaie »
« The Collatz dynamic is known to generate a complex quiver of sequences… used to generate reliable proof of work algorithms for the cryptocurrency industry. »
Traduction : « Je connais des mots compliqués. » En mathématiques, un quiver (ou carquois) est une notion précise issue de la théorie des représentations et de la théorie des catégories (un graphe orienté où les arêtes sont des morphismes). Ici, Aberkane utilise ce terme pour dire « graphe » ou « ensemble de suites ». C’est comme appeler un chat « un quadrupède félin à potentialité ronronnante ». Ça ne sert à rien, sauf à éblouir le profane. Quant à la référence aux cryptomonnaies et à la « Preuve de Travail » (Proof of Work), elle est totalement hors-sujet. La difficulté computationnelle de Collatz est connue, mais quel est le rapport avec la véracité de la conjecture ? Aucun. C’est un pur produit d’appel : « Regardez, je parle de Bitcoin, je suis moderne ! »
B. La réinvention de la roue (carrée)
« Here we establish an ad hoc equivalent of modular arithmetic… »
Attention, aveu d’échec déguisé. L’arithmétique modulaire est un outil standard, puissant et universel depuis Gauss. Dire qu’on en crée un équivalent « ad hoc » (sur mesure), c’est généralement le signe qu’on ne maîtrise pas les outils standards ou qu’on a besoin de tordre les définitions pour qu’elles collent à une démonstration bancale. En science, « ad hoc » est souvent synonyme de « bricolage pour cacher la misère ».
C. L’Hydre et l’automate
« …an automaton that is playing a Hydra game on the graph of undecided numbers… »
Ici, il invoque le « Jeu de l’Hydre » de Kirby et Paris. C’est un concept mathématique réel lié aux suites de Goodstein et à l’indécidabilité dans l’arithmétique de Peano. C’est très sexy intellectuellement. Le problème ? Collatz n’a a priori rien à voir avec une structure d’Hydre (qui nécessite une croissance très spécifique pour être tuée). Aberkane tente de plaquer une mythologie mathématique complexe sur un problème arithmétique simple pour créer une illusion de profondeur.
D. La confusion logique : ZFC vs Peano
« …proving that in ZFC the Collatz conjecture is true, before giving a promising direction to also prove it in Peano arithmetic. »
C’est ici que l’auteur marche sur des œufs sans s’en rendre compte. Il affirme prouver la conjecture dans ZFC (Théorie des Ensembles, très puissante) puis dans Peano (Arithmétique). C’est une démarche possible en soi, mais l’exécution est ici incohérente. Il invoque plus loin le « Jeu de l’Hydre » de Kirby et Paris pour justifier sa preuve. Or, ce théorème est célèbre précisément parce qu’il est indémontrable dans Peano (il nécessite une axiomatique plus forte, avec des ordinaux transfins). Aberkane se retrouve donc dans une contradiction performative : il prétend utiliser une structure (l’Hydre) dont les propriétés de finitude échappent à Peano, pour « finir » une preuve… dans Peano. Sans justifier une réduction ou un isomorphisme rigoureux (qui serait une percée majeure en logique), c’est une juxtaposition de mots-clés incompatibles.
Verdict de l’Abstract : Ce n’est pas un résumé de mathématiques, c’est un poème en prose composé de mots-clés aléatoires piochés sur Wikipédia. Il promet de résoudre un problème millénaire avec des outils « ad hoc » et des références cryptographiques. Spoiler : ça commence mal.
2. L’Introduction : Le Cocktail Mondain (et la nécromancie)
Si l’Abstract était un prospectus publicitaire, l’Introduction est une soirée VIP où l’auteur essaie désespérément de nous montrer qu’il connaît du beau linge. L’objectif ici n’est pas de poser le problème mathématique, mais de poser le statut social de l’auteur.
A. La Confédération des Affiliations Avant même de lire le texte, regardez l’en-tête. On ne nous donne pas juste un laboratoire, mais une liste de courses : Nuremberg Institute of Technology, Potsdam University, Capgemini, Unesco-Unitwin… et bien sûr, l’adresse email en @polytechnique.edu. En science, la validité d’une preuve dépend de la logique, pas du logo sur votre carte de visite. Cet étalage de badges institutionnels (mélangeant académique et consulting privé) est un argument d’autorité visuel : « Ayez confiance, je suis partout. »
B. Algues, Plumes et Codeurs Clojure
« the so-called Collatz Feather or Collatz Seaweed… popularized by Clojure programmer Oliver Caldwell »
C’est très joli, la « Plume de Collatz » (une visualisation graphique des suites). C’est poétique. Mais citer un programmeur Clojure pour introduire une preuve théorique de niveau millénaire, c’est comme citer un décorateur d’intérieur pour expliquer les fondations d’un gratte-ciel. Ça montre que l’auteur navigue sur Internet, pas dans les bibliothèques de recherche.
C. Le « Name-Dropping » d’Outre-Tombe : L’affaire Feferman
« We owe this strategy to earlier discussions with Feferman [6] on his investigations on the continuum hypothesis… »
Là, on touche au sublime (et à l’indécent). Solomon Feferman était un géant de la logique mathématique (décédé en 2016). Invoquer des « discussions » passées avec un mort pour valider une stratégie sur Collatz est une technique rhétorique douteuse. Pire encore : le lien logique. L’Hypothèse du Continu (HC) traite de la taille des infinis (y a-t-il un infini entre celui des entiers et celui des réels ?). La Conjecture de Collatz porte sur le comportement des entiers naturels. Lier les deux demande une gymnastique mentale olympique. Aberkane suggère que Collatz (entiers) peut être traité via des arbres infinis (réels). Pourquoi pas. Mais utiliser l’autorité de Feferman pour dire « c’est une bonne idée », c’est de la caution morale, pas des maths.
D. Le feu d’artifice : Go, surréels, et cardinalités…
“…origamis of n-ary trees… objects of intermediate cardinalities between ℵn and ℵn+1… Conway’s surreal numbers… game of Go.”
Attention : ici, le papier parle bien de cardinaux infinis ![]() et
et ![]() , pas d’entiers
, pas d’entiers ![]() et
et ![]() . Donc l’objection “il n’y a rien entre
. Donc l’objection “il n’y a rien entre ![]() et
et ![]() ” serait une mauvaise lecture.
” serait une mauvaise lecture.
Mais la critique de fond reste : on empile CH, arbres complets, surréels, Go… sans jamais construire un pont technique qui revient à Collatz. On a un blender conceptuel : des thèmes de logique et de théorie des jeux utilisés comme décoration, sans lemme qui relie ça à la dynamique ![]() .
.
Verdict de l’Introduction : L’auteur tente de noyer le poisson (ou l’algue) sous une avalanche de références culturelles hétéroclites. Il essaie de connecter la conjecture arithmétique la plus simple du monde à des concepts de logique avancée (HC, Surréels) sans aucune justification technique. C’est de l’esbroufe. On nous promet l’Everest, mais pour l’instant, on nous vend des cartes postales de la boutique souvenirs.
3. La Réinvention de l’Eau Tiède (Section 2)
Dans cette section, l’auteur déploie son arsenal tactique favori : la complexification artificielle. Pour impressionner la galerie, il faut que le lecteur se sente bête. Comment ? En renommant des concepts triviaux avec des symboles inédits.
A. La Découverte du Modulo 3 (Le « Scoop » des Types A, B, C)
« Definition 2.2. Type A, B and C… a number is of type A if its base 3 representation ends with digit 2… »
Arrêtez tout. Appelez Stockholm, on tient un Nobel. Idriss Aberkane vient de redécouvrir… le Modulo 3.
- Si un nombre finit par 0 en base 3, c’est qu’il est divisible par 3. (Reste 0). Il appelle ça « Type B ».
- Si un nombre finit par 1 en base 3, c’est que le reste est 1. Il appelle ça « Type C ».
- Si un nombre finit par 2 en base 3, c’est que le reste est 2. Il appelle ça « Type A ».
En mathématiques standard, on écrit simplement ![]() . C’est universel, clair et concis. Pourquoi inventer « Type A, B, C » ? C’est une technique classique de pseudocience : créer une nomenclature propriétaire pour s’approprier un concept public. C’est comme si je décidais d’appeler les nombres pairs « Type Solaire » et les impairs « Type Lunaire » pour ensuite écrire un traité sur « La dynamique Solaire-Lunaire ». Ça sonne mystique, mais c’est vide.
. C’est universel, clair et concis. Pourquoi inventer « Type A, B, C » ? C’est une technique classique de pseudocience : créer une nomenclature propriétaire pour s’approprier un concept public. C’est comme si je décidais d’appeler les nombres pairs « Type Solaire » et les impairs « Type Lunaire » pour ensuite écrire un traité sur « La dynamique Solaire-Lunaire ». Ça sonne mystique, mais c’est vide.
B. Les Opérations G, S, V : L’art du remplissage Il définit trois fonctions :
Il note ensuite triomphalement que ![]() . Vérifions ce tour de magie :
. Vérifions ce tour de magie : ![]() . Bravo. C’est de l’algèbre de niveau 4ème. Mais présenté avec des lettres capitales et des diagrammes (le fameux « Quiver » ou carquois de la Figure 1), cela donne l’illusion d’une structure algébrique profonde.
. Bravo. C’est de l’algèbre de niveau 4ème. Mais présenté avec des lettres capitales et des diagrammes (le fameux « Quiver » ou carquois de la Figure 1), cela donne l’illusion d’une structure algébrique profonde.
C. L’esbroufe de la « Règle Un » (Rule One)
“Rule One: x odd, V(x) ~ x” (où ~ signifie équivalent dans l’orbite de Collatz).
Traduction : Il affirme que ![]() et
et ![]() tombent sur le même nombre dans la suite de Collatz. Est-ce une découverte ? Non, c’est une trivialité absolue connue de tout étudiant qui a passé 10 minutes sur le problème. Démonstration (niveau lycée) : Prenons
tombent sur le même nombre dans la suite de Collatz. Est-ce une découverte ? Non, c’est une trivialité absolue connue de tout étudiant qui a passé 10 minutes sur le problème. Démonstration (niveau lycée) : Prenons ![]() . C’est un nombre impair (car
. C’est un nombre impair (car ![]() est pair). On applique Collatz (
est pair). On applique Collatz (![]() ) :
) : ![]() . C’est pair. On divise par 2 :
. C’est pair. On divise par 2 : ![]() . C’est encore pair. On divise par 2 :
. C’est encore pair. On divise par 2 : ![]() . Et voilà ! On retombe exactement sur le même résultat que si on avait appliqué Collatz à
. Et voilà ! On retombe exactement sur le même résultat que si on avait appliqué Collatz à ![]() (qui donne aussi
(qui donne aussi ![]() ). Aberkane appelle ça une « Règle Essentielle ». Les mathématiciens appellent ça « faire deux divisions par 2 pour annuler une multiplication par 4 ».
). Aberkane appelle ça une « Règle Essentielle ». Les mathématiciens appellent ça « faire deux divisions par 2 pour annuler une multiplication par 4 ».
D. L’intimidation par les indices (Règles 3, 4, 5) Regardez les formules des règles 3, 4 et 5.
![]()
C’est ce qu’on appelle de la « notation dissuasive ». L’accumulation d’indices ![]() , de puissances et de sommes sert à créer un mur de complexité. Le but n’est pas d’être lu, mais d’être craint. « Oh la la, il y a des sigmas et des puissances imbriquées, ça doit être sérieux. » En réalité, il ne fait qu’écrire de manière alambiquée des propriétés arithmétiques basiques de remontée dans l’arbre de Collatz. C’est du bruit visuel.
, de puissances et de sommes sert à créer un mur de complexité. Le but n’est pas d’être lu, mais d’être craint. « Oh la la, il y a des sigmas et des puissances imbriquées, ça doit être sérieux. » En réalité, il ne fait qu’écrire de manière alambiquée des propriétés arithmétiques basiques de remontée dans l’arbre de Collatz. C’est du bruit visuel.
Verdict de la Section 2 : Aberkane a pris des propriétés élémentaires (modulo 3, simplification par 4), les a maquillées avec du vocabulaire « ad hoc » (Types A/B/C, Quiver, Règles V/S/G) et nous vend ça comme les fondations d’une cathédrale. Pour l’instant, il a juste repeint la cabane de jardin.
4. L’Algèbre pour les Nuls (déguisée en Nobel)
Nous entrons maintenant dans le « cœur » démonstratif. Accrochez-vous, car la complexité est… totalement absente. Tout ce qui suit est du niveau collège/lycée, mais emballé dans un papier cadeau en titane.
A. La Règle Un (Rule One) : La division par 4 expliquée aux adultes Aberkane écrit :
« If a is written
then
therefore
. »
Analysons cet exploit. Il prend un nombre de la forme ![]() . Il applique la règle impaire de Collatz :
. Il applique la règle impaire de Collatz : ![]() . Il obtient
. Il obtient ![]() . Comme c’est un multiple de 4, on applique deux fois la règle paire (diviser par 2).
. Comme c’est un multiple de 4, on applique deux fois la règle paire (diviser par 2). ![]() . Conclusion : Si on part de
. Conclusion : Si on part de ![]() , on atterrit au même endroit que si on était parti de
, on atterrit au même endroit que si on était parti de ![]() et qu’on avait fait
et qu’on avait fait ![]() . C’est exact. C’est trivial. C’est connu depuis les années 50. Mais Aberkane appelle ça « Proving Rule One » comme s’il venait de démontrer le Théorème de Pythagore.
. C’est exact. C’est trivial. C’est connu depuis les années 50. Mais Aberkane appelle ça « Proving Rule One » comme s’il venait de démontrer le Théorème de Pythagore.
B. Le « Rank » et les Nombres de Mersenne (Note 2.5) Il définit le « Rank » d’un nombre comme son nombre de 1 consécutifs à la fin en binaire. Puis il découvre avec émerveillement que les nombres de Mersenne (![]() , qui s’écrivent
, qui s’écrivent ![]() en binaire) montent très haut avant de redescendre.
en binaire) montent très haut avant de redescendre.
« How many times one can add an half to an odd number +1 directly depends on its base 2 representation… »
Traduction : « Si un nombre est divisible par ![]() , on peut le diviser par 2,
, on peut le diviser par 2, ![]() fois. » Merci, Sherlock. C’est la définition de la base 2. Présenter le fonctionnement de l’arithmétique binaire comme une propriété « intrinsèque et pittoresque » de la dynamique de Collatz est une forme de remplissage textuel assez audacieuse.
fois. » Merci, Sherlock. C’est la définition de la base 2. Présenter le fonctionnement de l’arithmétique binaire comme une propriété « intrinsèque et pittoresque » de la dynamique de Collatz est une forme de remplissage textuel assez audacieuse.
C. L’inflation lexicale : « Vertical Even » et « Vertical Odd » Accrochez-vous à vos chaises.
- Il définit un nombre « Vertical Even » comme
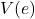 où
où  est pair. Rappel :
est pair. Rappel : 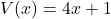 . Donc « Vertical Even » =
. Donc « Vertical Even » = 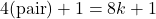 .
. - Il définit un nombre « Vertical Odd » comme
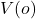 où
où  est impair. Donc « Vertical Odd » =
est impair. Donc « Vertical Odd » = 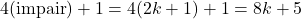 .
.
Pourquoi ne pas dire simplement « les nombres congrus à 1 modulo 8 » et « les nombres congrus à 5 modulo 8 » ? Parce que « Modulo 8 », ça fait devoir de maths. « Vertical Odd », ça fait chercheur en théorie des graphes. C’est purement cosmétique. Il renomme des classes de congruence pour donner l’illusion qu’il manipule des objets géométriques complexes.
D. Le Lemme 2.7 et l’illusion de la réduction Il utilise ces définitions pour dire :
« proving the convergence of such numbers is enough to prove the Collatz Conjecture. »
C’est la technique classique de l’illusionniste.
- On prend un problème difficile (Collatz).
- On le découpe en sous-cas triviaux (modulo 8, modulo 16, etc.).
- On montre que le sous-cas A se transforme en sous-cas B.
- On affirme : « Il suffit de prouver que le sous-cas B converge. » Le problème, c’est que prouver la convergence du sous-cas B est exactement aussi difficile que le problème original. Il n’a pas simplifié la difficulté, il l’a juste déplacée. Dire « Si je prouve que les Vertical Even de type A convergent, j’ai gagné » est vrai. Mais il ne l’a pas prouvé ! Il a juste dit que c’était une condition suffisante. C’est comme dire : « Pour guérir le cancer, il suffit de trouver un médicament qui tue toutes les cellules cancéreuses. J’ai donc réduit le problème à la recherche de ce médicament. » Certes, mais on n’est pas plus avancé.
Verdict de la Section 2 (suite) : Aberkane joue au bonneteau avec des trivialités algébriques. Il prouve que ![]() se comporte bien (ce qu’on sait), il renomme le binaire « Rank », et il baptise les modulos 8 « Vertical ». Aucune « Intelligence », aucune « Profondeur ». Juste de la réécriture syntaxique.
se comporte bien (ce qu’on sait), il renomme le binaire « Rank », et il baptise les modulos 8 « Vertical ». Aucune « Intelligence », aucune « Profondeur ». Juste de la réécriture syntaxique.
5. La Botanique de l’Absurde (Sections 2.3 & 2.4)
Si vous pensiez que renommer les modulos était le summum, attendez de voir la suite. Dans ces sections, l’auteur décide que les nombres ne sont plus seulement des entiers, mais des espèces biologiques qu’il faut classer en « Variétés ».
A. « Variety S » et « Variety V » : Bienvenue chez Truffaut
« All Variety S numbers above b are written
… » « All Variety V numbers above b are written
… »
On avait déjà les types A, B, C. Maintenant, on a les « Variétés S et V ». Traduisons ce jargon horticole : Il s’agit simplement de regarder comment se comportent certains nombres quand on remonte l’arbre de Collatz (c’est-à-dire quand on fait l’opération inverse). Il identifie des familles de nombres qui, après une multiplication par 3 et un ajout de 1, vont être divisibles par une grosse puissance de 2. C’est ce que Terry Tao (un vrai médaillé Fields qui travaille sur le sujet) appelle trivialement les « mesures de densité ». Aberkane appelle ça des « Variétés », comme s’il classait des tulipes. Ça ne change rien à la structure du problème, ça rajoute juste de l’étiquette.
B. Le Tour de Passe-Passe du ![]() (Lemma 2.9) Regardez bien cette formule qu’il balance fièrement :
(Lemma 2.9) Regardez bien cette formule qu’il balance fièrement :
![]()
Qu’est-ce que ça veut dire ? Il décrit une séquence où l’on multiplie par 3 (partie impaire) et où l’on divise par 4 (deux fois par 2). ![]() . Effectivement, si vous trouvez une suite de nombres qui subit ça indéfiniment, elle va diminuer vers 1. C’est géométrique. L’arnaque logique : Il montre que si un nombre suit ce chemin, il descend. C’est vrai. Mais la Conjecture de Syracuse, c’est de prouver que tous les nombres finissent par tomber sur un toboggan qui descend. Lui, il dit : « Regardez, j’ai trouvé des toboggans ! » On lui répond : « Oui, mais est-ce que tous les nombres montent sur le toboggan ? » Et là, il répond par un silence gêné couvert par des notations complexes. Il décrit les branches de l’arbre qui descendent, mais ne prouve absolument pas que tout l’univers des entiers est connecté à ces branches.
. Effectivement, si vous trouvez une suite de nombres qui subit ça indéfiniment, elle va diminuer vers 1. C’est géométrique. L’arnaque logique : Il montre que si un nombre suit ce chemin, il descend. C’est vrai. Mais la Conjecture de Syracuse, c’est de prouver que tous les nombres finissent par tomber sur un toboggan qui descend. Lui, il dit : « Regardez, j’ai trouvé des toboggans ! » On lui répond : « Oui, mais est-ce que tous les nombres montent sur le toboggan ? » Et là, il répond par un silence gêné couvert par des notations complexes. Il décrit les branches de l’arbre qui descendent, mais ne prouve absolument pas que tout l’univers des entiers est connecté à ces branches.
C. La Tautologie de la Figure 2 (et Section 2.4) Il nous présente de jolis graphiques (Figure 2, images fournies) avec des nœuds dorés, violets, turquoises. La légende dit : « Whenever a number is connected to 1 by a finite path… it is proven to converge to 1. »
Traduction : « Si un nombre est relié à 1, alors il va vers 1. » Merci, Monsieur de La Palice ! C’est le principe même d’un graphe connexe. Tout son papier consiste à construire l’arbre à l’envers (en partant de 1 et en remontant). Évidemment que si tu construis un arbre en partant de la racine, toutes les feuilles sont connectées à la racine ! La difficulté de la conjecture (le « Everest »), c’est de prouver qu’il n’existe aucun nombre en dehors de cet arbre (une boucle isolée ou une suite qui part vers l’infini sans jamais toucher l’arbre). Aberkane dessine l’arbre, colorie les boules, et dit : « Voyez ? Tout est connecté. » Non. Tout ce que vous avez dessiné est connecté. Ce que vous n’avez pas dessiné, c’est justement la question.
D. La « Preuve » de la Règle Cinq (Section 2.4)
« Any type A number of rank 1 can be written a = G(b)… which combined with Rule Two itself gives Rule Five. »
C’est ce qu’on appelle une « preuve par intimidation cyclique ». Il dit : « Comme on a vu avant (truc flou), et en combinant avec ceci (truc trivial), alors cela donne la Règle Cinq. » Il n’y a aucune déduction logique formelle. Il affirme que la combinaison de ses définitions crée une preuve. En réalité, il tourne en rond dans ses propres définitions : les nombres de Type A se transforment en nombres d’un autre type, qui finissent par redescendre. C’est une observation empirique (vraie pour les milliards de nombres testés par ordinateur), pas une preuve théorique pour l’infini.
Verdict des Sections 2.3 et 2.4 : Aberkane confond « décrire le chemin » et « prouver que tout le monde prend le chemin ». Il a passé beaucoup de temps à dessiner la carte des routes qui mènent à Rome, mais il n’a pas prouvé que toutes les routes mènent à Rome. Il a juste prouvé que « les routes qui mènent à Rome… mènent à Rome ».
5. L’Automate en Plaqué Or (Section 3)
Si vous avez survécu aux « plumes », aux « algues » et aux « variétés », bienvenue dans le monde merveilleux de « l’Automate Doré ». Ici, l’auteur abandonne définitivement la rigueur pour entrer dans le mysticisme marketing.
A. « Golden Arithmetic » et l’extension épistémologique
« Our purpose is to develop an ad hoc unary algebra… which we intend as an epistemological extension of modular arithmetic… »
Arrêtons-nous une seconde. L’épistémologie est l’étude critique des sciences et de la connaissance. L’arithmétique modulaire est une méthode de calcul sur les restes. Dire qu’on fait une « extension épistémologique » de l’arithmétique, ça ne veut absolument rien dire. C’est du « bullshit » (au sens technique défini par le philosophe Harry Frankfurt) : des mots assemblés pour impressionner sans souci de vérité. Pourquoi « Golden » ? Y a-t-il un rapport avec le Nombre d’Or (![]() ) ? Absolument aucun. C’est juste que « Golden », ça fait riche. Ça brille.
) ? Absolument aucun. C’est juste que « Golden », ça fait riche. Ça brille.
B. La Tortue Logo et la Composition de Fonctions
« just like in turtle graphics. For example VGS3 means 3 ◦ S ◦ G ◦ V »
Il redécouvre ici la composition de fonctions. En mathématiques, quand on applique ![]() puis
puis ![]() , on écrit
, on écrit ![]() . C’est standard depuis des siècles. Lui, il a besoin de citer « Turtle Graphics » (le langage Logo pour les enfants dans les années 80) pour expliquer ça. C’est infantilisant. L’objet qu’il décrit (des mots formés par des lettres d’opérateurs) est un objet classique en théorie des groupes et des monoïdes. Mais au lieu de dire « Soit le monoïde engendré par… », il nous parle de tortues.
. C’est standard depuis des siècles. Lui, il a besoin de citer « Turtle Graphics » (le langage Logo pour les enfants dans les années 80) pour expliquer ça. C’est infantilisant. L’objet qu’il décrit (des mots formés par des lettres d’opérateurs) est un objet classique en théorie des groupes et des monoïdes. Mais au lieu de dire « Soit le monoïde engendré par… », il nous parle de tortues.
C. L’Arnaque de la « Conjecture 3.1 » C’est le point crucial de l’escroquerie intellectuelle de ce papier. Il observe que son automate (qui ne fait que remonter l’arbre à l’envers en partant de 1) trouve beaucoup de nombres. Il voit que 15 mène à 31, que 7 mène à 127. Et là, il pose la Conjecture 3.1 :
« Suppose all odd numbers up to
are proven to converge… then the Golden Automaton finitely proves the convergence of those up to
«
Traduction : « Si on suppose que ça marche jusqu’à un certain point, alors je parie que mon automate prouve que ça marche un peu plus loin. » Ceci n’est pas une preuve. C’est une induction non démontrée. Pour prouver Syracuse, il faut prouver que cette induction est vraie tout le temps. Il ne le fait pas ! Il dit juste « Regardez, ça a marché pour 15 et 31, donc ça doit marcher tout le temps ». Remplacer la Conjecture de Collatz par une « Conjecture de l’Automate Doré » ne résout rien. C’est déplacer le problème d’une poche à l’autre en espérant que personne ne remarque le tour de passe-passe.
D. L’Invocation finale de ZFC
« why it can be proven they can reach any number in 2N+1 in ZFC. »
Et bim, le retour de ZFC (Zermelo-Fraenkel + Axiome du Choix). Il affirme sans trembler qu’on peut prouver dans ZFC que son automate atteint tous les nombres impairs. C’est littéralement l’énoncé de la conjecture de Syracuse (à l’envers : tout nombre impair atteint 1). Donc il conclut sa section en disant : « Dans la prochaine section, je vais vous montrer pourquoi on peut prouver que la conjecture est vraie. » C’est une pétition de principe. Il affirme ce qu’il est censé démontrer.
Verdict de la Section 3 : L’auteur a construit un algorithme qui remonte l’arbre de Collatz (ce que n’importe quel programmeur sait faire en 5 lignes de Python). Il lui a donné un nom sacré (« Golden Automaton »), a maquillé la composition de fonctions en « Turtle Graphics », et a remplacé la preuve manquante par une nouvelle conjecture qui dit « Croyez-moi, ça continue ». C’est du vent doré à la feuille.
6. L’Album de Coloriage et le Retour de l’Hydre (Section 3.2)
Après nous avoir vendu un « Automate Doré », l’auteur passe à la phase « démonstration par l’image ». Le but de cette section est, selon ses propres termes, d’identifier des « propriétés fondamentales prouvables » en dessinant l’arbre en plus grand.
A. La Preuve par le « Zoom Dézoom »
« The purpose… is to identify provable fundamental properties… by scaling it up »
Regardez les Figures 3, 4, 5 et 6. Que voyons-nous ? L’arbre de Collatz inversé (les nombres qui mènent à 1) pour les nombres inférieurs à 32, puis 64, puis 128, puis 256. C’est tout. Il a lancé son script Python (ou celui du programmeur Clojure cité en intro) et a fait des captures d’écran. En science, montrer que votre algorithme marche pour ![]() ne prouve rien sur l’infini. Rappelons que la conjecture a été vérifiée par ordinateur jusqu’à
ne prouve rien sur l’infini. Rappelons que la conjecture a été vérifiée par ordinateur jusqu’à ![]() (environ
(environ ![]() ). Aberkane nous montre des graphes jusqu’à 256 et appelle ça un « Scale-up ». C’est comme vouloir prouver que l’océan est infini en nous montrant une photo de sa baignoire, puis de sa piscine.
). Aberkane nous montre des graphes jusqu’à 256 et appelle ça un « Scale-up ». C’est comme vouloir prouver que l’océan est infini en nous montrant une photo de sa baignoire, puis de sa piscine.
B. Le Mythe de l’Hydre (Le « Godwin Point » Mathématique)
« proving the convergence… is always isomorphic to a Hydra Game. » « elements of
… precisely form the heads in the Hydra Game. »
Attention, danger. Ici, il sort l’artillerie lourde du jargon pour noyer le poisson. Le « Jeu de l’Hydre » de Kirby et Paris est un résultat célèbre de logique mathématique. Il implique des suites de Goodstein et des ordinaux (![]() ). Sa particularité ? La preuve que l’Hydre meurt toujours est impossible dans l’arithmétique de Peano seule. Aberkane affirme, sans la moindre preuve formelle dans cette section, que Collatz est isomorphe (structurellement identique) à ce jeu. C’est une affirmation extraordinaire qui demande une preuve extraordinaire. Où est-elle ? Il dit : « as we demonstrate in the next section ». (Le fameux « demain, on rase gratis »). Pour l’instant, il se contente de dire : « Regardez, j’ai colorié les nombres de forme
). Sa particularité ? La preuve que l’Hydre meurt toujours est impossible dans l’arithmétique de Peano seule. Aberkane affirme, sans la moindre preuve formelle dans cette section, que Collatz est isomorphe (structurellement identique) à ce jeu. C’est une affirmation extraordinaire qui demande une preuve extraordinaire. Où est-elle ? Il dit : « as we demonstrate in the next section ». (Le fameux « demain, on rase gratis »). Pour l’instant, il se contente de dire : « Regardez, j’ai colorié les nombres de forme ![]() en rouge, et je dis que ce sont les têtes de l’Hydre. » Pourquoi
en rouge, et je dis que ce sont les têtes de l’Hydre. » Pourquoi ![]() ? (Soit
? (Soit ![]() ). Parce que ce sont des nombres qui montent vite ? Peut-être. Mais coller l’étiquette « Tête d’Hydre » sur une classe de congruence ne crée pas un lien magique avec les théorèmes de Kirby et Paris. C’est de l’association d’idées, pas des mathématiques.
). Parce que ce sont des nombres qui montent vite ? Peut-être. Mais coller l’étiquette « Tête d’Hydre » sur une classe de congruence ne crée pas un lien magique avec les théorèmes de Kirby et Paris. C’est de l’association d’idées, pas des mathématiques.
C. L’illusion de la complétude Les schémas sont jolis (Figures 4, 5, 6). Ils montrent que l’arbre est touffu. Mais le problème de Collatz, c’est justement de savoir s’il existe des nombres qui ne sont pas dans cet arbre (des nombres qui ne mènent jamais à 1). En dessinant l’arbre des nombres qui mènent à 1, Aberkane ne montre que les réussites. Il ne prouve pas l’absence d’échecs. C’est le biais du survivant appliqué aux mathématiques. Il dit : « Regardez, mon automate trouve plein de nombres ! » On répond : « Oui, mais est-ce qu’il les trouve tous ? » Et pour répondre à ça, il nous renvoie à… ZFC et l’Hydre. La boucle de la circularité est bouclée.
Verdict de la Section 3.2 : C’est une galerie d’art génératif. L’auteur confond « visualisation de données » et « démonstration ». Il plaque le mot « Hydre » sur son coloriage pour donner une aura de mystère indécidable à son travail, préparant le terrain pour la section suivante qui promet d’être le bouquet final du non-sens.
7. Le Cosplay Mathématique : L’Hydre en polystyrène (Section 4 & 4.1)
Nous arrivons au cœur du réacteur. C’est ici que l’auteur prétend plier l’histoire des mathématiques. Il affirme avoir prouvé la conjecture dans ZFC (théorie des ensembles) et dans Peano. Spoiler : Il vient de commettre un suicide logique en direct.
A. La Contradiction Fondamentale (Le crash ZFC vs Peano) Dès le titre, on rit (jaune).
« We prove that Collatz conjecture holds in ZFC… and we prove that Collatz conjecture also holds in the Peano Arithmetic. »
Ensuite, il invoque le théorème de l’Hydre de Kirby et Paris [9]. Le problème : Le théorème de l’Hydre est célèbre précisément parce qu’il est vrai, mais improuvable dans l’arithmétique de Peano (il nécessite des ordinaux jusqu’à ![]() ). Si Aberkane affirme que :
). Si Aberkane affirme que :
- Collatz est équivalent (isomorphe) au jeu de l’Hydre.
- L’Hydre nécessite plus que Peano pour être prouvée. Alors il ne peut pas prétendre prouver Collatz DANS Peano. C’est l’un ou l’autre. Soit sa preuve dans Peano est fausse, soit son analogie avec l’Hydre est fausse. En affirmant les deux simultanément, il montre qu’il ne comprend pas la portée du théorème qu’il cite. C’est du « name-dropping » qui se retourne contre son auteur.
De plus, il affirme que l’Axiome du Choix (AC) est nécessaire pour démontrer qu’aucune Hydre ne survit. C’est faux. Le théorème de Kirby-Paris repose sur l’induction transfinie jusqu’à l’ordinal ![]() , pas sur l’Axiome du Choix. Invoquer l’Axiome du Choix ici est suspect : cela suggère que l’auteur confond la complexité logique (arithmétique du second ordre) avec les fondements ensemblistes. C’est comme dire qu’on a besoin de la physique quantique pour expliquer comment cuire des pâtes.
, pas sur l’Axiome du Choix. Invoquer l’Axiome du Choix ici est suspect : cela suggère que l’auteur confond la complexité logique (arithmétique du second ordre) avec les fondements ensemblistes. C’est comme dire qu’on a besoin de la physique quantique pour expliquer comment cuire des pâtes.
B. Les Nombres « Ag » : La numérologie 2.0
« A type A number that is vertical even is called an Ag… The set of Ag numbers is
«
Il définit les « têtes de l’Hydre » comme étant les nombres de la forme ![]() (ex: 17, 41, 65…). Pourquoi ? Parce que ça l’arrange. Une « Hydre » mathématique est un arbre enraciné (une structure topologique). Ici, ses « Ag » sont juste des entiers dans une progression arithmétique. Affirmer « Ces nombres sont les têtes de l’Hydre » sans construire la structure d’arbre rigoureuse qui relie ces nombres entre eux via des arêtes définies, c’est comme dire « Ces cailloux sont des pions d’échecs » sans dessiner l’échiquier ni donner les règles de déplacement.
(ex: 17, 41, 65…). Pourquoi ? Parce que ça l’arrange. Une « Hydre » mathématique est un arbre enraciné (une structure topologique). Ici, ses « Ag » sont juste des entiers dans une progression arithmétique. Affirmer « Ces nombres sont les têtes de l’Hydre » sans construire la structure d’arbre rigoureuse qui relie ces nombres entre eux via des arêtes définies, c’est comme dire « Ces cailloux sont des pions d’échecs » sans dessiner l’échiquier ni donner les règles de déplacement.
C. La « Preuve » par l’Esquive (Hand-waving) Attention, voici la phrase la plus magique du papier :
« It could be demonstrated that the Golden Automaton is playing an even simpler game… but as this is needless for the final proof we can now simply demonstrate… »
Traduction : « Je pourrais le prouver, mais j’ai la flemme, donc je vais juste dire que c’est vrai. » En mathématiques, la phrase « It could be demonstrated » est interdite si la démonstration ne suit pas. Il affirme que son automate « coupe des têtes » (réduit les nombres Ag). Mais le Jeu de l’Hydre a une règle de croissance terrifiante : quand on coupe une tête, l’Hydre repousse ![]() copies du sous-arbre. Où est l’analogie arithmétique ici ? Aberkane écrit : « How do they grow? … Let b be of type B… there are numbers smaller than… » Il liste des inégalités floues. Il ne montre jamais que la structure arithmétique de Collatz reproduit la duplication exponentielle des branches de l’Hydre de Kirby-Paris. Il plaque le mot « Hydre » sur une simple descente arithmétique.
copies du sous-arbre. Où est l’analogie arithmétique ici ? Aberkane écrit : « How do they grow? … Let b be of type B… there are numbers smaller than… » Il liste des inégalités floues. Il ne montre jamais que la structure arithmétique de Collatz reproduit la duplication exponentielle des branches de l’Hydre de Kirby-Paris. Il plaque le mot « Hydre » sur une simple descente arithmétique.
D. L’Isomorphisme Fantôme Pour utiliser le théorème de Kirby-Paris, il faut prouver un isomorphisme formel :
![]()
Il faut associer à chaque entier un ordinal ![]() et montrer que chaque étape de Collatz fait strictement décroître cet ordinal. Aberkane ne définit aucun ordinal. Il ne définit aucune bijection structurelle. Il dit juste : « Mon automate atteint des nombres, l’Hydre a des têtes, donc mon automate joue à l’Hydre. » C’est du raisonnement analogique de niveau poésie, pas de la théorie de la démonstration.
et montrer que chaque étape de Collatz fait strictement décroître cet ordinal. Aberkane ne définit aucun ordinal. Il ne définit aucune bijection structurelle. Il dit juste : « Mon automate atteint des nombres, l’Hydre a des têtes, donc mon automate joue à l’Hydre. » C’est du raisonnement analogique de niveau poésie, pas de la théorie de la démonstration.
Verdict de la Section 4.1 : C’est un château de cartes bâti sur un marécage. L’auteur invoque un théorème puissant (l’Hydre) qu’il contredit lui-même en prétendant prouver le résultat dans Peano. Il n’y a aucune preuve, juste une collection d’affirmations péremptoires (« Ag numbers are heads ») qui tentent de transformer une suite de nombres en monstre mythologique par la seule force de la volonté.
8. Le Coloriage Magique et la Preuve par Excel (Section 4.2)
Si la section précédente était une insulte à la logique, celle-ci est une insulte à la rigueur expérimentale. L’auteur se demande : « Can Peano Arithmetic also prove the Collatz conjecture? » Sa réponse ? « Regardez mes jolis points bleus et jaunes. »
A. Le « Jeu de la Vie » du pauvre
« a zero-player game… significantly simpler than John Conway’s Game of Life »
Il définit un automate cellulaire avec trois couleurs :
- Gold : Nombre atteint, pas encore traité.
- Blue : Nombre traité.
- Black : Nombre pas encore atteint.
En informatique, on appelle ça… un algorithme de parcours en largeur (BFS). C’est littéralement le premier algorithme qu’on apprend pour explorer un graphe. Aberkane rebaptise « Open Set » en « Gold » et « Closed Set » en « Blue », ajoute une référence à Conway pour la « street cred », et prétend avoir inventé un « Jeu ».
Regardez cette complexité inouïe : il colorie les cases. C’est du niveau « Paint », pas « Peano ».
B. L’Hécatonchire : Le Name-Dropping Mythologique (Encore)
« a much simpler game one could call Hecatonchire v. Hydra game »
Il ne pouvait pas s’en empêcher. Après l’Hydre, voici les Hécatonchires (les géants aux cent bras). Ça n’apporte rien à la démonstration. C’est juste pour dire : « Mon algorithme est super fort, il a cent bras. » En maths, on appelle ça une croissance exponentielle du front de recherche. Pas besoin d’invoquer la mythologie grecque pour décrire une boucle for.
C. La « Science de la Data » (Data Science) à la rescousse du vide C’est ici que l’effondrement intellectuel est total. Il définit une « Dépense Computationnelle » (Computational Expense) : combien de nombres il doit « colorier » pour finir une rangée de l’arbre binaire. Il trace ensuite ces données sur un graphique.
À gauche : échelle linéaire. À droite : échelle logarithmique.
Il observe que la courbe ressemble à une droite sur l’échelle logarithmique (Figure 14). Sa conclusion implicite ? « Ça a l’air de faire une ligne, donc c’est prouvé. » C’est une hérésie.
- L’échelle ridicule : Il s’arrête à la « Row 12 » (environ 4096). La conjecture a été vérifiée par de vrais mathématiciens jusqu’à
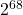 . Ses graphiques sont microscopiques comparés à ce qu’on sait déjà.
. Ses graphiques sont microscopiques comparés à ce qu’on sait déjà. - L’extrapolation abusive : En mathématiques, on ne prouve pas un théorème en disant « Regardez, la courbe Excel est jolie ». La distribution des nombres premiers a aussi l’air régulière de loin, et pourtant elle cache des chaos profonds (les zéros de Riemann). Confondre « tendance statistique sur 12 points » et « preuve formelle dans l’arithmétique de Peano » est une faute éliminatoire.
D. Les graphiques de remplissage Il nous inonde de graphiques de points (Figures 10, 11, 12, 13).
Que montrent-ils ? Que son algorithme remplit les trous. C’est tautologique : son algorithme est conçu pour remplir les trous. Montrer que « ça marche pour les petits nombres » n’est pas une stratégie de preuve. C’est une vérification. Et une vérification très, très lente par rapport à l’état de l’art.
Verdict de la Section 4.2 : L’auteur confond comportement probabiliste et certitude logique. Terras (1976) avait déjà prouvé que « presque tous » les nombres ont un temps d’arrêt fini (ils finissent par redescendre en dessous de leur point de départ). C’est un résultat de densité, pas de convergence totale. Aberkane refait ce genre de calculs en moins rigoureux, avec des métaphores de biologie, et croit avoir prouvé l’inexistence de contre-exemples par la seule force d’une moyenne légèrement supérieure à la croissance du graphe (grâce à son epsilon magique). C’est un échec complet.
9. La Guerre des Boutons et le « Fudge Factor » (Fin de la Section 4.2)
L’auteur conclut son papier en proposant deux stratégies pour « finaliser » la preuve. Spoiler : aucune des deux n’est une preuve.
A. Stratégie 1 : La Preuve par « Ça a l’air droit »
« single out the linear behavior we expose in Figure 14 as a provable property »
Il revient à son graphique Excel. Il dit : « La courbe a l’air linéaire, donc on doit pouvoir prouver qu’elle l’est. » C’est le degré zéro du raisonnement. En théorie du chaos et des systèmes dynamiques, des comportements semblent linéaires pendant très longtemps avant de bifurquer brutalement. Dire « utilisons la preuve automatique pour confirmer que mon dessin est une loi universelle » est une prière, pas une stratégie.
B. Stratégie 2 : La Démographie des Nombres (L’attaque des Clones) Il bascule dans une métaphore biologique/virale confuse. Il parle de « Taux de reproduction » (![]() ) des points dorés (les nombres prouvés) contre les points noirs (les inconnus). L’idée : Si les nombres prouvés se reproduisent plus vite que les nombres inconnus, ils vont finir par « gagner » et envahir tout l’arbre. L’erreur fatale : Le problème de Collatz ne se résout pas par des moyennes. Même si le taux de reproduction moyen est favorable, cela n’empêche pas l’existence d’une lignée isolée (une branche rebelle) qui résiste et part à l’infini. En mathématiques, la moyenne ne tue pas l’exception.
) des points dorés (les nombres prouvés) contre les points noirs (les inconnus). L’idée : Si les nombres prouvés se reproduisent plus vite que les nombres inconnus, ils vont finir par « gagner » et envahir tout l’arbre. L’erreur fatale : Le problème de Collatz ne se résout pas par des moyennes. Même si le taux de reproduction moyen est favorable, cela n’empêche pas l’existence d’une lignée isolée (une branche rebelle) qui résiste et part à l’infini. En mathématiques, la moyenne ne tue pas l’exception.
C. Le Désastre Arithmétique du 3,5 Accroche-toi bien. Il fait ses calculs (basés sur des hypothèses probabilistes fragiles).
- Taux de reproduction des « Black dots » (le méchant chaos) : converge vers
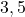 .
. - Taux de reproduction des « Gold dots » (la gentille preuve) :
- Type B :
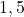
- Type C :
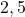
- Type A : converge vers
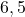 (via une série infinie). Il fait la moyenne des trois types :
(via une série infinie). Il fait la moyenne des trois types : 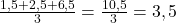 .
.
- Type B :
Catastrophe ! Il arrive à une égalité parfaite : ![]() contre
contre ![]() . Dans un vrai papier de recherche, ce serait le moment où l’auteur admet : « Mince, c’est un match nul, je ne peux pas conclure à la domination stricte. »
. Dans un vrai papier de recherche, ce serait le moment où l’auteur admet : « Mince, c’est un match nul, je ne peux pas conclure à la domination stricte. »
D. Le Coup de l’Epsilon (La triche ultime) Mais Aberkane ne s’arrête pas là. Face à cette égalité qui ruine sa démonstration, il écrit cette phrase hallucinante :
« Since we did not count the offspring of C and B type numbers… we can prove the average birthrate… tends to equal
with
, which finishes the Peano-arithmetical proof. »
Traduction : « J’ai trouvé une égalité, mais comme je suis sûr d’avoir oublié de compter des trucs favorables, je rajoute un petit ![]() positif, et hop, j’ai gagné. » C’est ce qu’on appelle en argot scientifique un « Fudge Factor » : on bidouille le résultat pour qu’il colle à la conclusion désirée. Affirmer « il y a surement un reste positif quelque part » sans le calculer, c’est de la foi, pas des maths. Et conclure par « which finishes the Peano-arithmetical proof » est d’une arrogance stupéfiante. Il n’a rien fini du tout. Il a fait une moyenne probabiliste, a trouvé une égalité, et a ajouté
positif, et hop, j’ai gagné. » C’est ce qu’on appelle en argot scientifique un « Fudge Factor » : on bidouille le résultat pour qu’il colle à la conclusion désirée. Affirmer « il y a surement un reste positif quelque part » sans le calculer, c’est de la foi, pas des maths. Et conclure par « which finishes the Peano-arithmetical proof » est d’une arrogance stupéfiante. Il n’a rien fini du tout. Il a fait une moyenne probabiliste, a trouvé une égalité, et a ajouté ![]() à la main pour déclarer victoire.
à la main pour déclarer victoire.
10. L’Apothéose de l’Ego et le Cimetière des Références (Section 5 & Biblio)
On finit souvent un papier par des remerciements humbles. Ici, c’est une distribution de médailles en chocolat.
A. La 3ème personne du singulier : « I. Aberkane created… »
« I. Aberkane created the framework… identified and demonstrated the five rules… predicted they would be isomorphic to a Hydra game… allowing for a final demonstration… »
C’est fascinant. Dans la section « Attribution », Aberkane écrit sa propre hagiographie. Il s’attribue tout le mérite conceptuel (« created », « demonstrated », « predicted », « final demonstration »). Ses co-auteurs, Sultanow et Rahn ? Ils ont « codé » et « fait tourner les simulations ». En gros, ce sont ses exécuteurs techniques. Lui est le cerveau, eux sont les mains. Cette hiérarchisation explicite est rare et assez mal vue en science collaborative, surtout quand le « cerveau » n’a rien prouvé.
B. Le « Name-Dropping » Nécrophile (Dedication)
« The authors dedicate this work to the memory of John Horton Conway… Solomon Feferman… and Alan T. Waterman Jr. »
Dédier ce papier à John Conway est d’une ironie cruelle. Conway est le génie des automates cellulaires (Jeu de la Vie) et des Nombres Surréels. Aberkane a pris le « Jeu de la Vie », l’a vidé de sa substance pour en faire un coloriage binaire, et ose dédier le résultat au maître. C’est comme dédier une chanson de Jul à Mozart. Citer Feferman (logicien rigoureux) alors qu’on vient de violer la logique entre ZFC et Peano est tout aussi audacieux.
C. La Bibliographie : Le Vide intersidéral Regardons les sources censées soutenir la « découverte du siècle » :
- [2] et [3] : Aberkane cite… Aberkane (sur HAL, une archive ouverte sans comité de lecture). L’auto-citation est la brique de base de la bulle spéculative académique.
- [4] et [5] : Sultanow (le co-auteur) cite Sultanow.
- [7] Donald Knuth, « Surreal Numbers » : C’est un livre de vulgarisation romancé (une fiction mathématique), pas un traité de recherche fondamentale utilisé pour des preuves de ce niveau.
- [1] Bocart : Un papier sur la crypto et la « Proof of Work ». C’est la seule justification pour avoir parlé de Blockchain au début. Ça n’a rien à voir avec la preuve de Collatz.
Conclusion de l’analyse : Il n’y a aucune référence à des travaux récents sérieux sur Collatz (comme ceux de Tao ou Lagarias). L’auteur vit dans une bulle fermée où il cite ses amis, des morts illustres, et des concepts qu’il a lui-même inventés.
Conclusion : L’Autopsie d’une Illusion
Alors, Idriss Aberkane a-t-il résolu la Conjecture de Syracuse ?
La réponse est un non catégorique, définitif et sans appel.
Ce document n’est pas une avancée mathématique. C’est un cas d’école de mimétisme scientifique (ou « Cargo Cult Science » comme dirait Feynman). Il a l’apparence de la science (les graphiques, le LaTeX, les références, le jargon), mais il n’en a ni la substance, ni la rigueur.
En résumé, voici la recette de ce « papier » :
- Prenez des concepts triviaux (modulo 3, base 2, parcours en largeur).
- Renommez-les avec du vocabulaire grandiloquent (« Golden Automaton », « Varieties », « Hecatonchire »).
- Invoquez des concepts complexes hors-sujet pour intimider le lecteur (Hydre, ZFC, Blockchain, Bitcoin).
- Remplacez la preuve logique manquante par des graphiques générés sur Excel et une « intuition » probabiliste (
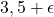 ).
). - Auto-attribuez-vous le génie de la découverte et dédiez le tout à des mathématiciens décédés qui ne peuvent pas protester.
La Conjecture de Syracuse résiste aux plus grands esprits depuis près d’un siècle. Prétendre l’avoir vaincue en 19 pages aérées, sans utiliser les outils modernes de la théorie analytique des nombres, relève au mieux d’une naïveté touchante, au pire d’une vanité dévorante.
L’Hydre de Syracuse a encore toutes ses têtes. Ce papier, lui, n’a ni queue ni tête.
Pour télécharger son papier:
Sources
Base de travail
- https://pourton.info/wp-content/uploads/2025/12/2101.09719v1.pdf
- ArXiv published my paper under incorrect subject area – Academia Stack Exchange, consulté le décembre 18, 2025, https://academia.stackexchange.com/questions/223903/arxiv-published-my-paper-under-incorrect-subject-area
- Mathematics paper in arXiv general math section – Academia Stack Exchange, consulté le décembre 18, 2025, https://academia.stackexchange.com/questions/195546/mathematics-paper-in-arxiv-general-math-section
- Lecture et analyse des articles d’Idriss Aberkane sur la conjecture de Syracuse, consulté le décembre 18, 2025, https://www.maths-et-physique.net/aberkane-syracuse.html
- 935 PDFs | Review articles in COLLATZ CONJECTURE – ResearchGate, consulté le décembre 18, 2025, https://www.researchgate.net/topic/Collatz-Conjecture/publications/6
- An Algorithm for Linearizing the Collatz Convergence – ResearchGate, consulté le décembre 18, 2025, https://www.researchgate.net/publication/353776681_An_Algorithm_for_Linearizing_the_Collatz_Convergence
- On the Restricted Ordinal Theorem – ResearchGate, consulté le décembre 18, 2025, https://www.researchgate.net/publication/38374253_On_the_Restricted_Ordinal_Theorem
- Idriss Aberkane – Wikipedia, consulté le décembre 18, 2025, https://en.wikipedia.org/wiki/Idriss_Aberkane
- Collatz Conjecture and Natural Numbers – ResearchGate, consulté le décembre 18, 2025, https://www.researchgate.net/topic/Collatz-Conjecture~Natural-Numbers/publications
- (PDF) Collatz convergence is a Hydra game – ResearchGate, consulté le décembre 18, 2025, https://www.researchgate.net/publication/348757172_Collatz_convergence_is_a_Hydra_game
- An Algorithm for Linearizing the Collatz Convergence – MDPI, consulté le décembre 18, 2025, https://www.mdpi.com/2227-7390/9/16/1898
- Collatz Sequences in the Light of Graph Theory – Semantic Scholar, consulté le décembre 18, 2025, https://www.semanticscholar.org/paper/Collatz-Sequences-in-the-Light-of-Graph-Theory-Sultanow-Koch/a0340f8ac5ad44208ccbdc3e329a3c846a2c4955
- Symbolic Collapse Geometry as the Underlying Field Law of Zeta Instability and Prime Gap Dynamics – Preprints.org, consulté le décembre 18, 2025, https://www.preprints.org/manuscript/202504.0223
- Pourquoi je revendique la résolution de Syracuse !? | IDRISS ABERKANE – YouTube, consulté le décembre 18, 2025, https://www.youtube.com/watch?v=ND9zQSo0cgQ
- idriss aberkane – Google Scholar, consulté le décembre 18, 2025, https://scholar.google.com/citations?user=Rq-TE30AAAAJ&hl=fr
 Pourton.info
Pourton.info 



