Que ce soit pour envoyer un message à votre crush, commander une pizza en ligne, ou cacher vos données bancaires, vos secrets numériques reposent sur une seule et unique chose : les maths. Mais pas n’importe lesquelles ! Derrière chaque mot de passe sécurisé et chaque connexion chiffrée, il y a une symphonie de nombres premiers, de puissances modulaires et de fonctions mystérieuses qu’on appelle « à sens unique ».
Dans cet article, on va explorer ces concepts qui transforment les équations en remparts, et voir comment les mathématiques modernes protègent vos données dans un monde où les cyberattaques sont plus fréquentes que les spams dans votre boîte mail. Du logarithme discret à la cryptographie post-quantique, en passant par Sophie Germain (oui, elle aussi), préparez-vous à un voyage où les chiffres sont vos meilleurs alliés.
Et ne vous inquiétez pas, même si ça devient technique, on garde un ton léger (avec quelques blagues au passage, promis). Alors, installez-vous confortablement, et laissez les maths vous raconter une histoire… celle de vos secrets numériques.
Chapitre 1 : Pourquoi cacher un secret, c’est un problème de maths ?

Il était une fois… un monde numérique où tout le monde voulait garder ses petits secrets : mots de passe, messages d’amour, photos de chats, et même le plan diabolique pour conquérir la cafétéria. Mais protéger un secret, c’est bien plus compliqué qu’on ne le pense. Et c’est là que les maths entrent en jeu.
Quand on parle de cacher un secret, le but est simple :
- Vous (l’émetteur du message) devez être capable de transformer facilement votre secret en quelque chose d’indéchiffrable.
- Le destinataire (votre complice) doit pouvoir faire l’opération inverse… mais pas les autres (coucou, les hackers !).
La clé de tout ça ? Trouver une manière de coder un secret pour qu’il soit facile à « écrire » mais quasi-impossible à lire sans la bonne méthode. C’est ce qu’on appelle en cryptographie une fonction à sens unique. Dit autrement : facile à faire, très dur à défaire.
Petite analogie pour vous chauffer
Imaginez que vous avez une boîte avec un cadenas très spécial. Vous pouvez facilement la fermer en tournant une clé (facile à faire), mais pour rouvrir le cadenas, il faudrait des millions d’années de tentatives (difficile à défaire). Les maths sont le cadenas de votre secret, et votre clé, c’est ce qu’on va appeler le « secret ![]() « .
« .
Mathématisation du secret
Prenons les choses sérieusement. Supposons que votre secret soit un nombre ![]() . En cryptographie, on va transformer ce nombre
. En cryptographie, on va transformer ce nombre ![]() en un autre nombre
en un autre nombre ![]() , à l’aide d’une fonction
, à l’aide d’une fonction ![]() . Ainsi :
. Ainsi :
![]()
L’idée ici, c’est que même si quelqu’un (disons un espion à la NSA ou un étudiant malicieux) voit ![]() , il ne puisse pas retrouver
, il ne puisse pas retrouver ![]() . La fonction
. La fonction ![]() doit donc être :
doit donc être :
- Facile à calculer : Vous ne voulez pas passer des siècles à crypter vos données.
- Difficile à inverser : Même en connaissant
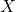 ,
, 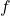 , et toutes les astuces,
, et toutes les astuces, 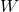 doit rester introuvable.
doit rester introuvable.
Mais alors, comment choisir ![]() ? Là, on fait appel à l’arithmétique modulaire et à des concepts élégants comme l’exponentiation modulaire (qu’on verra bientôt). Spoiler : ça implique des nombres premiers, des résidus et des tours de passe-passe mathématiques.
? Là, on fait appel à l’arithmétique modulaire et à des concepts élégants comme l’exponentiation modulaire (qu’on verra bientôt). Spoiler : ça implique des nombres premiers, des résidus et des tours de passe-passe mathématiques.
Mais pourquoi des maths ?
Les maths offrent un terrain de jeu parfait : elles sont logiques, précises, et, surtout, implacables. Les lois qui régissent nos équations cryptographiques ne font pas d’exception. Pas d’astuces, pas de raccourcis magiques. Tout repose sur la solidité des algorithmes et sur des problèmes mathématiques « difficiles » (on y reviendra).
C’est pour ça que cacher un secret est avant tout un problème mathématique :
- On utilise des nombres pour coder l’information.
- On choisit des opérations complexes pour protéger les secrets.
- Et surtout, on mise sur des concepts qui résistent même aux ordinateurs les plus rapides.
Alors, prêts à plonger dans ce monde où votre sécurité repose sur des équations ? Passons à la suite !
Chapitre 2 : La fonction à sens unique : votre secret, une aiguille dans une botte de chiffres
Imaginez ceci : vous jetez une pierre dans un lac et observez les ondulations sur l’eau. Facile, non ? Mais maintenant, essayez de deviner où se trouve exactement la pierre en ne regardant que les ondulations. Bonne chance. C’est ce qu’on appelle un problème « facile à faire mais difficile à défaire », et en cryptographie, c’est précisément ce que l’on cherche à créer.
Une fonction à sens unique, c’est l’équivalent mathématique de cette pierre dans le lac. Elle transforme un secret (appelons-le ![]() ) en un résultat visible (appelons-le
) en un résultat visible (appelons-le ![]() ), mais sans laisser de piste claire pour remonter à
), mais sans laisser de piste claire pour remonter à ![]() . Notamment, les fonctions à sens unique doivent avoir deux propriétés fondamentales :
. Notamment, les fonctions à sens unique doivent avoir deux propriétés fondamentales :
- Faciles à calculer : On doit pouvoir passer de
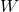 à
à 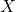 en un claquement de doigts (ou presque).
en un claquement de doigts (ou presque). - Difficiles à inverser : Même en connaissant
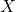 , il est pratiquement impossible de retrouver
, il est pratiquement impossible de retrouver 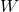 sans essayer toutes les valeurs possibles… et encore.
sans essayer toutes les valeurs possibles… et encore.
Exemple classique : la multiplication
Prenons un exemple simple. Si je vous dis que deux nombres ![]() et
et ![]() ont été multipliés pour donner un résultat
ont été multipliés pour donner un résultat ![]() , vous pouvez facilement calculer :
, vous pouvez facilement calculer :
![]()
Mais si je vous donne ![]() et vous demande de retrouver
et vous demande de retrouver ![]() et
et ![]() ? Bonne chance. Si
? Bonne chance. Si ![]() est un nombre suffisamment grand, cette opération, appelée « factorisation », devient incroyablement difficile à réaliser. Les meilleurs ordinateurs du monde mettent des années à résoudre ce problème pour des nombres cryptographiques.
est un nombre suffisamment grand, cette opération, appelée « factorisation », devient incroyablement difficile à réaliser. Les meilleurs ordinateurs du monde mettent des années à résoudre ce problème pour des nombres cryptographiques.
C’est pourquoi la multiplication est une candidate intéressante pour une fonction à sens unique. Mais en pratique, il existe des constructions encore plus robustes et élégantes : l’arithmétique modulaire.
L’arithmétique modulaire : cache-cache avec des nombres
L’astuce en cryptographie, c’est de rendre encore plus compliqué de « remonter » au secret. Pour cela, on utilise l’arithmétique modulaire, une technique qui consiste à travailler avec des restes de division. En gros, au lieu de manipuler tous les nombres entiers, on « ramène » les résultats à une plage limitée. Voici un exemple :
![]()
Cela signifie que l’on divise ![]() par
par ![]() , et on garde seulement le reste. Par exemple :
, et on garde seulement le reste. Par exemple :
![]()
Ici, 37 divisé par 13 donne un reste de 11. Pourquoi est-ce utile ? Parce que cela ajoute une couche supplémentaire de complexité : si je vous donne ![]() et
et ![]() , retrouver
, retrouver ![]() devient impossible sans plus d’information.
devient impossible sans plus d’information.
Chapitre 3 : Exponentiation modulaire : multiplier des secrets comme un pro

L’addition, la soustraction, et même la multiplication, c’est bien joli, mais en cryptographie, ce n’est pas suffisant. Si vous voulez vraiment cacher vos secrets comme un agent double des maths, il faut passer à la vitesse supérieure : l’exponentiation modulaire. Rien que le nom fait frissonner, non ? C’est en fait une opération élégante et incroyablement utile, surtout pour créer des fonctions à sens unique.
Exponentiation : qu’est-ce que c’est ?
En maths, élever un nombre ![]() à une puissance
à une puissance ![]() signifie multiplier
signifie multiplier ![]() par lui-même
par lui-même ![]() fois. Par exemple :
fois. Par exemple :
![]()
Facile, non ? Mais dans notre contexte cryptographique, on rajoute un petit twist avec l’arithmétique modulaire. Ainsi, au lieu de calculer directement ![]() , on réduit le résultat modulo un nombre premier
, on réduit le résultat modulo un nombre premier ![]() :
:
![]()
Un exemple concret
Prenons ![]() ,
, ![]() , et
, et ![]() .
.
On commence par calculer ![]() :
:
![]()
Ensuite, on réduit ![]() modulo
modulo ![]() :
:
![]()
Ainsi, on obtient :
![]()
Vous voyez ? On a transformé ![]() en
en ![]() de manière apparemment simple… mais attendez de voir pourquoi ça devient si puissant.
de manière apparemment simple… mais attendez de voir pourquoi ça devient si puissant.
Pourquoi l’exponentiation modulaire est magique
Cette opération présente deux qualités cruciales pour la cryptographie :
- Facile à calculer : Même si
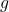 et
et 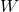 sont des nombres très grands, on peut calculer
sont des nombres très grands, on peut calculer 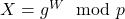 rapidement grâce à des astuces comme l’exponentiation rapide.
rapidement grâce à des astuces comme l’exponentiation rapide. - Difficile à inverser : Si je vous donne
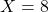 ,
, 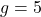 , et
, et 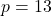 , il est incroyablement compliqué de retrouver
, il est incroyablement compliqué de retrouver 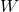 . Ce problème est connu sous le nom de logarithme discret. On y reviendra en détail dans un prochain chapitre.
. Ce problème est connu sous le nom de logarithme discret. On y reviendra en détail dans un prochain chapitre.
Un petit défi pour les amateurs
Essayez par vous-même :
- Calculez
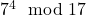 .
. - Retrouvez
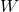 si
si 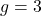 ,
, 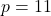 , et
, et 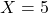 .
.
Bon courage pour le deuxième. Si vous y parvenez, vous êtes soit très talentueux… soit équipé d’un superordinateur (coucou la NSA).
Chapitre 4 : Logarithmes discrets : la quête du chiffre perdu

Vous souvenez-vous de la belle opération exponentiation modulaire du chapitre précédent ? C’était facile, non ? On prenait un nombre ![]() , on l’élevait à la puissance
, on l’élevait à la puissance ![]() , et on réduisait modulo
, et on réduisait modulo ![]() . Tout le monde y arrivait en un éclair.
. Tout le monde y arrivait en un éclair.
Mais voilà, en cryptographie, ce qui est facile à faire doit être difficile à défaire. Et quand il s’agit d’inverser cette opération, les choses se corsent. Bienvenue dans le monde fascinant du logarithme discret, l’un des piliers de la sécurité numérique moderne.
Qu’est-ce qu’un logarithme discret ?
En termes simples, si on vous donne une équation comme :
![]()
Votre mission est de retrouver ![]() . On appelle
. On appelle ![]() le logarithme discret de
le logarithme discret de ![]() en base
en base ![]() modulo
modulo ![]() . Notation :
. Notation :
![]()
Pourquoi c’est compliqué ?
Contrairement au logarithme classique qu’on apprend au lycée (genre ![]() ), le logarithme discret est une vraie bête noire. Pour des nombres suffisamment grands, il n’existe pas de méthode simple ou rapide pour résoudre ce problème. Voici pourquoi :
), le logarithme discret est une vraie bête noire. Pour des nombres suffisamment grands, il n’existe pas de méthode simple ou rapide pour résoudre ce problème. Voici pourquoi :
- L’exponentiation modulaire éparpille les valeurs de manière pseudo-aléatoire dans l’intervalle
![Rendered by QuickLaTeX.com [0, p-1]](https://pourton.info/wp-content/ql-cache/quicklatex.com-f0b2b66982ce37d799be20df248a9ebc_l3.png) . Même si vous voyez
. Même si vous voyez 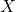 , il est impossible de « deviner » d’où il vient sans essayer toutes les possibilités.
, il est impossible de « deviner » d’où il vient sans essayer toutes les possibilités. - Les solutions possibles pour
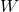 sont nombreuses : si
sont nombreuses : si 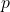 est grand (par exemple un nombre cryptographique de 2048 bits), il y a plus de
est grand (par exemple un nombre cryptographique de 2048 bits), il y a plus de 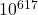 valeurs potentielles à tester. Bon courage.
valeurs potentielles à tester. Bon courage.
Exemple pour se faire mal
Prenons ![]() ,
, ![]() , et supposons que
, et supposons que ![]() . Trouver
. Trouver ![]() revient à résoudre :
revient à résoudre :
![]()
En essayant les valeurs de ![]() une par une (méthode brutale), on trouve finalement :
une par une (méthode brutale), on trouve finalement :
![]()
Car :![]()
Mais pour des nombres comme ![]() et
et ![]() , bonne chance pour résoudre ça à la main.
, bonne chance pour résoudre ça à la main.
Pourquoi c’est utile en cryptographie ?
Le logarithme discret est la raison pour laquelle des systèmes comme Diffie-Hellman ou ElGamal sont si robustes. Ces systèmes reposent sur l’hypothèse suivante :
L’exponentiation modulaire est facile, mais l’inversion via le logarithme discret est (pratiquement) impossible.
Et tant que cette hypothèse tient, vos secrets sont en sécurité.
Attaques et astuces
Bon, ce n’est pas parce que le problème est difficile qu’il est impossible. Des génies (ou des hackers, ça dépend du point de vue) ont développé des algorithmes pour résoudre certains cas particuliers. Par exemple :
- Pohlig-Hellman : fonctionne bien si
 est divisible par de petits facteurs premiers (on en reparlera).
est divisible par de petits facteurs premiers (on en reparlera). - Baby-step Giant-step : un algorithme qui accélère la recherche brute.
Mais même avec ces outils, la difficulté du problème reste exponentielle, ce qui le rend impraticable pour des nombres suffisamment grands.
Chapitre 5 : Quand Sophie Germain sauve vos mots de passe

Si vous pensez que vos mots de passe sont protégés uniquement grâce à de gros nombres aléatoires, détrompez-vous. Derrière la magie de la cryptographie, il y a des nombres bien particuliers, et parmi eux, les nombres premiers sûrs. Et qui mieux que Sophie Germain, l’une des plus grandes mathématiciennes de l’histoire, pour nous guider dans cet univers ?
Mais qu’est-ce qu’un nombre premier sûr ?
Un nombre premier sûr est un nombre premier ![]() qui vérifie cette propriété élégante :
qui vérifie cette propriété élégante :
![]()
où ![]() est aussi un nombre premier. Dit autrement,
est aussi un nombre premier. Dit autrement, ![]() est deux fois un autre nombre premier. Pourquoi est-ce utile ? Parce que cela renforce énormément la sécurité contre certaines attaques sur les logarithmes discrets.
est deux fois un autre nombre premier. Pourquoi est-ce utile ? Parce que cela renforce énormément la sécurité contre certaines attaques sur les logarithmes discrets.
Quelques exemples :
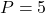 , car
, car 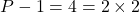 , et
, et 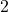 est premier.
est premier.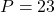 , car
, car 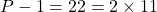 , et
, et  est premier.
est premier.
Ces nombres sont parfaits pour la cryptographie, car ils maximisent la « résistance mathématique » contre des algorithmes comme Pohlig-Hellman, qui dépendent de la factorisation de ![]() .
.
Pourquoi Sophie Germain ?
Sophie Germain, brillante mathématicienne du 19ᵉ siècle, a étudié ces nombres bien avant qu’ils ne deviennent la star de nos systèmes de chiffrement. Elle s’intéressait à des paires de nombres premiers ![]() , où
, où ![]() est un nombre premier de Germain (c’est ainsi qu’on les appelle en son honneur), et
est un nombre premier de Germain (c’est ainsi qu’on les appelle en son honneur), et ![]() .
.
Les premières paires de nombres premiers de Germain sont :
Elle les étudiait dans un tout autre contexte : le fameux grand théorème de Fermat, mais son travail a posé des bases théoriques solides pour des applications modernes. Aujourd’hui, on les utilise pour sécuriser vos connexions Wi-Fi. Si, si.
Pourquoi ça renforce la sécurité ?
Reprenons l’algorithme de Pohlig-Hellman. Il fonctionne bien lorsque ![]() est un « nombre friable », c’est-à-dire qu’il peut être décomposé en de nombreux petits facteurs premiers. Mais si
est un « nombre friable », c’est-à-dire qu’il peut être décomposé en de nombreux petits facteurs premiers. Mais si ![]() et que
et que ![]() est aussi un grand nombre premier, les attaques deviennent beaucoup plus compliquées, car il n’y a que deux facteurs à analyser :
est aussi un grand nombre premier, les attaques deviennent beaucoup plus compliquées, car il n’y a que deux facteurs à analyser : ![]() et
et ![]() .
.
En clair, les nombres premiers sûrs sont des forteresses mathématiques. Utiliser un nombre premier quelconque, comme ![]() , c’est comme laisser la porte ouverte à un hacker. (Oui, 13, tu as encore échoué.)
, c’est comme laisser la porte ouverte à un hacker. (Oui, 13, tu as encore échoué.)
Et aujourd’hui ?
Grâce aux progrès en algorithmique, on sait générer rapidement de très grands nombres premiers sûrs. Typiquement, les systèmes cryptographiques modernes utilisent des ![]() de 2048 bits (environ
de 2048 bits (environ ![]() ). Si
). Si ![]() est un nombre premier sûr, alors vos secrets sont protégés, même contre des supercalculateurs.
est un nombre premier sûr, alors vos secrets sont protégés, même contre des supercalculateurs.
Chapitre 6 : Diffie-Hellman : quand deux inconnus créent un secret partagé

Imaginez cette situation : Alice et Bob, deux parfaits inconnus, veulent partager un secret. Ils n’ont aucun moyen de se parler en privé, mais ils souhaitent tout de même établir une connexion sécurisée pour échanger des messages. Cela semble impossible, non ? C’est là que l’algorithme de Diffie-Hellman entre en jeu, un véritable tour de magie mathématique basé sur l’exponentiation modulaire et les logarithmes discrets.
Le principe de Diffie-Hellman
L’idée est simple : utiliser une fonction à sens unique pour que même si quelqu’un espionne la conversation, il soit incapable de découvrir le secret partagé. Voici comment ça fonctionne :
- Alice et Bob choisissent publiquement :
- Un nombre premier sûr
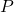 .
. - Une racine primitive
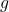 modulo
modulo 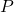 , un nombre spécial qui fait que les puissances successives de
, un nombre spécial qui fait que les puissances successives de 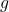 couvrent toutes les valeurs possibles modulo
couvrent toutes les valeurs possibles modulo 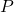 .
.
- Un nombre premier sûr
- Alice et Bob choisissent chacun un secret privé :
- Alice choisit un nombre
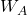 .
. - Bob choisit un nombre
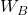 .
.
- Alice choisit un nombre
- Chacun calcule une clé publique :
- Alice calcule
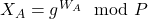 .
. - Bob calcule
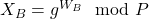 .
.
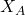 et
et 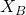 sont ensuite échangées publiquement. Là encore, Ève les voit.
sont ensuite échangées publiquement. Là encore, Ève les voit. - Alice calcule
- Ils calculent une clé partagée grâce à la propriété magique de l’exponentiation modulaire :
- Alice utilise
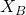 pour calculer
pour calculer 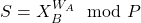 .
. - Bob utilise
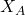 pour calculer
pour calculer 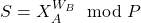 .
.
- Alice utilise
![]()
Alice et Bob obtiennent exactement le même résultat, sans jamais avoir à partager leur secret privé. Pendant ce temps, Ève, qui n’a accès qu’à ![]() ,
, ![]() ,
, ![]() , et
, et ![]() , est incapable de retrouver
, est incapable de retrouver ![]() sans résoudre un problème de logarithme discret. Bonne chance, Ève.
sans résoudre un problème de logarithme discret. Bonne chance, Ève.
Un exemple chiffré
Prenons des nombres simples :
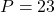 ,
, 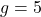 .
.- Alice choisit
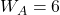 , donc
, donc 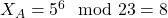 .
. - Bob choisit
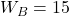 , donc
, donc 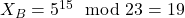 .
.
Alice et Bob échangent leurs clés publiques (![]() ,
, ![]() ).
).
- Alice calcule
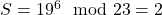 .
. - Bob calcule
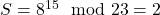 .
.
Le secret partagé est donc ![]() . Et Ève ? Même avec tout son talent, elle est bloquée.
. Et Ève ? Même avec tout son talent, elle est bloquée.
Pourquoi Diffie-Hellman est génial
- Simplicité et robustesse : L’algorithme repose uniquement sur des opérations mathématiques simples, mais sur des nombres si grands qu’ils deviennent impraticables à inverser.
- Sécurité : Tant que les logarithmes discrets restent difficiles à calculer, Diffie-Hellman est considéré comme inviolable.
- Applications universelles : De votre connexion Wi-Fi à votre navigation sur le web, cet algorithme est partout.
Et les calculateurs quantiques ?
Bien sûr, on sait déjà que les calculateurs quantiques mettront Diffie-Hellman en danger. Mais tant que ces machines ne sont pas fonctionnelles à grande échelle, l’algorithme reste une forteresse pour vos secrets.
Chapitre 7 : La signature cryptographique : prouvez que c’est vraiment vous (sans mot de passe)

Imaginez que vous envoyez une lettre à un ami, et qu’il puisse être sûr que vous êtes bien l’auteur, sans avoir besoin de vous voir signer en personne. En cryptographie, c’est exactement ce que permettent les signatures numériques : prouver que vous êtes l’expéditeur d’un message, sans doute possible, et sans échanger de mot de passe au préalable.
Une signature cryptographique repose sur deux ingrédients magiques : les clés asymétriques et les propriétés de l’exponentiation modulaire (oui, encore elle !).
Comment ça marche ?
Dans un système de signature numérique, chaque utilisateur possède :
- Une clé privée
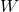 , secrète, qu’il garde pour lui.
, secrète, qu’il garde pour lui. - Une clé publique
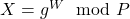 , qu’il partage avec le monde entier.
, qu’il partage avec le monde entier.
Ces deux clés sont liées mathématiquement, mais pas d’une manière qui permet de déduire ![]() à partir de
à partir de ![]() . Le lien entre elles est l’exponentiation modulaire, notre fonction à sens unique préférée.
. Le lien entre elles est l’exponentiation modulaire, notre fonction à sens unique préférée.
Signer un message
Quand vous voulez signer un message ![]() , vous effectuez un calcul qui prouve que vous connaissez
, vous effectuez un calcul qui prouve que vous connaissez ![]() , mais sans révéler
, mais sans révéler ![]() . Voici un exemple simplifié :
. Voici un exemple simplifié :
- Vous commencez par « hacher » le message
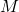 , en utilisant une fonction de hachage cryptographique
, en utilisant une fonction de hachage cryptographique 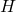 . Cette fonction transforme
. Cette fonction transforme 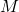 en un nombre
en un nombre 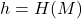 .
. - Ensuite, vous calculez votre signature
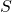 :
:
![]()
Cette signature ![]() est envoyée avec le message
est envoyée avec le message ![]() .
.
Vérifier la signature
Pour vérifier que ![]() vient bien de vous, le destinataire fait ce qui suit :
vient bien de vous, le destinataire fait ce qui suit :
- Il récupère votre clé publique
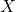 .
. - Il calcule :
![]()
Si cette valeur correspond à ![]() , alors il est sûr que vous êtes bien l’auteur du message. Pourquoi ? Parce que seul quelqu’un connaissant
, alors il est sûr que vous êtes bien l’auteur du message. Pourquoi ? Parce que seul quelqu’un connaissant ![]() aurait pu produire
aurait pu produire ![]() .
.
Un exemple pour les amateurs de chiffres
Supposons que :
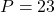 ,
, 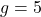 ,
, 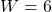 (votre clé privée).
(votre clé privée).- Votre clé publique est donc
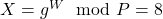 .
.
Vous voulez signer un message avec ![]() (le hash du message).
(le hash du message).
- Vous calculez :
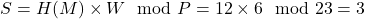 .
. - Vous envoyez
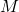 et
et 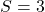 .
.
Le destinataire, qui connaît ![]() , vérifie :
, vérifie :![]() .
.
Les valeurs correspondent ! Il sait donc que le message est bien de vous.
Pourquoi c’est utile ?
La signature numérique est essentielle dans des domaines comme :
- Les transactions bancaires : Prouver que vous êtes bien l’auteur d’une opération.
- Les certificats SSL/TLS : Garantir que vous communiquez avec le bon site web.
- Les documents légaux : Authentifier une signature électronique.
Mais attention…
Comme toujours, la sécurité repose sur la difficulté du logarithme discret. Si jamais un hacker arrive à retrouver ![]() à partir de
à partir de ![]() , il pourra se faire passer pour vous. Et c’est là que les calculateurs quantiques risquent de changer la donne… Mais nous y reviendrons plus tard.
, il pourra se faire passer pour vous. Et c’est là que les calculateurs quantiques risquent de changer la donne… Mais nous y reviendrons plus tard.
Chapitre 8 : La menace quantique : faut-il dire adieu à nos secrets ?

Tout au long de cet article, nous avons exploré des concepts fascinants : fonctions à sens unique, logarithmes discrets, exponentiation modulaire, nombres premiers sûrs, et bien sûr, les algorithmes comme Diffie-Hellman ou les signatures numériques. Mais tout cela repose sur une hypothèse fondamentale : que résoudre ces problèmes est trop difficile, même pour les ordinateurs les plus puissants d’aujourd’hui.
Et c’est là qu’arrive le méchant du film : le calculateur quantique.
Qu’est-ce qu’un calculateur quantique ?
Un calculateur quantique, c’est une machine qui utilise les lois bizarres de la mécanique quantique pour résoudre certains problèmes bien plus rapidement que n’importe quel ordinateur classique. Dans le contexte de la cryptographie, deux problèmes sont particulièrement en danger :
- La factorisation : le fondement de systèmes comme RSA.
- Le logarithme discret : la base de Diffie-Hellman, ElGamal, et d’autres.
Grâce à l’algorithme de Shor, un calculateur quantique pourrait inverser ces fonctions à sens unique en un temps polynomial. Traduction : ce qui était considéré comme pratiquement impossible pourrait devenir faisable.
Une menace réelle ?
Heureusement, les calculateurs quantiques ne sont pas encore capables de casser vos secrets :
- Ils sont encore limités en taille et en fiabilité.
- Ils demandent des ressources immenses pour fonctionner.
Mais les experts estiment qu’il faudra 20 à 30 ans avant que ces machines deviennent une menace réelle. C’est à la fois rassurant… et inquiétant. Pourquoi ? Parce que les données sensibles chiffrées aujourd’hui pourraient être décryptées demain. On appelle cela le modèle « Harvest now, decrypt later » (collecter maintenant, déchiffrer plus tard).
La cryptographie post-quantique
Face à cette menace, les mathématiciens et cryptographes travaillent déjà sur des solutions dites post-quantiques. Ces nouvelles approches reposent sur des problèmes mathématiques différents, comme :
- Les réseaux euclidiens : des grilles multidimensionnelles très complexes.
- Les codes correcteurs d’erreurs : utilisés pour cacher l’information dans des ensembles énormes.
- Les isogénies de courbes elliptiques : un concept encore plus sophistiqué que les courbes elliptiques classiques.
Ces systèmes sont conçus pour résister, même aux calculateurs quantiques.
Faut-il s’inquiéter ?
Pas encore, mais il est urgent de s’y préparer. La cryptographie moderne a évolué en réponse aux progrès technologiques, et elle continuera de le faire. Tant qu’il y aura des secrets à protéger, il y aura des mathématiciens pour inventer de nouvelles façons de les sécuriser.
Un dernier mot
Les maths ne servent pas qu’à résoudre des équations dans un manuel. Elles protègent vos communications, vos finances, et même votre vie privée. Alors, la prochaine fois que vous vous connectez à un site web ou envoyez un message chiffré, pensez à tout le génie mathématique derrière ces simples opérations.
Chapitre 9 : Cryptographie post-quantique : l’avenir des secrets numériques

Quand on parle de calculateur quantique, c’est comme si on évoquait un tsunami informatique qui pourrait déferler sur la cryptographie actuelle. Les systèmes que nous utilisons aujourd’hui pour protéger nos secrets risquent de devenir obsolètes face à cette nouvelle technologie. Mais rassurez-vous, les mathématiciens ont déjà commencé à bâtir des digues : bienvenue dans l’univers fascinant de la cryptographie post-quantique.
Qu’est-ce que la cryptographie post-quantique ?
C’est un ensemble de techniques et d’algorithmes conçus pour résister aux attaques d’un calculateur quantique. Contrairement à RSA ou Diffie-Hellman, qui reposent sur la difficulté des logarithmes discrets ou de la factorisation, ces nouvelles approches s’appuient sur des problèmes mathématiques totalement différents.
Voici quelques candidats prometteurs :
- Les réseaux euclidiens
Imaginez une grille en plusieurs dimensions, comme une sorte de quadrillage 3D (ou 1000D, soyons ambitieux). Le problème consiste à trouver le point le plus proche d’un autre dans cette grille.
Ce problème, appelé le Shortest Vector Problem (SVP), est tellement complexe que même un calculateur quantique s’y casserait les dents. - Les codes correcteurs d’erreurs
Ces algorithmes cachent les données dans un immense espace mathématique, puis utilisent des techniques de correction pour les récupérer. Cela rend les attaques par force brute pratiquement impossibles, car il faudrait explorer des milliards de milliards de possibilités. - Les isogénies de courbes elliptiques
Si les courbes elliptiques classiques ont déjà révolutionné la cryptographie, leurs cousines, les isogénies, pourraient bien être l’avenir. Ces courbes permettent de créer des systèmes encore plus résistants grâce à leurs structures mathématiques hyper-complexes. - Les fonctions de hachage
Certaines techniques reposent uniquement sur la difficulté de retrouver l’entrée d’une fonction de hachage à partir de sa sortie. Simples mais efficaces, elles offrent une base solide pour construire des signatures et des clés.
Un exemple post-quantique : le chiffrement basé sur les réseaux
Prenons un cas pratique. Imaginez une grille en 2D, avec des points régulièrement espacés. Si je vous donne un point ![]() , légèrement décalé, et vous demande de trouver le point de la grille le plus proche, cela semble simple, non ?
, légèrement décalé, et vous demande de trouver le point de la grille le plus proche, cela semble simple, non ?
Maintenant, imaginez cette grille en 1024 dimensions, avec des millions de points potentiels. Soudain, ce problème devient incroyablement difficile, même pour un calculateur quantique. C’est exactement ce que fait le chiffrement basé sur les réseaux : il cache vos données dans ce labyrinthe multidimensionnel.
La course contre le temps
Alors que des calculateurs quantiques fonctionnels sont encore loin, la cryptographie post-quantique est déjà en train d’être standardisée. L’organisme américain NIST (National Institute of Standards and Technology) a lancé un processus pour sélectionner les algorithmes qui protégeront nos données à l’avenir. Parmi les finalistes, on retrouve des noms comme Kyber, Dilithium, ou encore FrodoKEM.
Ces algorithmes ne remplacent pas simplement RSA ou Diffie-Hellman : ils redéfinissent totalement la manière dont nous pensons la sécurité.
Devons-nous tout changer dès maintenant ?
Pas nécessairement. Les systèmes actuels, basés sur les logarithmes discrets et la factorisation, restent solides face aux ordinateurs classiques. Mais les entreprises, les gouvernements, et même les particuliers devraient commencer à se préparer en adoptant des solutions hybrides :
- Combiner les systèmes actuels avec des approches post-quantiques.
- Identifier les données sensibles qui devront rester protégées sur le long terme.
Une nouvelle ère pour les mathématiques
La cryptographie post-quantique ouvre aussi de nouveaux horizons pour les mathématiciens. Elle les pousse à explorer des domaines encore peu étudiés, comme les structures algébriques complexes ou la théorie des graphes. Comme toujours, c’est un rappel que les mathématiques sont à la fois un bouclier et une épée dans notre monde numérique.
Chapitre 10 : Ce que les maths nous apprennent sur la sécurité (et sur nous-mêmes)

Après ce long voyage dans le monde fascinant de la cryptographie, une chose est claire : derrière chaque connexion sécurisée, chaque message confidentiel, et chaque transaction bancaire, il y a une armée invisible de concepts mathématiques. Mais au-delà de ces outils, les maths nous enseignent bien plus que la sécurité numérique.
Les mathématiques, une arme et un bouclier
Depuis l’invention des premiers chiffrements jusqu’à l’émergence des calculateurs quantiques, les mathématiques ont toujours été à la fois l’arme des attaquants et le bouclier des défenseurs. Chaque avancée dans la cryptanalyse pousse les cryptographes à innover, et chaque innovation inspire de nouveaux défis. C’est un jeu d’échecs millénaire, où chaque coup révèle la beauté et la complexité des nombres.
Une discipline au service de tous
La cryptographie n’est pas réservée aux espions ou aux banques. Aujourd’hui, elle protège :
- Votre vie privée : Les applications de messagerie chiffrée comme WhatsApp ou Signal s’appuient sur Diffie-Hellman et d’autres algorithmes pour garantir que vos discussions restent confidentielles.
- Votre argent : Les systèmes de paiement en ligne, les crypto-monnaies comme Bitcoin, et même les guichets automatiques dépendent de la robustesse des algorithmes cryptographiques.
- Votre identité : Les signatures numériques permettent de prouver que vous êtes bien vous, sans avoir à partager un mot de passe ou une clé physique.
Et tout cela, c’est grâce à une discipline que beaucoup considèrent (à tort !) comme abstraite ou inutile : les mathématiques.
Une leçon d’humilité
Si les fonctions à sens unique et les logarithmes discrets nous protègent aujourd’hui, c’est parce que nous n’avons pas encore trouvé de méthode efficace pour les inverser. Mais les calculateurs quantiques nous rappellent que rien n’est éternel. Ce que nous considérons comme « incassable » aujourd’hui pourrait être trivial demain. Les maths nous enseignent l’humilité : elles nous rappellent que notre sécurité dépend de notre capacité à innover constamment.
L’avenir appartient aux curieux
Les mathématiques ne sont pas figées. Elles évoluent avec nous, au rythme des défis de chaque époque. Qu’il s’agisse de trouver de nouveaux nombres premiers, d’explorer des courbes elliptiques exotiques, ou de concevoir des systèmes post-quantiques, une chose est certaine : les maths continueront d’être au cœur de notre monde numérique.
Et vous ? Que ferez-vous avec ce que vous avez appris ? Peut-être contribuerez-vous à résoudre l’un des grands mystères mathématiques, ou à développer les systèmes qui protégeront les générations futures. Ou peut-être, simplement, regarderez-vous votre connexion Wi-Fi avec un nouveau respect.
La sécurité, c’est une question de maths (et de passion)
La cryptographie moderne repose sur un mélange fascinant de rigueur mathématique, d’intuition, et de créativité. Et derrière chaque équation, il y a des personnes qui travaillent sans relâche pour protéger vos secrets. Alors, que ce soit pour envoyer un emoji ou pour sécuriser un vote en ligne, souvenez-vous : tout cela est possible grâce aux maths.
Et qui sait ? Peut-être qu’un jour, ce sera vous qui écrirez les équations du futur.
 Pourton.info
Pourton.info 



