La Relativité du Quotidien : Pourquoi Votre Maison Rétrécit Quand Vous Roulez Trop Vite (ou Presque)

8 novembre 2024 Actualité

La Relativité de l’Absurdement Simple

En 1900, alors que le monde entre dans un nouveau siècle avec espoir et progrès, Lord Kelvin, célèbre physicien britannique, monte sur scène pour déclarer que la physique est « presque » complète. Il affirme que toutes les lois de la nature ont été découvertes, et que la science n’a plus qu’à résoudre quelques derniers détails techniques. Mais attention, deux petits « nuages » viennent troubler cette belle image.

Ces deux anomalies, à première vue insignifiantes, cachent en réalité des révolutions en sommeil, prêtes à redéfinir toute la physique moderne. Commençons par les identifier.

Nuage n°1 : Le mystère du rayonnement du Soleil

Le premier nuage concerne notre étoile préférée, le Soleil. À l’époque, les lois de la thermodynamique et de la physique classique peinent à expliquer pourquoi le Soleil émet autant d’énergie. Selon les équations en vigueur, un corps chauffé émet des radiations, mais il devrait rapidement perdre toute son énergie – or, notre Soleil brille sans faiblir ! Ce mystère semblera absurde des décennies plus tard quand la mécanique quantique apparaîtra, mais à l’époque, ce manque d’explication fait grincer les dents des scientifiques.

Nuage n°2 : L’expérience de Michelson et Morley – Quand la lumière fait la sourde oreille

Le second nuage est encore plus intriguant. En 1887, Albert A. Michelson et Edward W. Morley, deux physiciens américains, conçoivent une expérience censée mesurer la vitesse de la lumière en tenant compte du mouvement de la Terre. Leur hypothèse repose sur l’idée que l’univers est rempli d’un « éther », une sorte de fluide invisible dans lequel la lumière se déplace, tout comme le son se propage dans l’air. Si la Terre se déplace à travers cet éther, la lumière devrait aller plus vite dans une direction que dans l’autre, un peu comme un bateau qui lutte ou profite d’un courant.

Leur dispositif, un interféromètre ultra-sensible, est installé avec une précision incroyable pour détecter la moindre variation de la vitesse de la lumière. Mais le résultat… c’est le néant. Aucune différence n’est mesurée, et la lumière semble ignorer royalement le mouvement de la Terre. Que la Terre bouge ou reste immobile, la lumière se déplace toujours à la même vitesse, soit environ 299,792 , \text{km/s}. Pour les physiciens, c’est une énigme monumentale.

Le Principe de Relativité : Quand Tout le Monde a Raison (Même en Physique !)

Pour comprendre pourquoi cette expérience est si troublante, il faut introduire un principe fondamental : le principe de relativité. Déjà formulé par Galilée, il affirme que les lois de la physique s’appliquent de la même manière pour tous les observateurs, qu’ils soient en mouvement constant ou à l’arrêt. Si vous êtes dans un train en mouvement à vitesse constante, vous pouvez jouer à la balle sans remarquer que vous bougez. La balle se comporte comme si vous étiez sur un quai. Galilée nous dit : tout mouvement est relatif.

Jusqu’ici, rien de dramatique. Mais là où la relativité classique et l’expérience de Michelson-Morley se heurtent, c’est sur la question de la vitesse de la lumière. En effet, si on suit la logique de Galilée, on devrait pouvoir additionner des vitesses. Par exemple, si vous êtes dans un train à 100 , \text{km/h} et que vous lancez une balle à 30 , \text{km/h} vers l’avant, la balle se déplace à 130 , \text{km/h} par rapport au sol.

Mais l’expérience de Michelson et Morley indique que la lumière, elle, refuse de jouer ce jeu ! Sa vitesse reste 299,792 , \text{km/s}, peu importe la direction ou la vitesse de l’observateur. Cela défie non seulement le bon sens, mais aussi les bases mêmes de la physique de l’époque.

L’Incroyable Hypothèse à Venir

Le problème devient si épineux que certains scientifiques – Lorentz, Larmor, et plus tard Einstein – envisagent une hypothèse radicale. Et si les objets se contractaient légèrement dans le sens du mouvement lorsqu’ils approchent de la vitesse de la lumière ? Et si, au lieu de se contenter de lois « absolues », la physique dépendait du point de vue de chaque observateur, bouleversant ainsi notre perception de l’espace et du temps ? Spoiler : cela va devenir le socle de la relativité restreinte !

C’est donc à partir de cette situation absurde, où la lumière fait fi des vitesses relatives, que l’on va partir dans notre voyage à travers les idées de la relativité. Prêts pour la suite ? Alors continuons !

Les Folles Hypothèses de Lorentz : La Contraction des Longueurs en Question

Alors que l’expérience de Michelson et Morley laisse les physiciens perplexes, certains d’entre eux se lancent dans des hypothèses audacieuses pour expliquer ce comportement étrange de la lumière. Le premier à proposer une solution digne de la science-fiction est Hendrik Lorentz, un physicien néerlandais. Son idée est simple… et radicale : si un objet se déplace très vite, sa longueur se contracte dans la direction de son mouvement.

Lorentz et la « Contraction des Longueurs »

Lorentz part du principe que pour concilier les résultats de l’expérience de Michelson-Morley avec les lois de la physique, il faut accepter que les objets ne restent pas rigides quand ils se déplacent à grande vitesse. Pour lui, si un objet se rapproche de la vitesse de la lumière, il se contracte un peu, comme une sorte de compression cosmique invisible.

Imaginons un train lancé à une vitesse folle. Selon Lorentz, si ce train s’approchait de la vitesse de la lumière, il apparaîtrait plus court pour un observateur extérieur, comme si l’univers entier jouait au Photoshop en temps réel ! Ce phénomène est ce qu’on appelle la contraction des longueurs.

La Formule de Contraction de Lorentz : Bienvenue à Gamma !

Pour quantifier cette contraction, Lorentz introduit un facteur, appelé aujourd’hui le facteur de Lorentz, souvent noté par la lettre grecque \gamma (« gamma »). La formule de contraction des longueurs est alors la suivante :

L = L_0 \frac{1}{\gamma}

où :

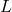  • L est la longueur mesurée pour un observateur extérieur, c’est-à-dire celui qui voit l’objet bouger ;
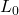  • L_0 est la longueur propre, c’est-à-dire la longueur mesurée par quelqu’un qui se déplace avec l’objet (imaginez un passager dans le train) ;
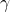  • \gamma est le facteur de Lorentz défini par :

\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}

où :

  • v est la vitesse de l’objet ;
  • c est la vitesse de la lumière dans le vide, soit environ 299,792 , \text{km/s}.

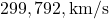Comprendre Gamma : La Taille Diminue avec la Vitesse

Cette formule nous dit quelque chose d’étonnant : plus la vitesse de l’objet approche celle de la lumière, plus \gamma devient grand, et donc plus L se réduit. Pour illustrer cela, regardons quelques exemples chiffrés :

  • Si 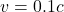v = 0.1c (10 % de la vitesse de la lumière), alors 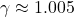\gamma \approx 1.005. La contraction est minuscule, presque imperceptible.
  • Si 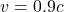v = 0.9c (90 % de la vitesse de la lumière), alors 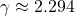\gamma \approx 2.294, et la longueur apparente de l’objet est environ divisée par 2.3 !
  • À 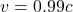v = 0.99c (99 % de la vitesse de la lumière), 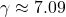\gamma \approx 7.09 : l’objet ne mesure plus qu’un septième de sa taille d’origine !

Cela signifie que, pour un observateur extérieur, un objet se rapprochant de la vitesse de la lumière devient réellement plus petit dans le sens de son mouvement.

Pourquoi cette Contraction ? De l’Éther à l’Illusion

Pour Lorentz, cette contraction des longueurs est une sorte de « correction cosmique » permettant de maintenir la vitesse de la lumière constante, même si la Terre bouge. L’idée est que l’univers « contracte » les objets en fonction de leur vitesse, afin de maintenir les apparences.

Mais cette explication amène une question fondamentale : est-ce que cette contraction est « réelle » ? Est-ce que l’objet lui-même « ressent » cette compression, ou est-ce une illusion d’optique cosmique ? Pour Lorentz, la contraction est bien réelle ; il pense que les objets se déforment véritablement.

Einstein, lui, va reprendre cette idée, mais avec une touche de génie qui changera tout : pour lui, ce n’est pas l’univers qui joue des tours en contractant les longueurs. Au lieu de cela, il redéfinit notre perception même de l’espace et du temps. C’est ce qui nous amène au concept de la relativité restreinte.

Einstein Entre en Scène : La Simultanéité, C’est Relatif

En 1905, un jeune employé de bureau nommé Albert Einstein publie un article qui va bouleverser notre compréhension de l’univers. Là où Lorentz et les autres voient dans la contraction des longueurs une simple « correction cosmique », Einstein va un cran plus loin : pour lui, c’est notre vision de l’espace et du temps qui est à revoir.

Deux Principes Simples mais Explosifs

Pour construire sa théorie, Einstein s’appuie sur deux principes qui, mis ensemble, semblent défier la logique. On les appelle aujourd’hui les postulats de la relativité restreinte :

  1. Le principe de relativité : les lois de la physique sont les mêmes dans tous les référentiels inertiels (c’est-à-dire pour des observateurs qui ne subissent pas d’accélération). Que vous soyez dans un train ou sur un quai, les lois de la physique fonctionnent de la même manière.
  2. La constance de la vitesse de la lumière : la vitesse de la lumière dans le vide est la même pour tous les observateurs, peu importe leur vitesse ou la direction de leur mouvement. Autrement dit, qu’un vaisseau spatial fonce vers une source de lumière ou s’en éloigne, il mesurera toujours la même vitesse de la lumière, soit 299,792 , \text{km/s}.

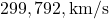Ces deux postulats, combinés, semblent mener à une absurdité : si la vitesse de la lumière est la même pour tous les observateurs, alors certaines de nos intuitions fondamentales sur l’espace et le temps doivent être fausses.

La Simultanéité est Relative

L’une des premières conséquences de la théorie d’Einstein est que la simultanéité est relative. Cela signifie que deux événements qui semblent se produire en même temps pour un observateur ne le seront pas forcément pour un autre.

Prenons un exemple pour clarifier cette idée. Imaginez un train en mouvement à grande vitesse. Deux éclairs frappent simultanément les extrémités avant et arrière du train. Pour un observateur situé au milieu du train, les éclairs semblent frapper exactement en même temps. Mais pour un observateur qui regarde depuis le quai, cela n’est pas le cas : il verra d’abord l’éclair qui frappe l’avant, puis celui qui frappe l’arrière, car le train se déplace vers l’avant au moment de l’éclair.

Cela s’explique simplement par le fait que la lumière des deux éclairs doit parcourir différentes distances pour atteindre chaque observateur. Puisque la vitesse de la lumière est constante et que le train est en mouvement, cette différence de distance implique une différence dans le moment où chaque éclat de lumière atteint les observateurs.

Mathématisons la Simultanéité Relative

Pour quantifier cette différence, Einstein utilise des transformations mathématiques, les fameuses transformations de Lorentz, qui relient les coordonnées spatiales et temporelles d’un événement dans différents référentiels. Pour un événement en mouvement dans un référentiel, les transformations de Lorentz sont les suivantes :

  1. Transformation de l’espace :
    x' = \gamma \left( x - vt \right)
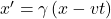
  2. Transformation du temps :
    t' = \gamma \left( t - \frac{vx}{c^2} \right)

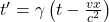
où :

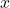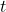  • x et t sont la position et le temps mesurés par un observateur dans un référentiel fixe (comme le quai),
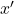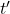  • x' et t' sont la position et le temps dans le référentiel en mouvement (comme le train),
  • v est la vitesse relative entre les deux référentiels,
  • c est la vitesse de la lumière,
  • \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}.

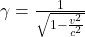Ces équations montrent que le temps et l’espace ne sont pas absolus ; ils dépendent du référentiel. En particulier, t' et t ne sont pas toujours égaux, même si l’événement est le même pour les deux observateurs.

Un Changement Radical : La Fin de l’Espace et du Temps Absolus

Avec ces transformations, Einstein nous dit quelque chose de profond : le temps et l’espace sont relatifs. Ce que nous appelons simultanéité dépend de l’observateur. En d’autres termes, l’espace et le temps ne sont pas des entités séparées et fixes, mais des aspects d’une seule et même réalité dynamique : l’espace-temps.

Einstein conclut que si l’on veut mesurer un événement dans l’espace et le temps, on doit prendre en compte le mouvement de l’observateur. Cette idée de simultanéité relative ouvre la porte à des concepts qui vont révolutionner la physique, notamment le fait que le temps et l’espace peuvent se contracter et se dilater en fonction de la vitesse et du point de vue de l’observateur.

La Contraction des Longueurs : Quand Tout Devient Plus Court en Mouvant

Avec l’idée que la simultanéité dépend de l’observateur, Einstein introduit une nouvelle vision de la contraction des longueurs. Pour lui, ce n’est pas une simple « correction cosmique » : c’est un effet physique bien réel, intrinsèque au tissu de l’espace-temps.

Comprendre la Contraction : Pourquoi les Objets Racourcissent-ils en Mouvement ?

La contraction des longueurs s’applique uniquement dans la direction du mouvement. Elle ne signifie pas que l’objet « se déforme » de manière perceptible par un observateur qui se déplace avec lui ; pour cet observateur, tout reste identique. C’est plutôt pour un observateur extérieur, immobile, que l’objet semble « raccourcir » à mesure qu’il s’approche de la vitesse de la lumière.

Voici la formule précise de la contraction des longueurs, que nous avons introduite dans le chapitre précédent, mais que nous allons détailler ici :

L = L_0 \sqrt{1 - \frac{v^2}{c^2}}

où :

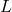  • L est la longueur apparente pour un observateur extérieur (par exemple, quelqu’un sur le quai),
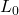  • L_0 est la longueur propre, mesurée par un observateur se déplaçant avec l’objet (un passager dans le train),
  • v est la vitesse de l’objet par rapport à l’observateur,
  • c est la vitesse de la lumière dans le vide.

Visualiser la Contraction avec Gamma

Revenons un instant au facteur \gamma introduit plus tôt :

\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}

Le terme \sqrt{1 - \frac{v^2}{c^2}} étant toujours inférieur à 1, L sera toujours plus petit que L_0 tant que v \neq 0. Cela signifie qu’à mesure que la vitesse augmente, la longueur apparente de l’objet diminue.

Pour rendre cela encore plus clair, prenons quelques exemples chiffrés :

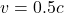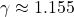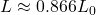  • Si v = 0.5c (50 % de la vitesse de la lumière), alors \gamma \approx 1.155, et L \approx 0.866L_0. L’objet semble environ 13 % plus court.
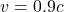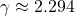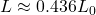  • Si v = 0.9c, alors \gamma \approx 2.294, et L \approx 0.436L_0. La longueur apparente est maintenant réduite à environ 44 % de sa taille d’origine !
  • À 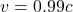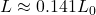v = 0.99c, L \approx 0.141L_0, soit environ 14 % de la longueur propre. On observe donc une contraction spectaculaire.

Pourquoi la Contraction des Longueurs n’Est-elle Pas « Ressentie » ?

Un détail essentiel de la contraction des longueurs est que l’objet ne se perçoit pas lui-même comme contracté. Si vous êtes dans le train ou à bord d’un vaisseau voyageant à des vitesses proches de celle de la lumière, vous mesureriez sa longueur et constateriez qu’elle est normale. C’est seulement pour les observateurs extérieurs, qui vous voient filer à toute vitesse, que l’objet semble raccourci.

Pour comprendre pourquoi, revenons à la simultanéité relative. Lorsque nous voulons mesurer la longueur d’un objet, nous devons mesurer ses extrémités « en même temps ». Mais avec la relativité, ce « en même temps » change d’un observateur à l’autre. Cela signifie que les deux observateurs ne sont pas d’accord sur ce qu’ils appellent « la longueur ».

Ainsi, pour un observateur fixe, la contraction des longueurs apparaît simplement parce que les événements de mesure des extrémités de l’objet ne sont pas simultanés comme ils le sont pour l’observateur en mouvement. En d’autres termes, la contraction des longueurs est une conséquence directe de la relativité de la simultanéité.

La Contraction des Longueurs dans la Vie Pratique ?

Alors, cette contraction est-elle observable ? Oui, mais seulement à des vitesses colossales. Par exemple, même un avion de chasse à 2,000 , \text{km/h} ne subit qu’une contraction infime, car sa vitesse est négligeable face à celle de la lumière. Cependant, les particules accélérées dans des accélérateurs comme le LHC (Large Hadron Collider) approchent des vitesses relativistes, et leur contraction devient mesurable. Les scientifiques tiennent compte de cette contraction dans leurs calculs et leurs observations.

Cette contraction des longueurs, conséquence de la relativité de la simultanéité, est un phénomène réel dans l’espace-temps relativiste, bien que ses effets ne soient perceptibles que dans des conditions extrêmes.

La Dilatation du Temps : Quand Une Minute Devient Une Éternité (ou Presque)

Nous avons vu que pour les observateurs en mouvement par rapport à un objet, ce dernier semble se contracter dans la direction de son mouvement. Mais ce n’est pas la seule bizarrerie introduite par la relativité restreinte d’Einstein. En plus de l’espace qui se contracte, le temps lui-même se dilate, comme si l’univers jouait avec un élastique.

Le Temps qui Ralentit : Comment et Pourquoi ?

Imaginons que vous soyez dans un vaisseau spatial filant à une vitesse proche de celle de la lumière. Selon la relativité restreinte, le temps dans ce vaisseau s’écoule plus lentement pour vous que pour quelqu’un resté sur Terre. Cela signifie que, pendant qu’une année passe pour vous dans le vaisseau, il peut s’écouler plusieurs années pour un observateur terrestre.

Ce phénomène, que l’on appelle dilatation du temps, peut être quantifié par le même facteur \gamma que celui que nous avons vu pour la contraction des longueurs. La formule de la dilatation du temps est la suivante :

\Delta t = \gamma , \Delta t_0

où :

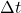  • \Delta t est l’intervalle de temps mesuré par un observateur extérieur (quelqu’un sur Terre),
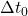  • \Delta t_0 est l’intervalle de temps propre, mesuré par un observateur qui se déplace avec l’objet (comme dans le vaisseau),
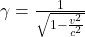  • \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} est, encore une fois, le facteur de Lorentz.

Cette formule signifie qu’à mesure que la vitesse de l’objet approche celle de la lumière, \gamma augmente, et donc l’intervalle de temps \Delta t mesuré par un observateur extérieur devient de plus en plus grand par rapport à l’intervalle de temps propre \Delta t_0.

Exemple : Un Voyage Relativiste

Supposons qu’un vaisseau spatial voyage à v = 0.8c (80 % de la vitesse de la lumière). Le facteur de Lorentz dans ce cas est :

\gamma = \frac{1}{\sqrt{1 - \frac{(0.8c)^2}{c^2}}} = \frac{1}{\sqrt{1 - 0.64}} \approx 1.667

Cela signifie que pour chaque seconde écoulée dans le vaisseau (\Delta t_0 = 1 seconde), l’observateur extérieur mesure un temps \Delta t = 1.667 secondes. Ainsi, le temps semble s’étirer pour l’observateur immobile, tandis que pour l’astronaute dans le vaisseau, tout semble parfaitement normal.

Comprendre la Dilatation du Temps avec une Horloge à Lumière

Pour illustrer cette dilatation, imaginons une « horloge à lumière », un appareil simple qui compte le temps en mesurant combien de fois un faisceau de lumière rebondit entre deux miroirs.

Si cette horloge est en mouvement rapide par rapport à un observateur extérieur, la lumière devra parcourir une plus grande distance entre les miroirs (car l’horloge elle-même bouge). Cependant, comme la vitesse de la lumière est constante, cela signifie que le temps entre chaque rebond doit augmenter. Autrement dit, le temps s’écoule plus lentement pour l’horloge en mouvement.

La Dilatation du Temps dans la Vie Quotidienne ?

Comme pour la contraction des longueurs, cette dilatation du temps n’est perceptible que pour des vitesses très élevées. Cependant, ce phénomène a été vérifié expérimentalement. Les particules subatomiques, comme les muons, sont créées dans l’atmosphère terrestre lors de l’impact de rayons cosmiques. En raison de leur vitesse proche de celle de la lumière, leur durée de vie, qui devrait être de quelques microsecondes, s’étire suffisamment pour qu’ils atteignent la surface de la Terre avant de se désintégrer. Cela est dû à la dilatation du temps !

Les horloges atomiques placées dans des avions de ligne subissent également une dilatation du temps, confirmant que le temps s’écoule plus lentement pour des objets en mouvement. Ce phénomène est si précis qu’il doit être pris en compte dans les systèmes GPS : les satellites en orbite, en mouvement rapide, voient leur temps se dilater légèrement par rapport aux horloges terrestres, et cette correction est cruciale pour la précision des localisations.

Espace-Temps : Quand l’Espace et le Temps ne Font Qu’Un

Au début du XXe siècle, la physique reposait sur une idée simple : l’espace et le temps sont deux entités distinctes. L’espace était l’endroit où les choses se produisaient, tandis que le temps permettait de dire quand elles se produisaient. Mais en unifiant la contraction des longueurs et la dilatation du temps, Einstein introduit un concept encore plus radical : l’espace-temps, une seule et même entité qui relie l’espace et le temps dans un même cadre.

L’Invariance de l’Intervalle d’Espace-Temps

Imaginez que vous soyez un explorateur cosmique, et que vous observiez deux événements qui se produisent à une certaine distance l’un de l’autre, avec un certain décalage temporel. Pour deux observateurs en mouvement relatif, ces événements auront des valeurs différentes de distance et de durée. Pourtant, la combinaison de l’espace et du temps pour ces événements reste toujours la même. C’est ce qu’on appelle l’intervalle d’espace-temps, une sorte de « distance » qui lie l’espace et le temps.

L’intervalle d’espace-temps, noté s, est donné par la formule suivante :

s^2 = c^2 \Delta t^2 - \Delta x^2

où :

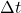  • \Delta t est l’intervalle de temps entre les deux événements,
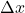  • \Delta x est la distance spatiale entre les deux événements,
  • c est la vitesse de la lumière.

Si s^2 est positif, les deux événements sont séparés par une « distance temporelle » (ils peuvent être reliés causalement). Si s^2 est négatif, les deux événements sont séparés par une « distance spatiale ». Si s^2 = 0, on dit qu’ils sont séparés par une « distance lumière », car seule la lumière pourrait relier ces deux événements en se déplaçant à la vitesse c.

Pourquoi l’Intervalle est-il Invariant ?

Cet intervalle d’espace-temps est invariant, ce qui signifie qu’il reste le même pour tous les observateurs, peu importe leur vitesse relative. C’est une révélation incroyable, car cela signifie que même si chaque observateur voit des longueurs et des temps différents, la structure sous-jacente de l’espace-temps est la même pour tous.

L’idée est que, dans l’espace-temps, chaque observateur a sa propre vision de l’espace et du temps, mais tous peuvent se mettre d’accord sur la « distance » entre les événements dans cet espace-temps. Cela confère une certaine objectivité à un monde où tout semble relatif.

Le Diagramme d’Espace-Temps : Visualiser le Relatif

Pour visualiser ce concept, les physiciens utilisent ce qu’on appelle un diagramme d’espace-temps. Imaginez un graphique où l’axe vertical représente le temps, et l’axe horizontal représente l’espace. Un objet immobile sera représenté par une ligne verticale (il reste à la même position dans l’espace au fil du temps), tandis qu’un objet en mouvement sera représenté par une ligne inclinée. Plus un objet se déplace rapidement, plus la ligne est proche de l’horizontale (la limite étant la ligne de la lumière, à 45°).

Dans ce diagramme, tous les événements dans l’univers sont représentés par des points dans ce plan, et la trajectoire d’un objet dans l’espace-temps est appelée sa « ligne d’univers ». Pour relier deux événements, on trace la distance de l’intervalle d’espace-temps, et c’est là que la contraction des longueurs et la dilatation du temps prennent tout leur sens. En effet, dans ce diagramme, les effets de la relativité deviennent visibles, et l’on voit pourquoi la simultanéité et la longueur dépendent du mouvement de l’observateur.

L’Espace-Temps : Un Univers Plus Flexible

L’espace-temps n’est pas rigide comme un échiquier géant ; il est « flexible ». Ce concept, encore difficile à concevoir pour l’époque d’Einstein, révolutionne la physique. Cela signifie qu’au lieu de penser l’univers comme un endroit où des objets bougent indépendamment du temps, nous devons imaginer un continuum espace-temps, où chaque objet suit une trajectoire unique et invariable.

La contraction des longueurs et la dilatation du temps sont donc des manifestations de la structure de l’espace-temps. Elles ne sont pas des illusions ; elles sont des conséquences naturelles d’un monde où l’espace et le temps sont intimement liés

Redéfinir la Simultanéité et Embrasser la Relativité : Un Nouveau Regard sur l’Univers

Avec l’espace et le temps fusionnés dans un seul espace-temps, nos concepts de longueur et de durée deviennent relatifs. Cette redéfinition radicale nous conduit à une conclusion surprenante : la simultanéité est elle-même relative.

Simultanéité Relative : Quand « En Même Temps » Dépend de Qui Regarde

Revenons à notre exemple des éclairs frappant un train en mouvement. Avant la théorie de la relativité, il semblait évident que deux événements pouvaient être observés « en même temps » par n’importe qui, qu’il soit dans le train ou sur le quai. Mais Einstein montre que cette intuition est fausse : pour que deux événements soient simultanés, il faut qu’ils soient observés par un même observateur dans un même référentiel.

La formule de transformation temporelle de Lorentz, que nous avons introduite plus tôt, décrit précisément pourquoi cela se produit. En fait, elle implique que le temps « vécu » par chaque observateur dépend de sa vitesse relative par rapport aux événements qu’il observe. En d’autres termes, la simultanéité d’événements dépend du point de vue de l’observateur.

Résumé des Transformations et leurs Effets

Avec les transformations de Lorentz, on comprend que :

  • Les longueurs se contractent dans le sens du mouvement : L = L_0 \sqrt{1 - \frac{v^2}{c^2}}.
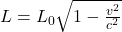  • Le temps se dilate pour les observateurs en mouvement relatif : \Delta t = \gamma , \Delta t_0.
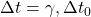  • La simultanéité devient relative, et les transformations nous permettent de passer d’un référentiel à un autre tout en conservant les mêmes lois de la physique.

Ces concepts révolutionnent notre manière de percevoir l’univers. Désormais, les observateurs en mouvement par rapport à un même objet ne s’accorderont pas sur la longueur de l’objet, la durée d’un événement, ou sur le fait que deux événements soient simultanés.

Les Applications Pratiques : De la Théorie à la Réalité

La relativité restreinte pourrait sembler abstraite, mais ses effets se manifestent dans des domaines de notre vie quotidienne. Voici quelques exemples :

  1. Les Particules à Haute Vitesse : Dans les accélérateurs de particules, les physiciens accélèrent des particules à des vitesses proches de celle de la lumière. Sans la dilatation du temps, ces particules se désintégreraient bien avant d’atteindre les détecteurs. La relativité explique pourquoi elles survivent plus longtemps lorsqu’elles sont observées à ces vitesses extrêmes.
  2. Les Systèmes de Navigation GPS : Les satellites GPS orbitent autour de la Terre à des vitesses élevées et sont soumis à une gravité moindre que celle de la surface terrestre. En raison de ces effets relativistes, leurs horloges se décalent par rapport aux horloges au sol. Les ingénieurs corrigent ces écarts en intégrant les effets de la dilatation du temps pour fournir des localisations précises.
  3. Les Rayons Cosmiques et les Muons : Les muons, des particules créées dans l’atmosphère par les rayons cosmiques, devraient normalement se désintégrer en microsecondes. Mais grâce à la dilatation du temps, ils « vivent » suffisamment longtemps pour atteindre la surface terrestre, offrant des preuves directes de la relativité.

La Relativité Restreinte : Une Invitation à Repenser le Réel

La relativité restreinte, en montrant que tout est relatif – les longueurs, les durées, et même la simultanéité – change notre compréhension de la nature de l’univers. Elle nous invite à voir l’espace et le temps comme unis dans un tout dynamique, et à comprendre que la réalité dépend du référentiel dans lequel nous nous trouvons. Nous vivons dans un univers où les notions classiques d’espace et de temps n’ont plus de sens absolu.

Et voilà, le voyage dans l’espace-temps touche à sa fin ! Nous avons exploré comment la contraction des longueurs, la dilatation du temps, et la relativité de la simultanéité sont intrinsèquement liées. Ces concepts, bien que déroutants, nous permettent de mieux comprendre le fonctionnement de notre univers – et ce n’est que le début, car la relativité générale d’Einstein ira encore plus loin en intégrant la gravité dans ce fabuleux espace-temps.

Check Also

Thermenwelt Bad Vilbel : Le futur éden aquatique d’Allemagne

Imaginez un lieu où le bien-être, le fun en famille et le sport se rencontrent, …

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *

© EYELO 2024, tout droit réservé