Cet article m’a été inspiré par une vidéo fascinante que j’ai découverte récemment sur YouTube. Intitulée « L’Équation du Temps », elle explore une complication horlogère qui illustre parfaitement à quel point le temps est bien plus qu’une simple succession de minutes et d’heures. Si vous n’avez pas encore vu cette vidéo, je vous recommande vivement de la regarder avant de plonger dans cet article, car elle explique en détail les principes fondamentaux de cette mystérieuse équation. Vous pouvez la retrouver ici : L’Équation du Temps – YouTube et en plus c’est une explication réalisée avec talent par Olivier Mory, un argument suplémentaire.
Intrigué par les mathématiques et la physique derrière cette équation, j’ai voulu pousser l’analyse plus loin. Ensemble, nous allons décortiquer les rouages mathématiques et astronomiques de l’équation du temps, en passant par les lois de Kepler, les subtilités de l’inclinaison terrestre, et même les mystères de la relativité. Le tout, bien sûr, avec une bonne dose d’humour et de curiosité scientifique !
Le Temps, une Illusion (Merci la Terre et son orbite en forme d’œuf)
Quand on pense au temps, on imagine quelque chose de simple : une journée dure 24 heures, une heure dure 60 minutes, et ainsi de suite. Mais ce que peu de gens savent, c’est que la Terre et le Soleil ont décidé de rendre les choses un peu plus compliquées. Pour nous, pauvres mortels, il est tentant de croire que le soleil est toujours à l’heure, mais en réalité, il passe son temps à arriver en avance ou en retard, parfois jusqu’à 16 minutes !
Mais d’où vient cette différence ? Tout commence avec la forme de l’orbite de la Terre, qui n’est pas parfaitement circulaire, mais elliptique (merci Kepler !). Et oui, notre planète préfère les œufs aux cercles parfaits. Cette forme d’ellipse implique que la vitesse à laquelle la Terre se déplace autour du Soleil varie en fonction de sa position.
Les lois de Kepler : L’ellipse au cœur du chaos temporel
Pour modéliser cette orbite, il nous faut plonger dans les lois de Kepler. La première loi nous dit que la Terre décrit une ellipse autour du Soleil, avec ce dernier situé à l’un des foyers de cette ellipse. Cette ellipse est définie par son excentricité ![]() , qui mesure à quel point l’orbite dévie d’un cercle parfait. Plus
, qui mesure à quel point l’orbite dévie d’un cercle parfait. Plus ![]() est grand, plus l’ellipse est allongée.
est grand, plus l’ellipse est allongée.
L’équation d’une ellipse est donnée par :
![]()
où :
 est le demi-grand axe (la distance du centre de l’ellipse au bord le plus éloigné),
est le demi-grand axe (la distance du centre de l’ellipse au bord le plus éloigné),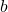 est le demi-petit axe (la distance du centre de l’ellipse au bord le plus proche).
est le demi-petit axe (la distance du centre de l’ellipse au bord le plus proche).
Mais les choses deviennent plus intéressantes (et complexes !) quand on parle de la position de la Terre à un instant donné. La vitesse de la Terre varie en fonction de sa distance au Soleil, et cela se traduit par des concepts d’anomalie excentrique ![]() et d’anomalie vraie
et d’anomalie vraie ![]() .
.
Anomalie excentrique : La clé de l’ellipse
L’anomalie excentrique ![]() est un angle qui relie la position de la Terre sur son orbite elliptique à un cercle imaginaire qui a le même centre et le même demi-grand axe que l’ellipse. Le calcul de
est un angle qui relie la position de la Terre sur son orbite elliptique à un cercle imaginaire qui a le même centre et le même demi-grand axe que l’ellipse. Le calcul de ![]() repose sur la fameuse équation de Kepler :
repose sur la fameuse équation de Kepler :
![]()
où :
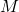 est l’anomalie moyenne, qui augmente de manière linéaire avec le temps,
est l’anomalie moyenne, qui augmente de manière linéaire avec le temps, 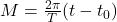 ,
, est l’excentricité de l’orbite,
est l’excentricité de l’orbite,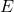 est l’anomalie excentrique.
est l’anomalie excentrique.
Cette équation est transcendante, c’est-à-dire qu’elle ne peut pas être résolue directement, mais nécessite des méthodes numériques d’approximation, comme la méthode de Newton-Raphson, pour obtenir ![]() .
.
Anomalie vraie : La position réelle de la Terre sur son orbite
Une fois que nous avons ![]() , nous pouvons calculer l’anomalie vraie
, nous pouvons calculer l’anomalie vraie ![]() , qui représente l’angle entre le Soleil, la Terre et le périhélie (le point où la Terre est la plus proche du Soleil). L’anomalie vraie est donnée par la relation suivante :
, qui représente l’angle entre le Soleil, la Terre et le périhélie (le point où la Terre est la plus proche du Soleil). L’anomalie vraie est donnée par la relation suivante :
![]()
Cette relation nous donne la position exacte de la Terre sur son orbite à un moment donné.
Pourquoi la vitesse de la Terre change ?
La deuxième loi de Kepler, également connue sous le nom de loi des aires, nous dit que la Terre balaie des aires égales en des temps égaux. Cela signifie qu’elle se déplace plus vite quand elle est près du Soleil (au périhélie) et plus lentement quand elle en est éloignée (à l’aphélie). Mathématiquement, cette loi se traduit par une conservation du moment angulaire, où la vitesse orbitale ![]() est donnée par :
est donnée par :
![]()
où :
 est le demi-grand axe,
est le demi-grand axe,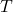 est la période de révolution,
est la période de révolution, est l’excentricité de l’orbite,
est l’excentricité de l’orbite,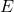 est l’anomalie excentrique.
est l’anomalie excentrique.
Cette variation de vitesse signifie que le temps solaire vrai (basé sur la position apparente du Soleil dans le ciel) diffère du temps solaire moyen (basé sur une journée de 24 heures constantes). C’est cette différence que l’équation du temps corrige.
Inclinaison et Ellipse : Le Duo Dynamique de l’Erreur de Temps
La variation de la vitesse de la Terre sur son orbite elliptique n’est pas la seule coupable des décalages entre l’heure solaire vraie et l’heure solaire moyenne. Un autre facteur important entre en jeu : l’inclinaison de l’axe de la Terre. Cet angle de 23,5 degrés par rapport à la perpendiculaire au plan de l’orbite terrestre (l’écliptique) est la raison pour laquelle nous avons des saisons, mais aussi pourquoi le temps solaire n’est pas constant tout au long de l’année.
Le mouvement apparent du Soleil sur l’écliptique
Pour comprendre l’impact de cette inclinaison, imaginons le mouvement apparent du Soleil sur la sphère céleste. La Terre étant inclinée, le Soleil ne se déplace pas toujours directement au-dessus de l’équateur céleste. Au lieu de cela, son parcours varie entre le tropique du Cancer (au nord) et le tropique du Capricorne (au sud), selon la période de l’année. Ce mouvement est donc oblique par rapport à l’équateur céleste, ce qui complique encore plus les calculs du temps solaire vrai.
Le Soleil se déplace à une vitesse apparente variable dans le ciel au cours de l’année, et l’angle sous lequel il est perçu depuis la Terre change constamment. Cette variation angulaire est directement liée à la projection de l’orbite terrestre sur le plan de l’équateur céleste.
Modélisation mathématique : latitude écliptique et longitude solaire
En mathématiques, cela revient à considérer la latitude écliptique ![]() et la longitude solaire
et la longitude solaire ![]() , qui décrivent la position apparente du Soleil sur la sphère céleste en fonction de l’inclinaison de l’axe de la Terre et de la progression de son orbite. Ces deux grandeurs sont liées par des relations trigonométriques complexes.
, qui décrivent la position apparente du Soleil sur la sphère céleste en fonction de l’inclinaison de l’axe de la Terre et de la progression de son orbite. Ces deux grandeurs sont liées par des relations trigonométriques complexes.
La latitude écliptique est souvent approximée par ![]() (car le Soleil reste proche du plan de l’écliptique), mais la longitude solaire est plus intéressante. Elle suit la relation suivante :
(car le Soleil reste proche du plan de l’écliptique), mais la longitude solaire est plus intéressante. Elle suit la relation suivante :
![]()
où :
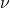 est l’anomalie vraie,
est l’anomalie vraie,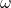 est l’argument du périhélie, qui est l’angle entre le périhélie et l’ascension droite de l’équinoxe de printemps.
est l’argument du périhélie, qui est l’angle entre le périhélie et l’ascension droite de l’équinoxe de printemps.
Le Soleil, dans sa course apparente, suit une trajectoire inclinée par rapport à l’équateur céleste. Cette inclinaison est modélisée par la relation suivante :
![]()
où :
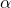 est l’ascension droite du Soleil (sa position angulaire sur l’équateur céleste),
est l’ascension droite du Soleil (sa position angulaire sur l’équateur céleste), est l’inclinaison de l’axe terrestre (environ 23,5°),
est l’inclinaison de l’axe terrestre (environ 23,5°),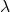 est la longitude solaire.
est la longitude solaire.
Cette relation explique comment l’inclinaison de l’axe de la Terre déplace la position apparente du Soleil dans le ciel, et, par conséquent, modifie le temps que prend le Soleil à atteindre le méridien chaque jour. Cela ajoute une autre variation au temps solaire vrai.
Effet de l’inclinaison sur l’équation du temps
La combinaison de cette inclinaison avec l’orbite elliptique de la Terre fait que la durée entre deux passages consécutifs du Soleil au méridien (le point où le Soleil est à son zénith) varie tout au long de l’année. L’inclinaison de l’axe terrestre introduit une variation supplémentaire d’environ 9 à 10 minutes dans l’équation du temps, qui vient s’ajouter à celle due à l’excentricité de l’orbite.
Le décalage causé par l’inclinaison est modélisé par un terme supplémentaire dans l’équation du temps :
![]()
où :
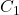 est une constante qui dépend de l’inclinaison de l’axe terrestre,
est une constante qui dépend de l’inclinaison de l’axe terrestre,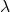 est la longitude solaire.
est la longitude solaire.
Ce terme vient s’ajouter au terme dû à l’excentricité de l’orbite, pour donner l’équation complète de la variation temporelle entre le temps solaire vrai et le temps solaire moyen.
Formules aux Petits Oignons : La Trigo qui Fait Tourner la Terre
Nous avons vu que l’orbite elliptique de la Terre et l’inclinaison de son axe introduisent chacun une variation dans le temps solaire vrai par rapport au temps solaire moyen. Maintenant, il est temps de combiner ces deux effets pour obtenir l’équation du temps complète, cette fameuse formule qui nous dit de combien de minutes le Soleil est en avance ou en retard à différents moments de l’année.
La contribution de l’excentricité de l’orbite
L’effet de l’orbite elliptique se traduit par une variation de la vitesse apparente du Soleil dans le ciel. Cet effet peut être modélisé par un premier terme dans l’équation du temps, qui est proportionnel à l’excentricité de l’orbite et à la variation angulaire du Soleil. Ce terme prend la forme :
![]()
où :
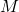 est l’anomalie moyenne, qui augmente de manière linéaire au fil des jours,
est l’anomalie moyenne, qui augmente de manière linéaire au fil des jours,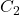 est une constante proportionnelle à l’excentricité de l’orbite
est une constante proportionnelle à l’excentricité de l’orbite  .
.
Comme l’anomalie moyenne ![]() croît linéairement avec le temps, ce terme introduit une variation périodique qui cause des différences entre le temps solaire vrai et le temps solaire moyen tout au long de l’année.
croît linéairement avec le temps, ce terme introduit une variation périodique qui cause des différences entre le temps solaire vrai et le temps solaire moyen tout au long de l’année.
La contribution de l’inclinaison de l’axe terrestre
L’inclinaison de l’axe terrestre, comme nous l’avons vu, modifie également la position apparente du Soleil dans le ciel. Cela crée une variation supplémentaire dans le temps solaire vrai, qui est modélisée par un deuxième terme dans l’équation du temps :
![]()
où :
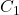 est une constante liée à l’inclinaison de l’axe terrestre,
est une constante liée à l’inclinaison de l’axe terrestre,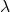 est la longitude solaire.
est la longitude solaire.
L’équation complète du temps
Nous sommes enfin prêts à assembler ces deux termes. L’équation du temps complète est donnée par la somme des contributions dues à l’excentricité de l’orbite et à l’inclinaison de l’axe :
![]()
Cette formule donne la différence entre le temps solaire vrai et le temps solaire moyen pour n’importe quel jour de l’année. Ce décalage varie entre environ +16 minutes (lorsque le Soleil est « en avance ») et -14 minutes (lorsqu’il est « en retard »). Ces variations se produisent de manière cyclique, atteignant des extrêmes aux alentours du début du mois de novembre (retard maximal) et du mois de février (avance maximale).
Une approche plus précise : la vraie équation du temps
Si on souhaite affiner cette équation, il est possible d’ajouter d’autres termes pour mieux modéliser les effets subtils de la dynamique orbitale. L’équation du temps peut être écrite avec une plus grande précision comme suit :
![]()
où :
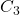 et
et 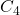 sont des coefficients supplémentaires qui prennent en compte des effets secondaires comme les termes de deuxième ordre dans le développement trigonométrique.
sont des coefficients supplémentaires qui prennent en compte des effets secondaires comme les termes de deuxième ordre dans le développement trigonométrique.
Cette version plus précise de l’équation est celle utilisée dans les calculs astronomiques et les montres haut de gamme qui affichent l’équation du temps. Ces termes supplémentaires permettent de corriger avec plus de précision les variations du temps solaire vrai, offrant ainsi un modèle très précis de la position apparente du Soleil tout au long de l’année.
Visualisation des variations : une sinusoïde double
Si nous traçons cette équation au fil des jours de l’année, nous obtenons une courbe en forme de double sinusoïde, où le décalage entre le temps solaire vrai et le temps solaire moyen oscille tout au long de l’année.
La courbe ressemble à ceci :
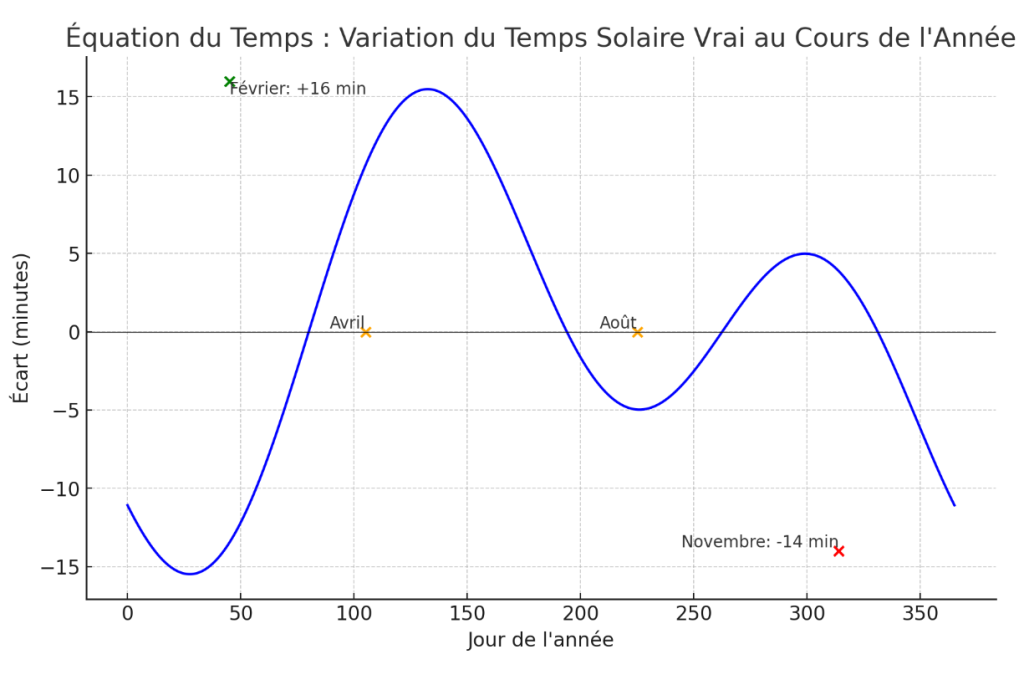
- Au mois de novembre, l’écart atteint environ -14 minutes (le Soleil est en retard).
- Au mois de février, il atteint environ +16 minutes (le Soleil est en avance).
- En avril et août, les deux courbes se croisent, et le temps solaire vrai et moyen coïncident.
La forme de cette courbe est le résultat de l’interaction entre les deux phénomènes : la variation de la vitesse due à l’orbite elliptique et la modification angulaire due à l’inclinaison de l’axe terrestre.
Le Défi des Horlogers : Réduire Tout ça en Quelques Rouages
Après avoir exploré les méandres mathématiques de l’équation du temps, on pourrait se demander : comment diable une montre mécanique peut-elle afficher une telle variation avec seulement des engrenages et des ressorts ? Les horlogers sont de véritables magiciens des rouages, et intégrer l’équation du temps dans une montre est l’un des sommets de leur art.
Qu’est-ce qu’une montre à équation du temps ?
Une montre équipée de la complication de l’équation du temps est capable de montrer, en plus de l’heure solaire moyenne, l’écart entre le temps solaire vrai et le temps civil. En pratique, cela se traduit souvent par une aiguille supplémentaire sur le cadran ou un affichage séparé qui indique l’avance ou le retard du soleil à un moment donné de l’année.
Pour comprendre comment cela fonctionne, il faut se plonger dans la mécanique de la montre. Mais attention, les montres à équation du temps ne sont pas des montres comme les autres : elles embarquent une mécanique aussi précise qu’ingénieuse.
Comment convertir des équations en rouages ?
La principale difficulté pour les horlogers est de traduire des équations trigonométriques en mouvements mécaniques. Ils doivent reproduire la double sinusoïde que nous avons vue précédemment, avec des variations de l’ordre de quelques minutes, et cela en utilisant uniquement des engrenages et des leviers.
Le mécanisme fonctionne généralement à l’aide de cames. Les cames sont des pièces mécaniques qui, lorsqu’elles tournent, modifient la position d’un levier ou d’une autre pièce de manière non linéaire. Voici comment cela fonctionne dans une montre à équation du temps :
- Came annuelle : Une came spéciale, appelée came annuelle, est découpée pour reproduire la double sinusoïde de l’équation du temps. Cette came tourne une fois par an et est calée sur le calendrier grégorien de la montre. Sa forme irrégulière permet de traduire l’oscillation entre l’avance et le retard du Soleil.
- Levier suiveur : Un levier est en contact constant avec la came. Au fur et à mesure que la came tourne, le levier suit sa forme. Ce mouvement est ensuite transmis à une aiguille ou à un affichage de l’équation du temps.
Pourquoi tout ça est si difficile ?
La précision requise pour tailler la came est l’un des défis les plus importants. Elle doit être taillée avec une grande minutie pour refléter exactement la forme de la courbe de l’équation du temps. Le moindre écart pourrait entraîner des erreurs de plusieurs secondes, voire minutes, dans l’affichage.
De plus, cette mécanique doit être intégrée dans une montre déjà complexe, qui comprend souvent d’autres complications comme les phases de lune, les calendriers perpétuels, ou même des répétitions minutes. Chaque complication supplémentaire augmente la complexité et les défis de miniaturisation.
L’épure mathématique derrière la came
Mathématiquement, le profil de la came est dérivé directement de l’équation du temps. La forme de la came doit refléter la variation décrite par l’équation :
![]()
Le rôle de la came est donc de convertir ces variations temporelles en variations spatiales, où la position angulaire de la came correspond à un jour donné de l’année, et le déplacement vertical du levier est proportionnel au décalage temporel entre le temps solaire vrai et le temps solaire moyen.
Pour obtenir cette forme, les horlogers travaillent en étroite collaboration avec des mathématiciens et des ingénieurs pour créer une épure précise, une sorte de schéma mathématique et géométrique de la came, avant de la tailler avec une extrême précision.
Des exemples célèbres de montres à équation du temps
Certaines maisons horlogères célèbres se sont aventurées dans la fabrication de montres à équation du temps. Voici quelques exemples notables :
- Breguet Marine Équation Marchante 5887 : Cette montre affiche non seulement l’équation du temps, mais intègre également un calendrier perpétuel et une répétition minutes. Le niveau de finition de la came et de ses composants mécaniques est tout simplement exceptionnel.
- Vacheron Constantin Patrimony Traditionnelle Équation du Temps : Cette montre est un exemple magnifique de la manière dont les horlogers parviennent à intégrer la complexité de l’équation du temps tout en maintenant une esthétique élégante et minimaliste.
Pourquoi les montres à équation du temps sont rares ?
Outre la complexité technique et la précision nécessaire pour réaliser une montre à équation du temps, ces montres restent rares en raison de leur faible utilité pratique. Dans un monde moderne où la majorité des gens se fient aux horloges atomiques et aux smartphones pour connaître l’heure exacte, l’équation du temps est une complication de pur prestige. Elle fascine par son défi technique et son lien intime avec l’astronomie.
Maths, Physique et Philosophie : Qui Décide Vraiment de l’Heure ?
Maintenant que nous avons exploré les aspects techniques et horlogers de l’équation du temps, il est temps de prendre un peu de recul et de nous poser une question plus profonde : qu’est-ce que le temps, exactement ? Comment la mathématique, la physique, et même notre perception influencent la manière dont nous mesurons cette dimension fondamentale ?
Le temps, une construction humaine ?
On pourrait dire que le temps tel que nous le connaissons est une construction humaine. L’idée d’une journée de 24 heures, chaque heure divisée en 60 minutes, n’est rien d’autre qu’une convention. Cette division arbitraire est née de la nécessité de structurer nos journées, de synchroniser nos activités avec le cycle solaire. Mais est-ce vraiment ce qu’est le temps ?
Du point de vue des mathématiques, le temps est souvent traité comme une variable dans les équations, une grandeur abstraite qui évolue de manière linéaire. En physique, il est une dimension intrinsèque de l’univers, inséparable de l’espace. Dans le modèle de la relativité restreinte d’Einstein, le temps devient une composante du continuum espace-temps, où il peut être dilaté ou contracté en fonction de la vitesse à laquelle on se déplace. Les horloges elles-mêmes, en orbite ou sur Terre, ne mesurent donc pas exactement la même durée.
Le Soleil en retard ou en avance ? Une illusion cosmique
Lorsque nous parlons de l’équation du temps, nous décrivons une illusion qui résulte des mouvements complexes de la Terre. En réalité, ni le Soleil ni la Terre ne sont « en avance » ou « en retard » ; c’est notre convention humaine qui est mise à mal par les caprices de l’orbite elliptique et de l’inclinaison de l’axe terrestre.
Les mathématiques nous montrent que le temps solaire vrai, c’est-à-dire le temps réel qu’il faut au Soleil pour revenir à la même position dans le ciel, n’est pas constant. Mais cette variation est imperceptible pour nous au quotidien. Pourtant, il suffit de jeter un coup d’œil à une montre mécanique équipée de l’équation du temps pour réaliser à quel point notre conception du temps est simplifiée.
Temps et relativité : Et si nous avions tort depuis le début ?
En physique moderne, le temps est bien plus qu’une simple succession de secondes, minutes et heures. Dans le cadre de la théorie de la relativité générale, formulée par Einstein, le temps et l’espace sont liés de façon indissociable. Un objet massif comme la Terre courbe l’espace autour de lui, et cette courbure affecte également l’écoulement du temps. Plus précisément, le temps se dilate en présence d’un champ gravitationnel intense.
Cela signifie qu’une horloge placée à la surface de la Terre fonctionne légèrement plus lentement qu’une horloge en orbite. Cette dilatation du temps est une conséquence directe de l’équation d’Einstein :
![]()
où :
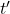 est le temps mesuré par une horloge près d’un objet massif,
est le temps mesuré par une horloge près d’un objet massif,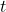 est le temps mesuré loin de cet objet,
est le temps mesuré loin de cet objet,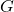 est la constante gravitationnelle,
est la constante gravitationnelle,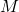 est la masse de l’objet (la Terre, par exemple),
est la masse de l’objet (la Terre, par exemple), est la distance au centre de l’objet,
est la distance au centre de l’objet, est la vitesse de la lumière.
est la vitesse de la lumière.
À l’échelle humaine, cette différence est infime, mais elle devient notable pour les systèmes de haute précision comme le GPS, qui doit corriger en permanence les effets relativistes pour donner une position exacte.
Le paradoxe des horloges : Quelle heure est-il, vraiment ?
Finalement, la question se pose : qui décide vraiment de l’heure ? Est-ce la Terre, qui suit ses propres lois orbitales ? Est-ce notre société, qui impose un découpage arbitraire du temps ? Ou est-ce la physique, qui nous montre que le temps n’est pas absolu et peut être modifié en fonction des conditions de l’espace environnant ?
L’équation du temps, tout en étant une curiosité horlogère fascinante, nous rappelle que le temps lui-même est bien plus mystérieux et complexe que ce que nos montres, aussi précises soient-elles, peuvent indiquer. Et comme l’a si bien dit Einstein, « Le temps est une illusion, mais une illusion bien tenace. »
Conclusion : Et Maintenant, Quelle Heure Est-il Vraiment ?
Après tout ce voyage à travers les orbites elliptiques, les lois de Kepler, l’inclinaison terrestre et même la relativité générale, on peut se demander une dernière fois : mais quelle heure est-il vraiment ?
D’un côté, il y a nos horloges qui battent mécaniquement au rythme de secondes parfaitement égales, jour après jour, comme si de rien n’était. De l’autre, il y a l’univers, ce farceur cosmique, qui s’amuse à jouer avec notre perception du temps. Le Soleil arrive tantôt en avance, tantôt en retard, et la Terre, dans sa course irrégulière autour du Soleil, modifie subtilement l’écoulement du temps. Et si ça ne suffisait pas, la relativité d’Einstein nous rappelle que même nos montres ne mesurent pas le même temps selon où elles se trouvent.
Alors, quelle heure est-il ? La réponse est simple : ça dépend. Ça dépend de votre position sur la Terre, de la date du calendrier, et même de la hauteur à laquelle vous vous trouvez. Peut-être que ce qu’il nous reste de plus fiable, ce sont les équations. L’équation du temps nous dit avec précision combien de minutes le Soleil est « en avance » ou « en retard », mais cela reste une illusion de plus.
En fin de compte, l’heure est une invention humaine, une convention pratique pour organiser nos vies. Mais sous cette apparente simplicité, la mécanique céleste et la relativité physique nous rappellent que le temps est une bête beaucoup plus complexe à dompter. Alors la prochaine fois que vous regarderez votre montre, pensez à tout cela : une petite révolution elliptique, une pincée d’inclinaison terrestre, et une bonne dose de mathématiques rendent votre minute si précise… ou pas !
 Pourton.info
Pourton.info 



