Décryptage du Modèle Standard : Ou comment les particules jouent à cache-cache avec la physique

21 septembre 2024 Actualité, Physique, Science et Techologie

Introduction : Le monstre mathématique du Modèle Standard

Lorsque j’ai vu cette formule pour la première fois, mon cerveau a fait une petite pause. C’était comme contempler un labyrinthe de symboles, de dérivées et d’interactions qui semblaient tous se répondre. Et puis, à y regarder de plus près, j’ai réalisé que ce n’était pas n’importe quelle équation. Ce que vous voyez ici, c’est une version ultra-détaillée du Lagrangien du Modèle Standard.

Ce Lagrangien, c’est un peu comme une encyclopédie mathématique qui compile toutes les interactions entre les particules et les forces fondamentales de la nature. Mais ne vous inquiétez pas, nous allons plonger dans les détails ensemble. Voici la formule complète pour les plus aventureux :

Cette équation n’est pas qu’un simple exercice d’esthétisme mathématique. Elle décrit littéralement presque tout ce que nous savons sur la physique des particules. Des gluons aux bosons W et Z, en passant par le mystérieux boson de Higgs, chaque terme de cette équation raconte une histoire fascinante.

Mais qu’est-ce que tout cela signifie vraiment ? C’est en me posant cette question que j’ai eu l’idée d’écrire cet article. Dans les chapitres qui suivent, je vais vous emmener dans une exploration guidée de cette équation monstrueuse, en décomposant chaque partie pour la rendre plus digeste. Car au fond, ce qui semble être un amas de symboles est en réalité une carte très précise des règles qui régissent l’univers.

Chapitre 1 : « Un modèle pas si standard que ça »

Le Modèle Standard a peut-être un nom modeste, mais en réalité, c’est une des théories les plus fondamentales et complètes de la physique moderne. Il regroupe trois des quatre forces fondamentales de la nature (la force électromagnétique, la force faible et la force forte), ainsi que toutes les particules qui interagissent avec elles. C’est un peu comme si on avait trouvé la recette ultime pour décrire l’univers… enfin, presque.

Le Modèle Standard se base sur des symétries spécifiques qui décrivent comment les particules interagissent entre elles. Ces symétries sont représentées par des groupes de Lie, notés en SU(3)_C \times SU(2)_L \times U(1)_Y. Ces groupes sont comme les règles d’un jeu très complexe, et les particules doivent suivre ces règles pour se comporter correctement.

Alors, pourquoi un « modèle standard » ? Il s’avère que ce modèle fonctionne si bien pour expliquer les particules et les forces que les physiciens ont dû mal à l’appeler autrement. C’est un peu comme appeler la Tour Eiffel « un grand poteau de métal ». Ça sous-estime clairement l’ampleur de ce qu’il décrit.

Le Lagrangien : La recette en une formule

Le Modèle Standard peut être résumé dans une seule équation massive, sous une forme appelée Lagrangien. Ce dernier est un outil mathématique permettant de décrire la dynamique des systèmes physiques. Il intègre toutes les interactions entre les particules et les forces, dans une expression ultra-compacte (mais très compliquée). Le Lagrangien permet de décrire un système en termes d’énergie cinétique et potentielle, et peut être utilisé pour déterminer l’évolution dans le temps de n’importe quel système.

Voici une représentation générale du Lagrangien du Modèle Standard :

\mathcal{L}<em>{SM} = -\frac{1}{4} G</em>{\mu\nu}^a G^{a\mu\nu} - \frac{1}{4} W_{\mu\nu}^i W^{i\mu\nu} - \frac{1}{4} B_{\mu\nu} B^{\mu\nu} + \left( D_{\mu} \phi \right)^\dagger \left( D^{\mu} \phi \right) - V(\phi) + \mathcal{L}<em>{\text{fermions}} + \mathcal{L}</em>{\text{Yukawa}}

Cette équation peut sembler cryptique, mais ne t’inquiète pas, on va la décortiquer au fur et à mesure dans les chapitres suivants. Chaque terme correspond à une interaction spécifique entre les particules, et chaque symbole a sa propre signification.

C’est un peu comme si chaque terme de l’équation était une saveur différente dans une recette universelle. Certaines interactions concernent des particules comme les gluons, d’autres les bosons, et d’autres encore décrivent comment les fermions (comme les électrons) interagissent avec ces forces.

Symétries et particules

Les symétries du Modèle Standard sont cruciales pour comprendre pourquoi les particules agissent comme elles le font. Prenons les groupes SU(3)_C, SU(2)_L et U(1)_Y comme exemples :

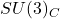  • SU(3)_C décrit l’interaction forte, qui est responsable de la cohésion des quarks au sein des protons et des neutrons. Cette force est transportée par des particules appelées gluons.
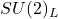  • SU(2)_L concerne la force faible, celle qui est impliquée dans les processus comme la désintégration radioactive. Les bosons W et Z en sont les transporteurs.
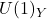  • U(1)_Y est lié à l’interaction électromagnétique, bien connue pour sa capacité à attirer les objets métalliques avec un aimant. Son transporteur est le photon.

À travers ces symétries, le Modèle Standard nous permet de comprendre pourquoi certaines particules interagissent entre elles, et d’autres non.

Chapitre 2 : « Gluons : Ces messagers à la charge colorée qui maintiennent l’univers collé »

Dans le cadre du Modèle Standard, les gluons sont les véritables ouvriers de l’univers. Leur rôle est de transporter la force forte, celle qui lie les quarks entre eux pour former des particules comme les protons et les neutrons. On peut donc les imaginer comme des sortes de « colle » qui maintient ensemble les composants fondamentaux de la matière.

Les gluons sont des bosons, des particules qui transmettent des forces, et ils sont uniques parce qu’ils transportent une charge particulière appelée charge de couleur. Mais attention, ne te laisse pas tromper par le nom ! Les « couleurs » des gluons n’ont rien à voir avec le spectre visible de la lumière. Il s’agit ici d’une analogie utilisée pour représenter les types d’interactions dans la force forte. Il y a trois types de charges de couleur : rouge, vert et bleu, mais ce ne sont que des noms pratiques pour faciliter la compréhension.

La force forte est gouvernée par le groupe de symétrie SU(3)_C, et les gluons, qui sont les transporteurs de cette force, interagissent entre eux en raison de cette symétrie. C’est un peu comme si les facteurs (les gluons) non seulement livraient des colis (les forces), mais prenaient aussi le temps de discuter entre eux au passage !

Le terme gluonique dans le Lagrangien

Dans le Lagrangien du Modèle Standard, les gluons et la force forte sont représentés par un terme spécifique. Le voici :

-\frac{1}{4} G_{\mu\nu}^a G^{a\mu\nu}

Dans cette expression, G_{\mu\nu}^a représente le champ de force gluonique, et l’indice a varie de 1 à 8, car il y a huit types de gluons différents. Le champ G_{\mu\nu}^a est une mesure de la force que le champ gluonique exerce dans l’espace-temps.

Le terme -\frac{1}{4} G_{\mu\nu}^a G^{a\mu\nu} est une manière concise de décrire l’énergie contenue dans ce champ, ainsi que les interactions entre les gluons eux-mêmes. C’est cette auto-interaction des gluons qui rend la force forte si particulière, et si « forte » justement.

Une force impossible à contenir

Contrairement aux autres forces, comme l’électromagnétisme, la force forte ne faiblit pas avec la distance. En fait, elle devient plus forte à mesure que les quarks s’éloignent les uns des autres. C’est un peu comme si un élastique invisible se tendait toujours plus à mesure qu’on essayait de séparer les quarks.

Cela conduit à un phénomène appelé confinement : il est impossible de trouver un quark isolé dans la nature. Si tu essaies de séparer un proton en ses quarks constitutifs, l’énergie que tu injectes dans ce processus se transforme en nouvelles paires de quarks et d’antiquarks. C’est comme si, en tirant trop fort sur un élastique, tu créais un nouvel élastique à partir de l’énergie que tu y mets.

Huit gluons, mais pourquoi pas plus ou moins ?

Les huit types de gluons correspondent aux différentes manières dont les charges de couleur peuvent interagir entre elles. Les gluons sont des combinaisons de paires de couleurs et d’anti-couleurs, comme rouge-antirouge ou bleu-antivert. Il existe huit combinaisons indépendantes, ce qui explique pourquoi nous avons huit gluons différents.

Un petit jeu amusant est d’essayer d’imaginer des gluons avec des couleurs visibles. Ça deviendrait vite un spectacle de feux d’artifice, avec des explosions de lumière colorée à chaque interaction de quarks !

Chapitre 3 : « Bosons : Les facteurs de l’univers qui livrent la force à domicile »

Les bosons sont comme des facteurs interstellaires. Ils livrent les forces fondamentales de la nature aux particules qui en ont besoin, un peu comme un service postal cosmique hyper-efficace. Dans le Modèle Standard, nous avons plusieurs types de bosons, chacun responsable de livrer une force spécifique.

Les bosons que nous allons examiner dans ce chapitre sont les bosons W et Z, qui transportent la force faible. Ils sont un peu moins connus que le photon (qui s’occupe de la force électromagnétique) ou les gluons (qui transportent la force forte), mais leur rôle est crucial. La force faible est responsable de processus comme la désintégration radioactive et de nombreux phénomènes subatomiques importants.

Le terme des bosons W et Z dans le Lagrangien

Le Lagrangien du Modèle Standard inclut un terme qui décrit les interactions des bosons W et Z. Voici à quoi cela ressemble :

-\frac{1}{4} W_{\mu\nu}^i W^{i\mu\nu} - \frac{1}{4} B_{\mu\nu} B^{\mu\nu}

Dans cette expression, W_{\mu\nu}^i représente le champ associé aux bosons W, tandis que B_{\mu\nu} est le champ pour le boson Z (qui est en fait une combinaison du champ B et du champ W après la brisure de symétrie électrofaible, mais on va y venir plus tard).

Ces termes sont similaires à ceux que nous avons vus pour les gluons dans le chapitre précédent. Ils mesurent l’énergie contenue dans les champs des bosons W et Z et comment ces bosons interagissent entre eux. Comme pour les gluons, cela inclut aussi les auto-interactions des bosons, une propriété qui leur permet de se livrer eux-mêmes des forces tout en interagissant avec les autres particules.

Force faible : Pourquoi « faible » ?

On pourrait penser que la force faible est un peu la « force oubliée », vu qu’elle porte ce nom peu flatteur. Mais ne te laisse pas tromper. Bien que son influence soit effectivement plus courte portée que celle de la force électromagnétique ou de la force forte, la force faible joue un rôle essentiel dans la transformation des particules.

Les bosons W et Z sont très lourds pour des particules élémentaires, et c’est cette masse élevée qui explique pourquoi la force faible agit sur des distances extrêmement courtes. Si tu t’éloignes trop des particules qui interagissent par la force faible, ces bosons deviennent trop massifs pour maintenir l’interaction. C’est un peu comme si un facteur devait transporter un colis tellement lourd qu’il ne pourrait le livrer qu’à une maison à côté.

Le boson Z : Le « mystère » de la neutralité

Le boson Z est neutre en charge électrique, mais il est lourd, tout comme son cousin le boson W. Il participe à des processus comme la diffusion de neutrinos, où il permet à ces particules fantomatiques d’interagir très légèrement avec la matière ordinaire.

Mais le rôle du boson Z ne s’arrête pas là : il est également impliqué dans la symétrie électrofaible, qui unifie la force faible et l’électromagnétisme à haute énergie. Cette symétrie se brise à basse énergie (comme celle à laquelle nous vivons), et c’est ce processus qui donne leur masse aux bosons W et Z.

Le facteur secret : La brisure de symétrie électrofaible

Les bosons W et Z n’existeraient pas tels que nous les connaissons sans un phénomène appelé brisure spontanée de symétrie. À très haute énergie, la force faible et l’électromagnétisme sont en fait deux aspects d’une seule et même force. Mais lorsque l’univers refroidit après le Big Bang, cette symétrie se brise. Le résultat ? Les bosons W et Z acquièrent leur masse, tandis que le photon reste sans masse et continue de transporter la force électromagnétique à longue portée.

Ce processus est gouverné par le fameux mécanisme de Higgs, dont nous parlerons plus en détail dans les chapitres à venir. Mais pour l’instant, retiens que sans la brisure de symétrie, notre univers serait bien différent – sans désintégration radioactive et sans forces faibles pour transformer les particules.

Chapitre 4 : « La faiblesse a du bon : Comment la force faible décape les particules »

La force faible est l’une des quatre forces fondamentales de la nature, mais elle se distingue par sa capacité à faire « changer » les particules. Elle est à l’origine de nombreux processus cruciaux dans l’univers, comme la désintégration radioactive. Contrairement à son nom peu flatteur, la force faible a un impact majeur sur la structure de la matière. C’est grâce à elle que les particules plus lourdes peuvent se transformer en particules plus légères, un processus essentiel pour des phénomènes comme la fusion nucléaire dans les étoiles.

Le terme de la force faible dans le Lagrangien

Dans le Lagrangien du Modèle Standard, les interactions de la force faible avec les particules de matière sont décrites par des termes spécifiques. Ces interactions impliquent les bosons W et Z, que nous avons déjà rencontrés, ainsi que les fermions (les particules de matière comme les quarks et les leptons).

Voici à quoi ressemble cette partie du Lagrangien :

\mathcal{L}<em>{\text{faible}} = \bar{\psi}<em>L \gamma^\mu \left( i \partial</em>\mu - g W</em>\mu^i T^i - g' B_\mu Y \right) \psi_L

Dans cette expression :

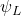  • \psi_L représente les fermions gauches (les particules de matière qui interagissent via la force faible),
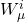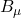  • W_\mu^i et B_\mu sont les champs des bosons W et Z,
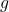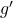  • g et g' sont des constantes de couplage qui mesurent la force de ces interactions.

Cette partie de l’équation décrit comment les particules comme les électrons ou les quarks interagissent avec les bosons W et Z via la force faible. Elle est cruciale pour comprendre pourquoi les particules se désintègrent ou se transforment en d’autres types de particules.

Désintégration et interaction

La force faible est responsable de la désintégration des particules lourdes. Par exemple, un neutron (composé de quarks) peut se transformer en proton, électron et neutrino via une interaction faible. C’est un processus essentiel pour la radioactivité, notamment la désintégration bêta, qui joue un rôle fondamental dans des phénomènes comme la fusion nucléaire au cœur des étoiles.

La désintégration se produit grâce à l’interaction entre les bosons W et Z et les fermions. Lorsqu’une particule comme un neutron se désintègre, un quark à l’intérieur change de type (ou « flavor ») en émettant un boson W. Ce boson se désintègre ensuite en un électron et un neutrino. Voilà comment la force faible fait « décaper » une particule plus lourde pour en créer une plus légère.

L’effet du champ de Higgs

Ce processus d’interaction est également lié au champ de Higgs, qui confère leur masse aux particules. La brisure de symétrie électrofaible, dont nous avons parlé plus tôt, permet à certains fermions d’acquérir une masse en interagissant avec le champ de Higgs. Sans cette interaction, les particules ne pourraient pas se désintégrer de cette manière.

Le champ de Higgs intervient dans cette équation par un terme supplémentaire qui décrit comment les fermions interagissent avec le boson de Higgs. Voici à quoi ressemble ce terme dans le Lagrangien :

\mathcal{L}_{\text{Yukawa}} = - y_f \bar{\psi}_L \phi \psi_R + \text{h.c.}

Dans cette expression, y_f est le couplage de Yukawa, qui mesure la force de l’interaction entre les fermions et le champ de Higgs. Le champ \phi représente le champ de Higgs.

C’est ce couplage qui donne leur masse aux fermions et permet à des particules comme les quarks de changer de type via la désintégration. Sans le couplage de Yukawa, les particules seraient sans masse et la force faible ne fonctionnerait pas comme nous la connaissons.

La surprise des neutrinos

Cependant, il y a un petit hic dans cette partie du Modèle Standard : elle postule que les neutrinos n’ont pas de masse. Ce que nous savons aujourd’hui, c’est que les neutrinos ont bel et bien une masse, bien que très petite. Cela constitue une des grandes énigmes non résolues du Modèle Standard, et une preuve que cette théorie, aussi élégante soit-elle, n’est pas complète.

Chapitre 5 : « Les fantômes de Higgs et autres petits esprits farceurs »

Dans l’univers mathématique du Modèle Standard, il existe des entités étranges appelées particules fantômes ou simplement fantômes. Mais ne t’inquiète pas, il ne s’agit pas de vrais esprits qui hantent les particules. Ces « fantômes » sont des artefacts mathématiques, nécessaires pour résoudre certaines incohérences dans les calculs. Ils ne se manifestent pas physiquement, mais sans eux, les équations deviendraient bien plus compliquées et, en fait, impraticables.

L’idée des fantômes est liée à la symétrie de jauge du Modèle Standard, en particulier lors des tentatives de renormalisation des théories des champs quantiques. Lorsque les théoriciens veulent nettoyer les redondances des équations dans les interactions des champs de jauge (comme les bosons W et Z), ces fantômes apparaissent pour aider à maintenir la cohérence mathématique. C’est un peu comme des éboueurs invisibles qui nettoient derrière la scène.

Le rôle des fantômes dans le Lagrangien

Dans le Lagrangien du Modèle Standard, les fantômes interviennent dans les calculs associés aux champs de jauge. Ils servent à annuler certaines redondances dues à la symétrie de jauge, un problème appelé la fixation de jauge. Voici un exemple d’un terme qui fait intervenir les fantômes dans le Lagrangien :

\mathcal{L}<em>{\text{ghost}} = - \bar{c}^a \left( \partial^\mu D</em>\mu^{ab} \right) c^b

Dans cette expression :

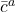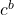  • \bar{c}^a et c^b représentent les champs des fantômes de Faddeev-Popov, qui annulent les redondances dans les interactions de la force faible,
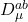  • D_\mu^{ab} est le champ covariant qui décrit comment les fantômes interagissent avec les autres particules.

Ces fantômes, bien qu’ils soient mathématiquement nécessaires, n’apparaissent jamais dans les résultats physiques des expériences. Leur seule fonction est de simplifier les calculs dans certaines théories des champs quantiques. C’est un peu comme si ces fantômes s’assuraient que tout se passe bien en arrière-plan, sans jamais se montrer sur la scène principale.

Fantômes et le mécanisme de Higgs

Les fantômes jouent également un rôle dans le mécanisme de Higgs, où ils aident à annuler les termes qui deviennent trop compliqués à gérer dans les calculs. Le champ de Higgs est un champ scalaire qui interagit avec les autres champs du Modèle Standard, et les fantômes apparaissent dans ce cadre pour faciliter ces interactions.

Lorsque la symétrie électrofaible se brise, créant le boson de Higgs et donnant de la masse aux bosons W et Z, les fantômes sont là pour nettoyer les termes qui pourraient causer des incohérences dans les équations. C’est une des raisons pour lesquelles on parle souvent des fantômes dans les théories de jauge comme d’un mécanisme de « nettoyage » des termes indésirables.

Des fantômes inoffensifs

Bien qu’ils soient invisibles dans les résultats des expériences, les fantômes sont essentiels pour assurer la cohérence mathématique du Modèle Standard. Sans eux, les théories des champs quantiques seraient truffées de problèmes, et nos équations seraient inutilisables. Ils ne violent pas les règles de la physique, car ils ne sont pas des particules physiques ; ils sont uniquement une astuce mathématique.

Cela dit, ces petits esprits farceurs ne seront jamais détectés dans un accélérateur de particules comme le LHC (Large Hadron Collider), mais ils existent dans le royaume des mathématiques pour une bonne raison. C’est leur absence des résultats physiques qui fait d’eux des fantômes, des entités purement théoriques qui se contentent de faire leur travail en coulisses.

Chapitre 6 : « Les fantômes de Faddeev-Popov : Nettoyeurs mathématiques invisibles »

Après avoir rencontré les premiers fantômes, il est temps de parler des plus célèbres d’entre eux : les fantômes de Faddeev-Popov. Si tu es un peu surpris par la fréquence des « fantômes » dans le Modèle Standard, pas de panique. Ces entités sont des outils très pratiques dans le domaine de la physique théorique.

Les fantômes de Faddeev-Popov apparaissent dans le cadre de la théorie quantique des champs de jauge. Cette théorie utilise les symétries de jauge pour décrire les forces fondamentales comme la force forte et la force faible. Cependant, lorsqu’on essaie de quantifier ces théories (c’est-à-dire de les appliquer aux niveaux les plus petits), des redondances et des incohérences apparaissent naturellement dans les calculs. C’est là que les fantômes entrent en jeu pour corriger ces problèmes.

Le terme des fantômes de Faddeev-Popov dans le Lagrangien

Les fantômes de Faddeev-Popov permettent de « fixer » la jauge, c’est-à-dire de s’assurer que les redondances mathématiques sont éliminées correctement dans les calculs. Ils ne sont pas des particules réelles mais sont introduits pour simplifier les interactions dans les théories de jauge non abéliennes (comme la force forte, qui est gouvernée par SU(3)_C).

Voici un exemple de la manière dont les fantômes de Faddeev-Popov apparaissent dans le Lagrangien du Modèle Standard :

\mathcal{L}<em>{\text{FP}} = - \bar{c}^a \left( \partial^\mu D</em>\mu^{ab} \right) c^b

Dans cette expression :

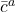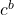  • \bar{c}^a et c^b sont les champs fantômes,
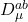  • D_\mu^{ab} est le champ covariant, qui décrit comment les fantômes interagissent avec les autres particules,
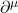  • \partial^\mu est le dérivé qui mesure les variations dans le champ.

Ce terme aide à éliminer les incohérences liées aux redondances des symétries de jauge dans les calculs, rendant ainsi les équations plus « propres » et gérables. C’est un peu comme si ces fantômes nettoyaient le désordre créé par les symétries qui se répètent inutilement.

Pourquoi avons-nous besoin des fantômes ?

Quand on travaille avec les théories de jauge, il y a souvent des termes redondants qui apparaissent dans les équations. Sans correction, ces termes pourraient rendre les calculs infinis ou incohérents. Les fantômes de Faddeev-Popov sont introduits pour neutraliser ces termes, et ils le font d’une manière très élégante.

Un autre exemple où ces fantômes sont cruciaux est la renormalisation, un processus qui permet de s’assurer que les quantités infinies apparentes dans les équations deviennent finies. Les fantômes aident à stabiliser les résultats et à rendre les calculs de théorie des champs utilisables en pratique.

Des fantômes bien spécifiques

Ce qui rend les fantômes de Faddeev-Popov uniques, c’est qu’ils sont associés spécifiquement aux théories de jauge non abéliennes. Dans les théories abéliennes comme l’électromagnétisme (gouverné par U(1)), il n’y a pas besoin de fantômes parce que les symétries de jauge ne causent pas de redondances similaires. Par contre, dans des théories comme la force forte ou la force faible, où les symétries de jauge sont plus complexes, les fantômes deviennent indispensables.

Fantômes, mais pas détectables

Comme les autres fantômes que nous avons vus, les fantômes de Faddeev-Popov ne sont pas des particules physiques. Ils n’interagissent pas avec les détecteurs dans les expériences comme celles du LHC (Large Hadron Collider). Leur rôle est strictement théorique, se limitant à s’assurer que les équations du Modèle Standard restent cohérentes et calculables.

On pourrait presque dire que les fantômes de Faddeev-Popov sont les héros méconnus de la physique des particules, faisant tout le sale boulot en coulisses pour que les calculs restent propres et utilisables. Mais, comme tous les fantômes, ils restent invisibles et n’apparaissent que dans le domaine des mathématiques.

Chapitre 7 : « La quête du boson de Higgs : Comme attraper un Pokémon rare, mais en plus subtil »

Le boson de Higgs est sans aucun doute la star du Modèle Standard. Il est souvent comparé à un « Saint Graal » pour les physiciens des particules, un peu comme un Pokémon rare que l’on cherche à capturer après des années de recherche. Ce petit bout de particule insaisissable, découvert en 2012 au CERN, est ce qui confère leur masse aux autres particules. Mais avant sa découverte, il n’était qu’une hypothèse, un fantôme parmi tant d’autres.

Le boson de Higgs est la manifestation quantique du champ de Higgs, un champ omniprésent dans l’univers. Ce champ interagit avec les particules et, grâce à ce qu’on appelle le mécanisme de Higgs, leur donne leur masse. Sans le champ de Higgs, les particules comme les bosons W et Z n’auraient pas de masse, et l’univers serait bien différent de ce qu’il est aujourd’hui.

Le terme de Higgs dans le Lagrangien

Dans le Lagrangien du Modèle Standard, le boson de Higgs est représenté par un champ scalaire \phi, et ses interactions avec les autres particules sont cruciales pour leur donner leur masse. Voici le terme qui décrit le boson de Higgs :

\mathcal{L}<em>{\text{Higgs}} = \left( D</em>{\mu} \phi \right)^\dagger \left( D^{\mu} \phi \right) - V(\phi)

Dans cette expression :

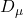  • D_{\mu} est le dérivé covariant qui décrit comment le champ de Higgs interagit avec l’espace-temps,
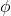  • \phi est le champ de Higgs,
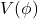  • V(\phi) est le potentiel du champ de Higgs, qui est responsable de la brisure spontanée de symétrie.

Le terme V(\phi) décrit comment le champ de Higgs acquiert une valeur non nulle dans tout l’univers, ce qui conduit à la brisure de symétrie électrofaible. C’est cette brisure qui permet aux particules de masse nulle de devenir massives.

La brisure de symétrie électrofaible

La magie du boson de Higgs réside dans la brisure spontanée de symétrie. À haute énergie, les forces électromagnétique et faible étaient unifiées en une seule force appelée la force électrofaible. Mais à basse énergie (l’énergie à laquelle nous vivons dans l’univers actuel), cette symétrie est brisée, et les bosons W et Z, qui étaient sans masse, deviennent massifs.

Le champ de Higgs joue un rôle clé dans cette transition. Imagine le champ de Higgs comme un vaste champ invisible que les particules traversent. Certaines particules interagissent fortement avec ce champ et acquièrent une masse importante (comme les bosons W et Z), tandis que d’autres, comme le photon, n’interagissent pas du tout et restent sans masse. C’est un peu comme marcher dans de la mélasse : certaines particules ont du mal à avancer et deviennent lourdes, tandis que d’autres glissent sans effort.

Une quête longue et difficile

Avant 2012, le boson de Higgs était l’un des grands mystères du Modèle Standard. Les théoriciens savaient qu’il devait exister pour que la théorie tienne debout, mais personne ne l’avait encore vu. Le CERN a lancé le Large Hadron Collider (LHC) dans le but, entre autres, de détecter ce boson insaisissable.

Après des années de recherche et de collisions de particules à haute énergie, les physiciens ont finalement détecté le boson de Higgs en 2012. Cette découverte a confirmé le Modèle Standard et a valu à François Englert et Peter Higgs le Prix Nobel de physique en 2013. C’était un peu comme attraper ce Pokémon rare après avoir exploré chaque recoin d’une carte pendant des années !

Et maintenant ?

La découverte du boson de Higgs a été un moment révolutionnaire en physique des particules, mais elle ne résout pas tout. Le boson de Higgs explique pourquoi les particules ont une masse, mais il n’explique pas tout ce que nous voulons savoir. Par exemple, il ne dit rien sur la matière noire, cette mystérieuse substance qui compose environ 27 % de l’univers, ni sur l’énergie sombre, qui semble accélérer l’expansion de l’univers.

Ainsi, bien que la quête du boson de Higgs soit terminée, la quête de la compréhension ultime de l’univers est loin d’être achevée. Il reste encore beaucoup de mystères à résoudre, et qui sait, peut-être qu’un autre boson, encore plus insaisissable, nous attend quelque part.

Chapitre 8 : « Modèle Standard vs. Réalité : Ce qu’il reste à découvrir (Spoiler : beaucoup) »

Le Modèle Standard est souvent appelé la « théorie de presque tout » en physique des particules, et à juste titre. Il a réussi à prédire l’existence de nombreuses particules avant même qu’elles ne soient découvertes, et il décrit avec une précision impressionnante trois des quatre forces fondamentales : la force électromagnétique, la force faible et la force forte. Mais, malgré tout cela, il y a des lacunes importantes dans notre compréhension de l’univers.

Les mystères non résolus

Par exemple, le Modèle Standard n’inclut pas la gravité. La force qui fait tomber une pomme ou maintient la Lune en orbite autour de la Terre ne fait tout simplement pas partie du Modèle Standard. La théorie quantique des champs, sur laquelle repose le Modèle Standard, ne réussit pas à intégrer la gravité, ce qui laisse un grand vide dans notre compréhension des interactions fondamentales.

Et puis, il y a la matière noire. Nous savons aujourd’hui que la matière ordinaire, celle qui compose tout ce que nous voyons autour de nous, ne représente qu’une petite fraction de l’univers. La majorité de la masse de l’univers est constituée de quelque chose que nous ne pouvons pas voir ni détecter directement : la matière noire. Le Modèle Standard n’offre aucune explication à ce sujet.

Il en va de même pour l’énergie sombre, cette force mystérieuse qui semble accélérer l’expansion de l’univers. Découverte récemment, l’énergie sombre défie notre compréhension actuelle de la cosmologie et des lois de la physique. Encore une fois, le Modèle Standard ne propose aucune solution.

La masse des neutrinos

Nous avons également mentionné un autre mystère dans les chapitres précédents : la masse des neutrinos. Le Modèle Standard prédit que les neutrinos sont sans masse, mais les expériences montrent qu’ils ont bel et bien une petite masse. Cela signifie que quelque chose manque ou qu’il existe une extension du Modèle Standard que nous n’avons pas encore découverte.

Le futur au-delà du Modèle Standard

Le fait que le Modèle Standard ne réponde pas à toutes les questions est à la fois frustrant et excitant. Il nous rappelle que, bien qu’il soit une théorie puissante, il n’est pas l’ultime vérité. Les physiciens cherchent aujourd’hui des théories qui vont au-delà du Modèle Standard. L’une des candidates les plus populaires est la supersymétrie, une théorie qui propose l’existence de « partenaires » supersymétriques pour chaque particule du Modèle Standard.

Une autre possibilité est la théorie des cordes, qui tente de concilier la mécanique quantique et la relativité générale pour inclure la gravité dans le cadre quantique. Selon cette théorie, les particules élémentaires ne sont pas des points, mais des petites « cordes » vibrantes. Cependant, ces théories sont encore largement hypothétiques et attendent d’être confirmées expérimentalement.

Pourquoi c’est fascinant

Le fait que nous ne connaissions pas encore toutes les réponses rend la physique des particules incroyablement excitante. Chaque nouvelle découverte pourrait bouleverser notre compréhension actuelle de l’univers. Ce que nous savons aujourd’hui pourrait être vu comme une simple approximation d’une théorie encore plus élégante et complète.

Le Modèle Standard, malgré ses lacunes, reste une réalisation incroyable. Il a survécu à des décennies de tests expérimentaux rigoureux, et la découverte du boson de Higgs en 2012 n’a fait que renforcer sa validité. Mais la quête pour comprendre l’univers dans sa totalité est loin d’être terminée.

Alors, la prochaine fois que tu entends parler de la matière noire, de l’énergie sombre ou de la masse des neutrinos, souviens-toi que nous sommes peut-être à l’aube de découvrir de nouveaux chapitres dans l’histoire de la physique. Et qui sait, peut-être que dans un futur proche, nous ajouterons un nouvel « étage » au Modèle Standard !

Check Also

Le Plan du Gouvernement Néerlandais pour Réduire les Émissions de Gaz à Effet de Serre de 50 % d’ici 2030

Introduction Bienvenue dans le monde des politiques climatiques ambitieuses! Aujourd’hui, nous nous tournons vers les …

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *

© EYELO 2024, tout droit réservé