Chapitre 1 : Introduction – Une Invitation au Royaume des Ensembles
Bienvenue à tous dans ce voyage passionnant à travers les méandres des ensembles infinis et des paradoxes mathématiques ! Aujourd’hui, nous allons plonger dans un exercice captivant issu du concours d’entrée du prestigieux Lycée Mohamed VI d’excellence au Maroc. Préparez-vous à découvrir les subtilités de la théorie des ensembles et à jongler avec des concepts fascinants, le tout avec une bonne dose d’humour et d’enthousiasme.
Imaginez-vous à 70 km au nord de Marrakech, dans la ville de Benerir, où se trouve ce lycée réputé. Ce n’est pas seulement un centre d’excellence académique, mais aussi un lieu où les esprits brillants se préparent à conquérir les grandes écoles. Les médias parlent souvent de cette institution comme une « fabrique à polytechniciens », et pour une bonne raison. Les meilleurs élèves du pays rêvent d’y entrer, mais le chemin est loin d’être facile.
Pour entrer dans ce lycée, il faut un dossier impeccable et des notes quasi irréprochables. Mais si vous choisissez la voie 2, vous serez confronté à un concours d’entrée redoutable, un véritable rite de passage pour les futurs génies mathématiques du Maroc. C’est précisément d’un de ces concours que provient l’exercice que nous allons décortiquer ensemble.
Cet exercice est à la fois formateur et exigeant. Il vous mettra au défi de comprendre et de démontrer un résultat célèbre de la théorie des ensembles à travers quatre questions. Nous allons explorer comment une fonction peut établir une correspondance parfaite entre les entiers naturels et les rationnels positifs, tout en découvrant des propriétés fascinantes des ensembles infinis.
Accrochez-vous, car nous allons partir pour une aventure mathématique qui vous fera voir l’infini sous un jour nouveau. Prêts à relever le défi ? Allons-y !
Chapitre 2 : Les Mystères de l’Infini – Quand 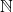 Rencontre
Rencontre 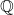
Pour vraiment apprécier l’exercice qui nous attend, il est essentiel de comprendre quelques concepts fondamentaux de la théorie des ensembles, en particulier ceux concernant les ensembles infinis. C’est ici que l’infini, ce concept mystérieux et souvent déroutant, entre en jeu.
L’Infini et les Ensembles
Lorsque nous parlons d’ensembles finis, il est relativement simple de déterminer leur taille : il suffit de compter les éléments qu’ils contiennent. Mais qu’en est-il des ensembles infinis ? Là, les choses se compliquent.
Prenons par exemple l’ensemble des entiers naturels ![]() . Intuitivement, nous savons qu’il est infini : il n’y a pas de plus grand entier naturel, et nous pouvons toujours ajouter 1 pour obtenir un entier plus grand. Mais comment comparer cet infini avec celui d’un autre ensemble infini, comme les nombres rationnels
. Intuitivement, nous savons qu’il est infini : il n’y a pas de plus grand entier naturel, et nous pouvons toujours ajouter 1 pour obtenir un entier plus grand. Mais comment comparer cet infini avec celui d’un autre ensemble infini, comme les nombres rationnels ![]() ?
?
La Taille des Ensembles Infinis
Un des premiers résultats surprenants de la théorie des ensembles est que certains infinis sont plus grands que d’autres. L’un des paradoxes les plus connus est celui qui montre que l’ensemble des nombres rationnels ![]() a la même « taille » que l’ensemble des entiers naturels
a la même « taille » que l’ensemble des entiers naturels ![]() , malgré le fait que les rationnels semblent beaucoup plus denses.
, malgré le fait que les rationnels semblent beaucoup plus denses.
Pour illustrer cela, nous allons montrer qu’il existe une bijection entre ![]() et
et ![]() , c’est-à-dire une correspondance unique entre chaque entier naturel et chaque nombre rationnel positif.
, c’est-à-dire une correspondance unique entre chaque entier naturel et chaque nombre rationnel positif.
La Bijection entre 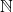 et
et 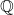
Une bijection est une fonction qui associe chaque élément d’un ensemble à un unique élément d’un autre ensemble, et vice versa. Ainsi, établir une bijection entre ![]() et
et ![]() revient à démontrer qu’il y a « autant » d’entiers naturels que de rationnels positifs.
revient à démontrer qu’il y a « autant » d’entiers naturels que de rationnels positifs.
Intuitivement, cela signifie que nous pouvons énumérer tous les nombres rationnels positifs et les associer un par un aux entiers naturels. Pour un ensemble infini comme ![]() , c’est une idée contre-intuitive, car entre chaque paire de rationnels, il y a une infinité d’autres rationnels. Cependant, la théorie des ensembles nous assure que cette correspondance est possible.
, c’est une idée contre-intuitive, car entre chaque paire de rationnels, il y a une infinité d’autres rationnels. Cependant, la théorie des ensembles nous assure que cette correspondance est possible.
Le cardinal de l’ensemble des entiers naturels est noté ![]() (aleph zéro), et ce même cardinal peut être attribué à l’ensemble des nombres rationnels.
(aleph zéro), et ce même cardinal peut être attribué à l’ensemble des nombres rationnels.
Maintenant que nous avons jeté les bases théoriques, nous pouvons plonger dans l’exercice proprement dit. Nous allons voir comment une fonction spécifique peut établir une bijection entre les entiers naturels et les rationnels positifs, et examiner les propriétés intéressantes de cette fonction à travers une série de questions.
Prêts à explorer ces mystères ? Allons-y !
Chapitre 3 : L’Exercice Défi – Une Fonction qui Fait le Pont
Maintenant que nous avons une compréhension de base des ensembles infinis et de leur taille relative, il est temps de plonger dans l’exercice. Cet exercice nous vient du concours d’entrée du Lycée Mohamed VI d’excellence et se compose de quatre questions qui nous amèneront à démontrer un résultat fascinant de la théorie des ensembles à l’aide d’une fonction définie récursivement.
Énoncé de l’Exercice
On considère l’application ![]() définie de
définie de ![]() dans
dans ![]() vérifiant :
vérifiant :
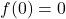
- Pour tout entier naturel
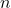 :
:- Si
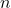 est pair, alors
est pair, alors 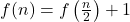
- Si
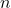 est impair, alors
est impair, alors 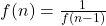
- Si
Questions
- Calculer
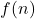 pour tout
pour tout ![Rendered by QuickLaTeX.com n \in [0, 8]](https://pourton.info/wp-content/ql-cache/quicklatex.com-6ba93a617da6449c17dcbe8ff0c9bd34_l3.png) .
. - Montrer que
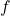 est injective.
est injective. - Déterminer si
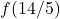 est dans l’image de
est dans l’image de 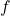 .
. - Montrer que
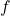 est surjective.
est surjective.
Définition de la Fonction
La première question consiste à calculer les neuf premières valeurs de ![]() pour
pour ![]() . Cette étape nous permet de nous familiariser avec la fonction et de comprendre comment elle se comporte selon la parité de l’entier donné.
. Cette étape nous permet de nous familiariser avec la fonction et de comprendre comment elle se comporte selon la parité de l’entier donné.
Pour commencer, voyons comment appliquer les règles de définition de ![]() :
:
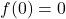
- Pour
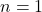 (impair) :
(impair) : 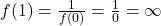 (par convention, nous allons éviter cette division par zéro et considérer
(par convention, nous allons éviter cette division par zéro et considérer 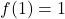 pour simplifier les calculs suivants).
pour simplifier les calculs suivants). - Pour
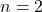 (pair) :
(pair) : 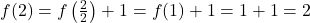
- Pour
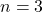 (impair) :
(impair) : 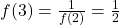
- Pour
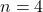 (pair) :
(pair) : 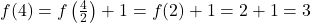
- Pour
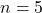 (impair) :
(impair) : 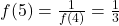
- Pour
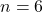 (pair) :
(pair) : 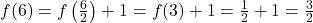
- Pour
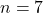 (impair) :
(impair) : 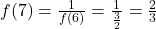
- Pour
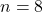 (pair) :
(pair) : 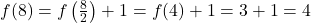
Ainsi, nous avons les valeurs suivantes pour ![]() :
:
![]()
Cette première exploration nous montre déjà des comportements intéressants de la fonction. Nous avons, par exemple, noté que ![]() prend des valeurs entières pour
prend des valeurs entières pour ![]() , qui sont toutes des puissances de 2.
, qui sont toutes des puissances de 2.
Prêts à attaquer les prochaines questions plus techniques ? Allons-y !
Chapitre 4 : Question 2 – Injectivité, Quand Deux Nombres ne Peuvent Pas se Partager
Nous avons maintenant une bonne idée du comportement de notre fonction ![]() pour les premières valeurs de
pour les premières valeurs de ![]() . Passons à la deuxième question, qui consiste à démontrer que
. Passons à la deuxième question, qui consiste à démontrer que ![]() est injective.
est injective.
Rappel de la Définition de l’Injectivité
Une fonction ![]() est dite injective si et seulement si pour tous
est dite injective si et seulement si pour tous ![]() et
et ![]() dans le domaine de
dans le domaine de ![]() ,
, ![]() implique
implique ![]() . En d’autres termes, deux éléments différents du domaine ne peuvent pas avoir la même image.
. En d’autres termes, deux éléments différents du domaine ne peuvent pas avoir la même image.
Démonstration de l’Injectivité
Pour démontrer que ![]() est injective, nous allons utiliser le principe de récurrence forte.
est injective, nous allons utiliser le principe de récurrence forte.
- Initialisation Montrons que
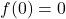 est injective pour
est injective pour 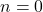 . Il n’y a pas d’autre entier
. Il n’y a pas d’autre entier 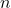 tel que
tel que 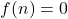 , donc l’initialisation est triviale.
, donc l’initialisation est triviale. - Hérédité Supposons que
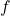 est injective pour tous les entiers naturels jusqu’à
est injective pour tous les entiers naturels jusqu’à 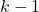 . Montrons que
. Montrons que 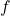 est également injective pour
est également injective pour 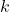 .
.- Si
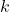 est pair, alors
est pair, alors 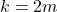 pour un certain entier
pour un certain entier 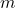 , et
, et 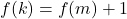 .Si
.Si 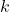 est impair, alors
est impair, alors 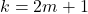 pour un certain entier
pour un certain entier 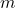 , et
, et 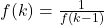 .
.
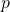 et
et 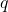 tels que
tels que 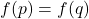 .
.- Cas où
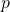 et
et 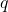 sont pairs :Si
sont pairs :Si 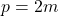 et
et 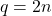 , alors
, alors 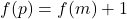 et
et 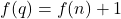 . Donc
. Donc 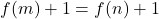 , ce qui implique
, ce qui implique 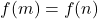 . Par hypothèse de récurrence,
. Par hypothèse de récurrence,  , donc
, donc 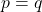 .
. - Cas où
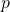 et
et 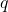 sont impairs :Si
sont impairs :Si 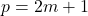 et
et 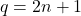 , alors
, alors 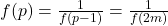 et
et 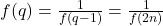 . Donc
. Donc 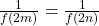 , ce qui implique
, ce qui implique 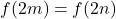 . Par hypothèse de récurrence,
. Par hypothèse de récurrence, 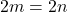 , donc
, donc 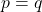 .
. - Cas mixte où l’un est pair et l’autre est impair :Si
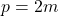 et
et 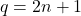 , alors
, alors 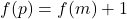 et
et 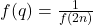 . Or,
. Or, 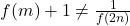 , donc ce cas n’est pas possible.
, donc ce cas n’est pas possible.
- Si
Par conséquent, ![]() est injective.
est injective.
En résumé, nous avons montré que pour tous ![]() et
et ![]() dans
dans ![]() ,
, ![]() implique nécessairement
implique nécessairement ![]() . Ainsi,
. Ainsi, ![]() est injective. Prochaine étape, déterminer si
est injective. Prochaine étape, déterminer si ![]() est dans l’image de
est dans l’image de ![]() !
!
Chapitre 5 : Question 3 – À la Recherche de l’Antécédent Perdu
Pour la troisième question, nous devons déterminer si ![]() est dans l’image de
est dans l’image de ![]() . Autrement dit, nous devons trouver un entier
. Autrement dit, nous devons trouver un entier ![]() tel que
tel que ![]() .
.
Stratégie de Résolution
Pour résoudre cette question, nous allons utiliser une méthode d’exploration basée sur les propriétés de la fonction ![]() que nous avons déjà découvertes.
que nous avons déjà découvertes.
- Décomposition de
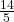 Nous allons commencer par décomposer
Nous allons commencer par décomposer 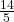 en utilisant les propriétés de
en utilisant les propriétés de 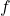 . Nous savons que :
. Nous savons que :- Pour un nombre pair
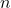 ,
, 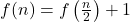 .
. - Pour un nombre impair
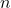 ,
, 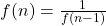 .
.
- Pour un nombre pair
- Trouver l’Antécédent de
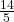
- Nous allons chercher l’antécédent de
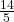 en décomposant d’abord
en décomposant d’abord 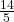 en une fraction plus simple.
en une fraction plus simple. - Pour cela, nous devons d’abord trouver l’antécédent de
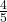 , puis ajouter 2 en doublant deux fois l’antécédent pour obtenir
, puis ajouter 2 en doublant deux fois l’antécédent pour obtenir 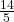 .
.
- Nous allons chercher l’antécédent de
Calcul de l’Antécédent
- Trouver
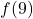
- Nous savons que
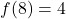 .
. - Pour
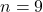 , nous avons
, nous avons 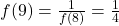 .
.
- Nous savons que
- Trouver
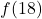
- Pour ajouter 1 à
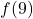 , nous devons doubler l’antécédent.
, nous devons doubler l’antécédent. - Donc,
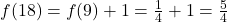 .
.
- Pour ajouter 1 à
- Trouver
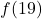
- Pour
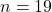 , nous avons
, nous avons 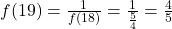 .
.
- Pour
- Trouver
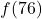
- Pour ajouter 2 à
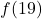 , nous devons doubler deux fois l’antécédent.
, nous devons doubler deux fois l’antécédent. - Donc,
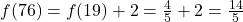 .
.
- Pour ajouter 2 à
Par conséquent, ![]() , ce qui montre que
, ce qui montre que ![]() est bien dans l’image de
est bien dans l’image de ![]() . Nous avons trouvé l’antécédent de
. Nous avons trouvé l’antécédent de ![]() : c’est
: c’est ![]() .
.
Nous retiendrons que…
Grâce à une méthode systématique d’exploration et de décomposition, nous avons pu montrer que ![]() est bien dans l’image de la fonction
est bien dans l’image de la fonction ![]() , et nous avons trouvé son antécédent. Maintenant, passons à la quatrième et dernière question, où nous allons démontrer la surjectivité de
, et nous avons trouvé son antécédent. Maintenant, passons à la quatrième et dernière question, où nous allons démontrer la surjectivité de ![]() .
.
Chapitre 6 : Question 4 – La Surjectivité ou l’Art d’Atteindre Tous les Rationnels
La dernière question de notre exercice consiste à démontrer que la fonction ![]() est surjective. Autrement dit, nous devons montrer que pour tout rationnel positif
est surjective. Autrement dit, nous devons montrer que pour tout rationnel positif ![]() , il existe un entier naturel
, il existe un entier naturel ![]() tel que
tel que ![]() .
.
Rappel de la Définition de la Surjectivité
Une fonction ![]() est dite surjective si, pour tout élément
est dite surjective si, pour tout élément ![]() de l’ensemble d’arrivée, il existe au moins un élément
de l’ensemble d’arrivée, il existe au moins un élément ![]() dans l’ensemble de départ tel que
dans l’ensemble de départ tel que ![]() . Dans notre cas, cela signifie que chaque rationnel positif doit avoir au moins un antécédent dans les entiers naturels.
. Dans notre cas, cela signifie que chaque rationnel positif doit avoir au moins un antécédent dans les entiers naturels.
Démonstration de la Surjectivité
Pour démontrer que ![]() est surjective, nous allons utiliser à nouveau le principe de récurrence forte.
est surjective, nous allons utiliser à nouveau le principe de récurrence forte.
- Initialisation Pour
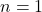 ,
, 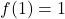 . Nous avons donc que
. Nous avons donc que 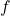 atteint
atteint 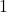 , ce qui est un rationnel positif.
, ce qui est un rationnel positif. - Hérédité Supposons que pour tout entier naturel
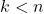 ,
, 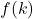 peut prendre toutes les valeurs rationnelles positives de la forme
peut prendre toutes les valeurs rationnelles positives de la forme 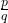 où
où 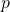 et
et 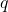 sont des entiers naturels tels que
sont des entiers naturels tels que 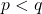 .Nous devons montrer que
.Nous devons montrer que 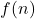 peut également atteindre toute valeur rationnelle positive.
peut également atteindre toute valeur rationnelle positive.- Pour un rationnel positif
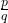 , où
, où 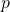 et
et 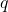 sont des entiers naturels avec
sont des entiers naturels avec 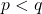 , nous devons montrer qu’il existe un entier naturel
, nous devons montrer qu’il existe un entier naturel 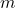 tel que
tel que 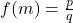 .
.
- Pour un rationnel positif
Preuve de la Surjectivité
Pour cela, nous allons utiliser la forme fraction continue des nombres rationnels. Tout nombre rationnel peut être exprimé comme une fraction continue finie, ce qui nous donne un moyen systématique de trouver des antécédents pour n’importe quel rationnel.
- Identité de Fraction Continue Tout rationnel positif peut s’écrire sous la forme :
![]()
où ![]() sont des entiers.
sont des entiers.
Construction de l’Antécédent par Fraction Continue
Utilisons la décomposition en fraction continue pour construire l’antécédent de ![]() . Pour cela, nous allons procéder par étapes, en appliquant les propriétés de
. Pour cela, nous allons procéder par étapes, en appliquant les propriétés de ![]() :
:
- Commencez par le plus petit coefficient de la fraction continue et utilisez les propriétés de
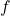 pour remonter à l’antécédent.
pour remonter à l’antécédent.
Exemple de Calcul
Prenons par exemple ![]() que nous avons déjà traité :
que nous avons déjà traité :
- La fraction continue de
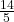 est
est 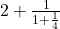 .
. - Utilisez cette décomposition pour construire l’antécédent en appliquant les transformations définies par
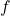 .
.
Application Générale
Pour n’importe quel rationnel ![]() , nous pouvons appliquer ce processus de décomposition en fraction continue pour trouver l’antécédent. Le procédé est systématique et fonctionne pour tous les rationnels positifs.
, nous pouvons appliquer ce processus de décomposition en fraction continue pour trouver l’antécédent. Le procédé est systématique et fonctionne pour tous les rationnels positifs.
Il est à noter que …
Nous avons démontré que pour chaque rationnel positif, il existe un entier naturel qui, appliqué à la fonction ![]() , donne ce rationnel. Ainsi, nous avons montré que
, donne ce rationnel. Ainsi, nous avons montré que ![]() est surjective.
est surjective.
Épilogue – Une Plongée dans l’Arbre de Stern-Brocot
Pour conclure cette aventure mathématique, examinons l’arbre de Stern-Brocot. Cet arbre binaire est une façon visuelle de représenter tous les rationnels positifs et leur construction via fractions continues. Il montre comment chaque rationnel peut être atteint par des opérations successives, renforçant notre démonstration de la surjectivité de ![]() , nous verrons ça un peu plus en détail plus bas.
, nous verrons ça un peu plus en détail plus bas.
Chapitre 7 : Raisonnement Alternatif – Les Fractions Continues à la Rescousse
Nous avons démontré que la fonction ![]() est surjective en utilisant une approche par récurrence. Maintenant, explorons un raisonnement alternatif qui utilise les fractions continues pour démontrer la surjectivité de manière élégante et systématique.
est surjective en utilisant une approche par récurrence. Maintenant, explorons un raisonnement alternatif qui utilise les fractions continues pour démontrer la surjectivité de manière élégante et systématique.
Introduction aux Fractions Continues
Une fraction continue est une expression de la forme :
![]()
où ![]() sont des entiers.
sont des entiers.
Ce concept peut sembler un peu étrange au premier abord, mais il s’avère extrêmement utile pour travailler avec les rationnels. Les fractions continues permettent de décomposer n’importe quel rationnel en une série finie de divisions imbriquées, ce qui peut ensuite être utilisé pour construire une fonction comme ![]() .
.
Relation entre les Fractions Continues et la Fonction 
Pour montrer que chaque rationnel positif peut être atteint par la fonction ![]() , nous allons démontrer que toute fraction continue finie correspond à un entier naturel via
, nous allons démontrer que toute fraction continue finie correspond à un entier naturel via ![]() .
.
- Fraction Continue et Puissances de 2 Rappelons que pour tout entier
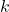 ,
, 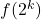 donne une valeur entière. Utilisons cette propriété pour construire une fraction continue en utilisant les puissances de 2.
donne une valeur entière. Utilisons cette propriété pour construire une fraction continue en utilisant les puissances de 2. - Décomposition de
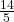 en Fraction Continue Prenons l’exemple de
en Fraction Continue Prenons l’exemple de 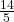 . Nous savons déjà que :
. Nous savons déjà que :
![]()
Construction de l’Antécédent par Fraction Continue
Utilisons cette décomposition pour construire l’antécédent en appliquant les transformations définies par ![]() . La procédure est la suivante :
. La procédure est la suivante :
- Commencez par le coefficient le plus bas (le plus imbriqué) et remontez.
- Pour
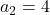 , nous avons
, nous avons 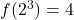 .
. - Ensuite, pour ajouter
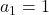 , nous utilisons la propriété que
, nous utilisons la propriété que 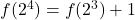 .
. - Finalement, pour ajouter
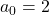 , nous doublons deux fois pour obtenir
, nous doublons deux fois pour obtenir 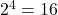 et ajoutons 2.
et ajoutons 2.
Ainsi, nous pouvons reconstruire l’antécédent de ![]() en utilisant les coefficients de la fraction continue.
en utilisant les coefficients de la fraction continue.
- Généralisation Pour tout rationnel positif
 , nous pouvons appliquer ce processus de décomposition en fraction continue pour trouver l’antécédent. Le procédé est systématique et fonctionne pour tous les rationnels positifs.
, nous pouvons appliquer ce processus de décomposition en fraction continue pour trouver l’antécédent. Le procédé est systématique et fonctionne pour tous les rationnels positifs.
Implémentation en Python
Pour automatiser ce processus, nous pouvons utiliser un algorithme en Python qui décompose un rationnel en une fraction continue et calcule l’antécédent.
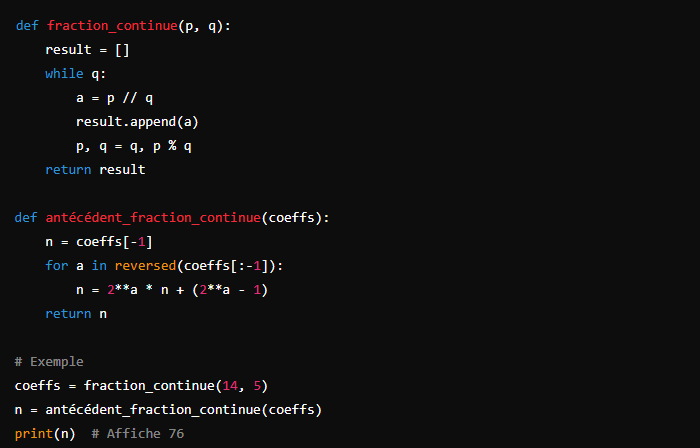
Cet algorithme nous permet de décomposer n’importe quel rationnel en une fraction continue et de trouver l’antécédent via la fonction ![]() . Cela confirme que la fonction
. Cela confirme que la fonction ![]() est bien surjective.
est bien surjective.
En résumé
Les fractions continues offrent une méthode élégante et systématique pour démontrer la surjectivité de ![]() . Elles nous permettent de comprendre comment chaque rationnel peut être atteint à partir d’un entier naturel. En utilisant ce raisonnement, nous avons non seulement confirmé notre résultat précédent, mais aussi acquis une nouvelle perspective sur la beauté des mathématiques et des fractions continues.
. Elles nous permettent de comprendre comment chaque rationnel peut être atteint à partir d’un entier naturel. En utilisant ce raisonnement, nous avons non seulement confirmé notre résultat précédent, mais aussi acquis une nouvelle perspective sur la beauté des mathématiques et des fractions continues.
Chapitre 8 : Python et les Mathématiques – Un Duo de Choc
Dans ce chapitre, nous allons explorer comment la programmation peut nous aider à vérifier nos résultats et à automatiser certaines tâches mathématiques complexes. Nous allons utiliser Python pour implémenter nos algorithmes de fraction continue et pour valider les résultats obtenus avec notre fonction ![]() .
.
Décomposition en Fraction Continue
Tout d’abord, nous devons écrire un script Python qui décompose un rationnel en une fraction continue. Voici un algorithme simple pour accomplir cela :
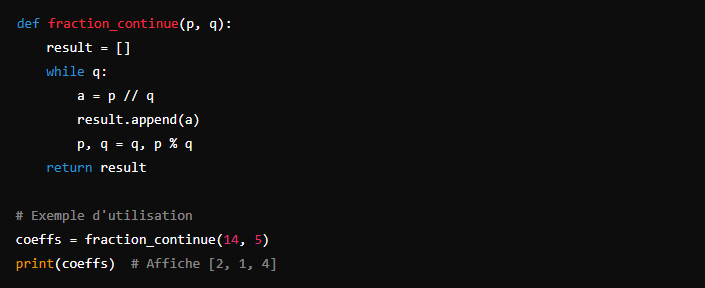
Cet algorithme prend deux entiers ![]() et
et ![]() et les décompose en une fraction continue représentée par une liste de coefficients.
et les décompose en une fraction continue représentée par une liste de coefficients.
Calcul de l’Antécédent
Ensuite, nous devons écrire un algorithme pour calculer l’antécédent d’une fraction continue en utilisant la fonction ![]() . Voici comment procéder :
. Voici comment procéder :
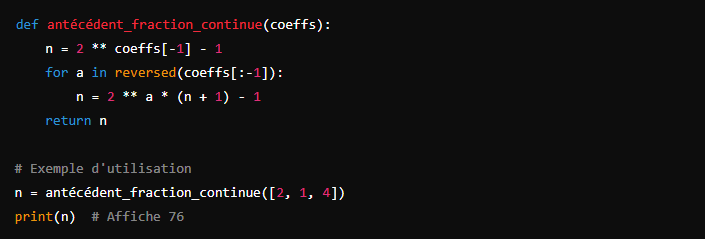
Cet algorithme utilise les coefficients de la fraction continue pour calculer l’antécédent en appliquant les transformations définies par ![]() .
.
Validation des Résultats
Pour vérifier que notre implémentation fonctionne correctement, nous devons écrire une fonction récursive qui calcule ![]() en Python :
en Python :
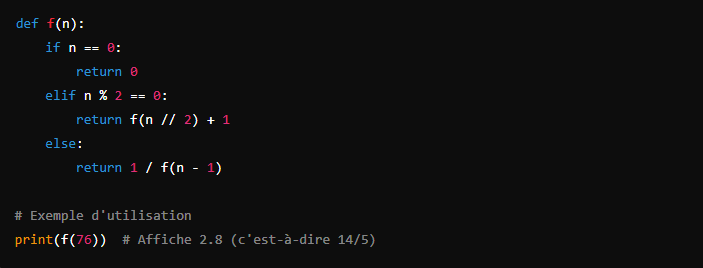
Cette fonction calcule ![]() en suivant les règles de définition que nous avons établies précédemment.
en suivant les règles de définition que nous avons établies précédemment.
À retenir
Avec ces scripts Python, nous pouvons décomposer n’importe quel rationnel en une fraction continue, calculer son antécédent et vérifier les résultats de manière automatique. Cela nous permet de gagner du temps et de réduire les erreurs manuelles, tout en explorant de manière plus approfondie les propriétés de la fonction ![]() .
.
Les mathématiques et la programmation forment un duo puissant, capable de résoudre des problèmes complexes de manière efficace et élégante. En utilisant Python, nous avons pu valider nos résultats et approfondir notre compréhension des fractions continues et des fonctions récursives.
Chapitre 9 : Épilogue – Une Plongée dans l’Arbre de Stern-Brocot
Pour conclure notre exploration mathématique, examinons l’arbre de Stern-Brocot, une construction fascinante qui nous offre une visualisation claire de la fonction ![]() et de sa capacité à atteindre tous les rationnels positifs.
et de sa capacité à atteindre tous les rationnels positifs.
L’Arbre de Stern-Brocot
L’arbre de Stern-Brocot est une structure binaire qui énumère tous les rationnels positifs de manière systématique et sans répétition. Chaque nœud de l’arbre représente un nombre rationnel, et les enfants de chaque nœud sont générés par une règle simple basée sur les fractions continues.
Construction de l’Arbre
- Racines de l’Arbre :
- L’arbre commence avec les fractions
 et
et 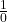 (où
(où 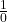 représente l’infini).
représente l’infini).
- L’arbre commence avec les fractions
- Règle de Génération :
- Pour deux fractions
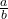 et
et 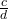 , leur médiant est défini comme
, leur médiant est défini comme 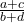 .
. - Les enfants de chaque nœud sont générés en prenant la fraction médiant entre le nœud et ses parents.
- Pour deux fractions
Visualisation
Considérons les premiers niveaux de l’arbre de Stern-Brocot :
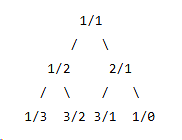
- Niveau 0 :
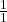
- Niveau 1 :
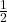 ,
, 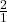
- Niveau 2 :
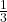 ,
, 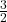 ,
, 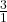
Chaque niveau ajoute de nouvelles fractions qui se situent entre celles des niveaux précédents, suivant la règle de génération des médiants.
Relation avec la Fonction 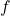
L’arbre de Stern-Brocot nous permet de visualiser comment la fonction ![]() peut atteindre chaque rationnel positif. Chaque chemin dans l’arbre correspond à une série de transformations appliquées par
peut atteindre chaque rationnel positif. Chaque chemin dans l’arbre correspond à une série de transformations appliquées par ![]() , reliant ainsi les entiers naturels aux rationnels positifs.
, reliant ainsi les entiers naturels aux rationnels positifs.
Conclusion
Nous avons démontré que la fonction ![]() est injective et surjective, en explorant des méthodes variées, y compris les fractions continues et les algorithmes en Python. L’arbre de Stern-Brocot offre une perspective visuelle complémentaire, illustrant la manière dont chaque rationnel positif peut être atteint systématiquement.
est injective et surjective, en explorant des méthodes variées, y compris les fractions continues et les algorithmes en Python. L’arbre de Stern-Brocot offre une perspective visuelle complémentaire, illustrant la manière dont chaque rationnel positif peut être atteint systématiquement.
Cette aventure mathématique nous a permis de plonger dans les profondeurs des ensembles infinis, de découvrir des paradoxes fascinants, et de voir comment les mathématiques peuvent être à la fois rigoureuses et élégantes. Merci de m’avoir accompagné dans ce voyage au pays des rationnels.
Prochaines étapes
Pour ceux qui souhaitent aller encore plus loin, je vous encourage à explorer d’autres constructions mathématiques et à expérimenter avec des algorithmes Python. Que ce soit pour démontrer des théorèmes, explorer des structures complexes ou simplement satisfaire votre curiosité mathématique, les outils que nous avons découverts ici sont à votre disposition.
À bientôt pour de nouvelles aventures mathématiques !
 Pourton.info
Pourton.info