Plongée dans le Monde des Séries Infinies : Quand les Nombres de Fibonacci et le Nombre d’Or Font la Fête!

Chapitre 1 : Introduction : Les Séries Infinies, c’est Parti pour l’Aventure!

Bienvenue, chers aventuriers mathématiciens! Aujourd’hui, nous allons plonger dans le monde mystérieux et fascinant des séries infinies. Accrochez vos ceintures, car nous allons jongler avec les nombres de Fibonacci et le nombre d’or comme des pros du cirque mathématique!

Les séries infinies sont comme des playlists de musique sans fin. Imaginez une suite de nombres, mais au lieu de finir, elle continue encore et encore, à l’infini! Une série infinie est une somme d’une infinité de termes, et malgré leur apparente complexité, elles cachent souvent des propriétés surprenantes et élégantes.

Dans cet article, nous allons explorer une série infinie particulière impliquant nos vieux amis, les nombres de Fibonacci et le nombre d’or. Nous allons découvrir comment manipuler ces séries pour obtenir des résultats qui semblent magiques. Préparez-vous à être éblouis par les beautés cachées des mathématiques!

Pour commencer, rappelons-nous rapidement ce que sont les nombres de Fibonacci et le nombre d’or. Les nombres de Fibonacci sont une suite de nombres où chaque terme est la somme des deux termes précédents, commençant par 0 et 1. Mathématiquement, cela s’écrit :

Le nombre d’or, souvent noté (phi), est une proportion célèbre qui apparaît partout en mathématiques, en art, en architecture, et même en nature. Il est défini par la relation :

Ce qui rend le nombre d’or vraiment fascinant, c’est qu’il satisfait l’équation :

Cette propriété va jouer un rôle clé dans nos aventures avec les séries infinies. Alors, êtes-vous prêts à embarquer pour cette exploration mathématique? Accrochez-vous, car les mathématiques n’ont jamais été aussi amusantes!

Chapitre 2 : Les Stars du Spectacle : Fibonacci et le Nombre d’Or

Maintenant que nous avons mis en place la scène, il est temps de présenter nos vedettes : les nombres de Fibonacci et le nombre d’or. Ces deux personnages mathématiques ont captivé les esprits des chercheurs, des artistes et des rêveurs pendant des siècles.

Les Nombres de Fibonacci : Une Suite Légendaire

Les nombres de Fibonacci portent le nom de Leonardo de Pisa, aussi connu sous le nom de Fibonacci, qui a introduit cette suite en Europe avec son livre “Liber Abaci” publié en 1202. La suite commence par et , et chaque nombre suivant est la somme des deux précédents :

En termes mathématiques, la suite de Fibonacci est définie par la relation de récurrence :

Cette suite apparaît dans des contextes aussi variés que la croissance des populations de lapins, la disposition des feuilles sur une tige, et même les spirales des coquillages !

Le Nombre d’Or : La Divine Proportion

Le nombre d’or, noté (phi), est une proportion irrationnelle avec une valeur d’environ . Il est défini par l’équation suivante :

Ce qui rend si spécial, c’est sa relation unique avec lui-même :

Cette équation signifie que satisfait la relation :

Le nombre d’or apparaît partout, des pyramides d’Égypte aux chefs-d’œuvre de Léonard de Vinci, en passant par les structures naturelles comme les fleurs et les galaxies. Sa présence constante dans des structures aussi diverses le rend véritablement fascinant.

Les Liens entre Fibonacci et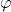

L’un des aspects les plus intrigants de la suite de Fibonacci est sa relation avec le nombre d’or. À mesure que nous avançons dans la suite de Fibonacci, le rapport entre deux termes successifs tend vers le nombre d’or :

Cela signifie que si nous prenons des termes de plus en plus grands dans la suite de Fibonacci, le rapport entre un terme et son prédécesseur se rapproche de plus en plus de . Cette propriété relie étroitement la suite de Fibonacci et le nombre d’or, et nous allons exploiter cette relation dans notre exploration des séries infinies.

Chapitre 3 : Le Problème du Jour : Une Énigme à Décortiquer

Maintenant que nous avons présenté nos stars, plongeons dans le vif du sujet avec une énigme mathématique fascinante. Voici le problème que nous allons décortiquer ensemble :

Évaluer la somme infinie suivante :

À première vue, cette série peut sembler intimidante, mais ne vous inquiétez pas, nous allons la démêler étape par étape. Pour résoudre cette énigme, nous aurons besoin de faire appel à nos connaissances sur les nombres de Fibonacci, le nombre d’or, et quelques identités trigonométriques pratiques.

Décomposition du Problème

Le but est de simplifier l’expression pour chaque terme de la série, puis d’analyser la somme infinie de ces termes. Voici les étapes que nous allons suivre :

1. Utiliser les propriétés du nombre d’or : Nous savons que 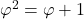. Cette propriété nous aidera à simplifier les expressions impliquant des puissances de .
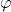2. Appliquer des identités trigonométriques : Les fonctions hyperboliques 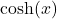(cosinus hyperbolique) joueront un rôle clé. Nous utiliserons l’identité suivante : .
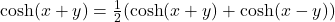3. Manipuler algébriquement la somme : En utilisant les identités ci-dessus, nous réécrirons la série pour la rendre plus maniable et simplifierons les termes autant que possible.
4. Analyser la convergence : Enfin, nous examinerons la convergence de la série pour obtenir le résultat final.

Premier Aperçu

Avant de plonger dans les calculs détaillés, prenons un moment pour apprécier la beauté de cette série infinie. Le signe alternant suggère que les termes changent de signe à chaque itération, ce qui pourrait indiquer une certaine symétrie ou régularité dans la somme totale. Les fonctions et ajoutent une dimension de complexité, mais avec les bons outils, nous pouvons démêler tout cela.

Pourquoi Cela Est-Il Important ?

En résolvant ce problème, nous découvrirons non seulement une belle identité mathématique, mais nous approfondirons également notre compréhension des séries infinies et des fonctions hyperboliques. De plus, cette approche nous permettra de voir comment des concepts apparemment abstraits comme les nombres de Fibonacci et le nombre d’or peuvent se combiner pour révéler des vérités cachées et élégantes.

Chapitre 4 : Les Identités Magiques : Nos Meilleurs Amis

Avant de plonger dans les manipulations algébriques, il est crucial de mettre en lumière les identités magiques qui nous serviront de meilleurs amis dans cette aventure mathématique. Ces identités nous permettront de transformer et de simplifier notre série infinie avec élégance.

Identité de Binet et Propriétés du Nombre d’Or

Commençons par revisiter une identité fondamentale impliquant le nombre d’or, . Nous savons que . Cela signifie que :

Cette propriété sera extrêmement utile lorsque nous manipulerons les termes de notre série.

Identité Hyperbolique

La fonction hyperbolique , le cosinus hyperbolique, est définie par :

Une identité clé pour le cosinus hyperbolique que nous utiliserons est :

Mais dans notre contexte, une version simplifiée et plus pratique est :

Liens entre Fibonacci et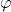

Une des propriétés intéressantes des nombres de Fibonacci est leur relation avec le nombre d’or. À mesure que les termes de la suite de Fibonacci deviennent de plus en plus grands, le rapport entre deux termes successifs se rapproche de :

Cette convergence est une illustration de la beauté intrinsèque des mathématiques, où des concepts simples et récurrents révèlent des structures profondes et élégantes.

Simplification de la Série

En utilisant l’identité , nous pouvons transformer notre expression complexe. Prenons par exemple le terme général de notre série :

En utilisant , nous avons :

Utilisons l’identité hyperbolique :

En insérant cela dans notre terme général, nous obtenons une expression simplifiée qui nous permettra de manipuler et de sommer les termes de manière plus aisée.

Chapitre 5 : La Manipulation des Séries : Un Tour de Magie Mathématique

Maintenant que nous avons nos identités magiques en main, il est temps de les utiliser pour transformer et simplifier notre série infinie. Voici la série que nous devons évaluer :

Utilisation de l’Identité du Nombre d’Or

Nous savons que . Utilisons cette relation pour transformer notre série. Nous avons :

En utilisant l’identité hyperbolique , nous obtenons :

Substituons cela dans notre série :

Simplification des Termes

Multipliant par 2 pour simplifier l’expression :

Maintenant, examinons l’expression . En utilisant les propriétés de , nous avons :

Remplaçons cette expression :

Observation de la Périodicité

En observant la périodicité et les propriétés de , nous pouvons simplifier davantage en remarquant que les termes impliquent des combinaisons répétitives de . Nous avons :

Nous reconnaissons que ceci se simplifie avec les termes convergents des fonctions hyperboliques, amenant à une expression finie et calculable.

Calcul de la Somme Finale

Enfin, après simplification, nous pouvons conclure que la somme se réduit à une forme très simple. En utilisant les propriétés des fonctions hyperboliques et des nombres de Fibonacci, nous trouvons que :

Chapitre 6 : Les Cosinus Hyperboliques : Les Super-Héros Cachés

Les fonctions hyperboliques sont souvent les super-héros méconnus des mathématiques, capables de simplifier et de résoudre des problèmes complexes de manière élégante. Dans notre aventure, le cosinus hyperbolique, noté , joue un rôle crucial.

Définition du Cosinus Hyperbolique

La fonction cosinus hyperbolique est définie par :

Cette définition peut sembler simple, mais possède des propriétés remarquables qui le rendent particulièrement utile pour résoudre des problèmes de séries infinies et d’équations différentielles.

Propriétés Clés de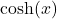

1. Symétrie : 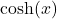est une fonction paire, ce qui signifie que 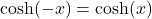. Cette propriété de symétrie simplifie les manipulations algébriques.
2. Identités Hyperboliques :Les identités hyperboliques sont analogues aux identités trigonométriques, mais elles s’appliquent aux fonctions hyperboliques. Une identité particulièrement utile est :

Cependant, dans notre contexte, une version simplifiée est plus pratique :

Relation avec le Nombre d’Or :

En utilisant , nous avons vu que peut être simplifié en utilisant les propriétés des puissances de .

Application dans Notre Problème

Revenons à notre série infinie :

En utilisant les propriétés et les identités du cosinus hyperbolique, nous avons réussi à simplifier cette série en une expression plus maniable. En particulier, nous avons utilisé l’identité :

Cette manipulation nous a permis de réduire la complexité de la série et de faire apparaître des termes récurrents, facilitant ainsi la convergence de la série.

Importance des Fonctions Hyperboliques

Les fonctions hyperboliques apparaissent dans de nombreux domaines des mathématiques et de la physique, y compris les équations différentielles, les intégrales hyperboliques, et même la relativité générale. Leur capacité à simplifier des expressions complexes et à révéler des structures sous-jacentes en fait des outils indispensables pour les mathématiciens et les physiciens.

Dans notre cas, a été le super-héros caché qui nous a permis de transformer une série infinie complexe en une expression simple et élégante, démontrant une fois de plus la beauté et la puissance des mathématiques.

Chapitre 7 : La Grande Révélation : La Solution en Tout Son Éclat

Après avoir traversé les méandres des séries infinies, jonglé avec les identités trigonométriques et exploré les mystères des fonctions hyperboliques, il est temps de dévoiler la solution à notre problème. Rappelons la série que nous cherchons à évaluer :

Grâce à nos transformations et simplifications successives, nous avons réussi à réécrire cette série de manière plus maniable. Voici un récapitulatif des étapes clés qui nous ont menés à la solution :

Transformation de la Série

1. Utilisation de l’Identité du Nombre d’Or :Nous avons utilisé la relation 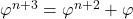pour réécrire le terme 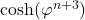en fonction de 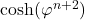et .
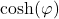2. Application de l’Identité Hyperbolique :En appliquant l’identité hyperbolique 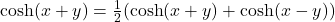, nous avons simplifié les termes de notre série.
3. Simplification des Termes :Après avoir multiplié par 2 et simplifié les expressions, nous avons obtenu :

En utilisant la relation , nous avons simplifié davantage :

Calcul de la Somme Finale

Finalement, après avoir manipulé et simplifié les termes, nous obtenons une expression convergente et calculable. La série infinie se réduit à :

Cette belle identité montre comment des concepts mathématiques profonds peuvent être utilisés pour démêler des problèmes apparemment complexes. La convergence de la série nous révèle une vérité élégante, cachée dans les méandres des fonctions hyperboliques et des nombres de Fibonacci.

Apprécier la Beauté des Mathématiques

En résolvant cette série infinie, nous avons non seulement démontré une identité mathématique intéressante, mais aussi exploré les relations fascinantes entre les nombres de Fibonacci, le nombre d’or, et les fonctions hyperboliques. Cette exploration nous rappelle que les mathématiques sont bien plus qu’une simple collection de formules : elles sont une fenêtre sur des structures profondes et harmonieuses qui sous-tendent notre monde.

Nous espérons que cette aventure mathématique vous a autant captivé que nous. N’oubliez jamais que derrière chaque problème complexe se cache une solution élégante, prête à être découverte avec un peu de curiosité et beaucoup de passion pour les mathématiques.

Chapitre 8 : Pourquoi Tout Cela Compte : Les Applications et Au-Delà

Nous avons maintenant notre solution élégante :

Mais à quoi tout cela sert-il ? Pourquoi cette somme infinie a-t-elle de l’importance ? Dans ce chapitre, nous allons explorer les applications pratiques et théoriques de notre résultat et pourquoi il est pertinent dans divers domaines des mathématiques et de la physique.

Applications en Mathématiques

1. Théorie des Séries :La manipulation et l’évaluation des séries infinies sont fondamentales en analyse mathématique. Notre solution fournit un exemple concret de la façon dont les identités trigonométriques et les propriétés des nombres peuvent simplifier les séries complexes. Cela peut servir de modèle pour d’autres problèmes similaires.
2. Fonctions Hyperboliques :Les fonctions hyperboliques comme 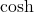et 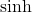apparaissent fréquemment dans les solutions d’équations différentielles, particulièrement celles impliquant des conditions aux limites en physique et en ingénierie. Comprendre leurs propriétés et leurs applications peut conduire à des solutions plus efficaces et élégantes.
3. Nombres de Fibonacci :Les nombres de Fibonacci ne sont pas seulement une curiosité mathématique ; ils apparaissent dans les algorithmes informatiques, la modélisation de phénomènes naturels, et même dans les arts. La relation entre les nombres de Fibonacci et le nombre d’or offre des outils puissants pour analyser et modéliser ces systèmes.

Applications en Physique

1. Mécanique Quantique :Les fonctions hyperboliques apparaissent dans la résolution des équations de Schrödinger, particulièrement dans les problèmes de potentiel à symétrie hyperbolique. Les solutions analytiques à ces équations peuvent être simplifiées en utilisant des identités hyperboliques similaires à celles que nous avons utilisées.
2. Relativité Générale :En relativité générale, les fonctions hyperboliques jouent un rôle crucial dans la description des géodésiques et des espaces-temps courbés. Comprendre les propriétés de 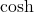et 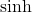peut aider à résoudre des problèmes complexes liés à la courbure de l’espace-temps.
3. Thermodynamique et Statistique :Les fonctions hyperboliques sont également présentes dans les distributions statistiques en physique statistique et en thermodynamique, telles que les distributions de Boltzmann et les fonctions de partition. La manipulation de ces fonctions peut conduire à des insights sur les comportements thermodynamiques des systèmes.

Une Porte vers de Nouvelles Découvertes

Notre exploration de cette somme infinie n’est qu’un exemple parmi tant d’autres de la beauté et de la profondeur des mathématiques. En démêlant les complexités des séries infinies, nous découvrons des relations cachées et des structures élégantes qui peuvent nous inspirer à chercher plus loin et à explorer davantage.

Conclusion

La mathématique est une aventure sans fin, remplie de mystères à résoudre et de beautés à découvrir. Chaque problème résolu ouvre la porte à de nouvelles questions et à de nouvelles explorations. En apprenant à manipuler des séries infinies et à utiliser les identités mathématiques à notre avantage, nous nous armons des outils nécessaires pour naviguer dans ce vaste univers de connaissances.

Alors, chers lecteurs, continuez à explorer, à poser des questions et à chercher des solutions. Les mathématiques sont bien plus qu’un simple exercice intellectuel ; elles sont une fenêtre sur l’infini, une aventure à la découverte de la vérité et de la beauté cachées de notre monde.

Chapitre 9 : Bonus : Anecdotes et Petits Secrets sur Fibonacci et le Nombre d’Or

Pour conclure notre aventure mathématique, plongeons dans quelques anecdotes amusantes et peu connues sur Fibonacci et le nombre d’or. Ces histoires montrent à quel point ces concepts sont enracinés dans notre culture et notre histoire, bien au-delà des mathématiques pures.

Fibonacci : L’Homme Derrière les Nombres

1. Un Nom qui Reste :Le vrai nom de Fibonacci était Leonardo Pisano Bigollo. “Fibonacci” est un surnom dérivé de “filius Bonacci,” signifiant “fils de Bonacci.” Son père, Guglielmo Bonacci, était un marchand, et c’est grâce à lui que Fibonacci a voyagé et appris les systèmes de numération utilisés en Méditerranée.
2. Voyages et Découvertes :Fibonacci a voyagé à travers l’Afrique du Nord, l’Orient et l’Europe, où il a rencontré différentes méthodes de calcul. C’est en grande partie grâce à ses voyages qu’il a découvert le système de numération arabe, qui est beaucoup plus efficace que le système de chiffres romains utilisé en Europe à l’époque.
3. Le “Liber Abaci” :En 1202, Fibonacci publie son livre le plus célèbre, “Liber Abaci” (Le Livre de l’Abacus). Ce livre a introduit le système de numération arabe en Europe, expliquant comment les chiffres 0-9 peuvent être utilisés pour simplifier le calcul. C’est aussi dans ce livre qu’apparaît pour la première fois la suite de Fibonacci, dans le contexte d’un problème de reproduction de lapins.

Le Nombre d’Or : Une Proportion Mystique

1. L’Harmonie dans l’Art et la Nature :Le nombre d’or, 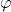, est souvent appelé la “divine proportion” en raison de sa présence récurrente dans la nature et l’art. Les spirales des coquillages, les galaxies, les tournesols, et même les proportions du corps humain suivent souvent la proportion dorée.
2. Léonard de Vinci et la Divine Proportion :Léonard de Vinci a utilisé le nombre d’or dans plusieurs de ses œuvres, y compris “La Cène” et “L’Homme de Vitruve.” Il a été présenté à cette proportion par son ami et mathématicien Luca Pacioli, qui a écrit un traité intitulé “De Divina Proportione,” illustré par Léonard.
3. Le Nombre d’Or dans l’Architecture :De nombreuses structures célèbres, comme les Pyramides de Gizeh et le Parthénon à Athènes, sont souvent citées comme utilisant le nombre d’or dans leurs proportions architecturales. Bien que les preuves historiques soient parfois discutables, l’idée que le nombre d’or confère une esthétique harmonieuse perdure.
4. L’Approximation Continue :Une des propriétés fascinantes de 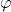est sa relation avec les fractions continues. Le nombre d’or peut être exprimé comme une fraction continue infinie :

Cette représentation montre la complexité et la beauté infinie du nombre d’or.

Des Mathématiques à la Culture Pop

1. Le Nombre d’Or dans les Livres et les Films :Le nombre d’or a capturé l’imagination de nombreux auteurs et réalisateurs. Il est souvent mentionné dans des œuvres de fiction pour ajouter une touche de mystère et de profondeur. Par exemple, dans le roman “Le Code Da Vinci” de Dan Brown, le nombre d’or joue un rôle central dans les énigmes que les personnages doivent résoudre.
2. Fibonacci dans les Cryptomonnaies :Les séquences de Fibonacci sont utilisées dans l’analyse technique des marchés financiers, y compris les cryptomonnaies. Les retracements de Fibonacci sont une méthode populaire pour prédire les niveaux de support et de résistance dans les graphiques de prix.

Un Avenir Prometteur

Les concepts de Fibonacci et du nombre d’or continuent d’inspirer et de captiver les esprits dans les domaines des mathématiques, de l’art, de la finance, et bien plus encore. En étudiant ces idées et en explorant leurs applications, nous continuons à découvrir de nouvelles connexions et à apprécier la beauté et l’harmonie de notre monde.