Pourton.info 
Quand les Maths rencontrent les Microbes
Les virus ne calculent pas, mais nous si ! Derrière chaque épidémie, il y a des chiffres, des modèles et des prévisions qui peuvent sembler aussi mystérieux que les créatures microscopiques elles-mêmes. Lorsque les mathématiques et la biologie se croisent dans le domaine des maladies infectieuses, nous pouvons commencer à dévoiler les secrets de la propagation virale et à trouver des stratégies pour la contenir. Armés de notre fidèle allié — les mathématiques — explorons comment la théorie des probabilités et les équations différentielles entrent dans cette bataille contre les bio-belligérants.
Imaginez que vous êtes dans une pièce avec une personne qui éternue. La probabilité que vous attrapiez le virus dépend de plusieurs facteurs, tous quantifiables. Pour les modéliser, les épidémiologistes utilisent des équations qui ressemblent à des recettes, sauf que, au lieu de cookies, elles nous donnent des prédictions sur l’infection. L’une de ces équations est la suivante :
Chaque symbole est un ingrédient clé dans notre recette épidémiologique :
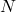représente le nombre de personnes dans la pièce.
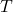est le temps pendant lequel les personnes sont exposées au virus.
mesure la concentration des particules virales dans l’air.
est le taux de renouvellement de l’air (ventilation).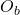
indique la quantité d’aérosols produit par la respiration ou la parole.
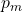représente l’efficacité du masque porté, réduisant la probabilité de transmission.
est le taux d’élimination des particules virales (par ventilation et filtration).
est le volume de la pièce.
Dans ce chapitre, nous allons démonter cette équation, pièce par pièce, pour comprendre comment chaque variable influence notre risque de tomber malade et comment les mathématiques peuvent nous aider à rester en sécurité.
L’Assemblée des Aerosols : Comment les Particules se Réunissent en Intérieur
La dynamique des aérosols dans un espace clos ressemble un peu à une danse sociale très animée — mais à une échelle microscopique. Les particules virales, une fois expulsées par un éternuement, une toux ou simplement en parlant, ne tombent pas juste par terre. Au lieu de cela, elles s’engagent dans une chorégraphie aérienne, poussées par les courants d’air, attrapées dans des tourbillons, et parfois, hélas, inhalées par un spectateur peu méfiant.
Pour comprendre la mobilité et la stabilité de ces particules dans l’air, nous pouvons utiliser une série d’équations qui décrit leur comportement en fonction de l’environnement. Le taux de ventilation et le volume de la pièce jouent des rôles cruciaux ici. Le modèle simplifié pour la dispersion des aérosols est donné par :
où 
est la concentration des particules à un moment donné 
, et 
est le taux de changement de cette concentration. Cette équation balance la production de nouveaux aérosols dans l’air et leur élimination via la ventilation et la filtration naturelle ou mécanique.
Pour ajouter un peu de piquant mathématique à notre plat, nous devons considérer que les particules plus petites peuvent rester en suspension plus longtemps que leurs homologues plus grandes, augmentant ainsi le risque de transmission par inhalation. La taille des particules est essentielle et peut être décrite par une fonction de distribution qui compte non seulement pour le nombre de particules mais aussi pour leur taille. Ainsi, nous avons :
où 
représente la distribution de la taille des particules à un temps , et 
est le rayon des particules. Les limites d’intégration, 
et 
, représentent respectivement les tailles minimale et maximale des particules en suspension.
Cette “danse” des aérosols n’est pas seulement une affaire de science — c’est un ballet dont les enjeux sont élevés, où chaque détail compte, de la ventilation à la vitesse de l’air. En ajustant ces variables, nous pouvons efficacement “chorégraphier” un environnement plus sûr et réduire la probabilité de transmission de maladies aériennes. Une performance où, espérons-le, les aérosols restent loin des voies respiratoires des invités !
Ventilation et Virulence : Le Duo Dynamique pour Diluer les Dangers
Si vous pensiez que les systèmes de ventilation étaient juste là pour maintenir votre confort, détrompez-vous : ils sont de véritables guerriers dans la lutte contre les maladies aéroportées. Imaginez un système de ventilation non pas comme un simple ventilateur, mais plutôt comme un super-héros du monde microscopique, armé de filtres et de flux d’air, combattant les envahisseurs invisibles.
Le taux de ventilation , combiné avec le volume de la pièce , détermine le taux de changement d’air, ou le nombre de fois que l’air dans la pièce est complètement remplacé par de l’air frais en une heure. Ce taux est crucial car il influence directement , notre taux de perte d’aérosols. L’équation de base pour le calcul de est :
où est mesuré en renouvellements d’air par heure. Plus cette valeur est élevée, plus les particules virales sont rapidement expulsées de la pièce, réduisant ainsi le risque d’inhalation.
Mais ne nous arrêtons pas là ! La filtration de l’air joue également un rôle clé. Les filtres, en fonction de leur classe MERV (Minimum Efficiency Reporting Value), peuvent capturer des particules de différentes tailles, y compris celles chargées de virus. Prenons par exemple un filtre avec une efficacité de filtration 
, le taux réel d’élimination des particules serait alors ajusté par :
Dans cette formule, représente la probabilité qu’une particule soit filtrée à chaque passage à travers le système. Cela nous montre que l’efficacité d’un système de ventilation n’est pas seulement question de volume d’air déplacé, mais aussi de la qualité de cet air après filtration.
Pour rendre cela un peu plus réel, imaginons une salle de classe où les risques de transmission doivent être minimisés. Si cette salle est équipée d’un système de ventilation mécanique de haute qualité, la concentration d’aérosols infectieux peut être réduite à des niveaux presque indétectables, permettant aux étudiants et aux enseignants de se concentrer sur Pythagore plutôt que sur les pathogènes.
Masques en Mission : L’Arithmétique derrière le Blocage des Balles Bactériennes
Si notre système de ventilation est le chevalier en armure brillante, pensez aux masques comme à nos boucliers fiables dans la bataille contre les invasions virales. Quand il s’agit de l’efficacité des masques, nous plongeons dans un monde où la filtration devient une affaire de pourcentages et de probabilités.
Pour quantifier l’impact des masques sur la réduction de la transmission des maladies, nous introduisons le facteur de pénétration du masque, , qui mesure la fraction des particules qui peut passer à travers le masque. L’efficacité du masque, donc, peut être exprimée comme 
, où un de 0.1 signifie que le masque filtre 90% des particules.
En termes mathématiques, l’impact des masques sur la concentration de particules virales dans l’air est modélisé par une modification de notre formule de base pour 
, en tenant compte de l’efficacité des masques portés par la source et le récepteur. La nouvelle équation devient :
Le terme 
souligne que la protection est fonction de l’efficacité des masques portés par la personne infectée et par la personne susceptible de l’être. Il s’agit d’une multiplication des probabilités, reflétant le fait que les masques doivent réussir deux “tests” : bloquer les particules virales à la fois à l’exhalation et à l’inhalation.
Pour illustrer cela avec une touche d’humour, imaginez que les particules virales sont des petits ninjas toxiques essayant de passer les portes gardées par deux vigiles (les masques). Si chaque vigile a 90% de chances de stopper un ninja, la probabilité qu’un ninja passe les deux vigiles est seulement de 1%. Voilà la beauté de la multiplication des probabilités en action !
Conclusion Calculée : Ce Que les Nombres Nous Disent Sur le Futur de Nos Fréquentations
Au terme de notre voyage à travers les équations et les aérosols, nous avons appris comment les mathématiques ne sont pas juste des abstractions mais des outils essentiels pour naviguer dans notre monde, parfois invisible, toujours important. L’arithmétique derrière les masques, les particules, et la ventilation nous montre que chaque facteur compte et que chaque précaution a son importance dans la danse délicate de la prévention de la maladie.
Considérons maintenant comment appliquer ces principes mathématiques dans notre quotidien. La compréhension de ces modèles nous offre une carte pour réduire les risques dans nos espaces de vie et de travail. Que ce soit en ajustant le taux de ventilation dans notre bureau, en choisissant judicieusement le type de masque à porter, ou simplement en évaluant le risque d’un rassemblement, les mathématiques nous donnent le pouvoir de prendre des décisions informées.
En rappelant notre équation initiale :
nous voyons que réduire (le nombre de personnes), augmenter (le volume de la pièce) ou (le taux de renouvellement de l’air), et améliorer (l’efficacité des masques) sont tous des moyens efficaces de diminuer , le risque d’infection. Cela illustre une vérité fondamentale : bien que nous ne puissions pas toujours voir les virus, nous pouvons contrôler notre environnement pour minimiser leur impact.
Finalement, rappelons-nous que les mathématiques sont une langue universelle qui nous aide à clarifier le chaos du monde naturel. Alors que nous continuons à naviguer dans cette ère de pandémie et au-delà, armés de nos calculatrices et de notre savoir, nous pouvons espérer garder une longueur d’avance sur nos minuscules adversaires microbiens. Parce qu’au final, dans le grand calcul de la vie, chaque détail compte—et chaque équation est une étape de plus vers la compréhension.
